Donalda Knuta, dobitnika Tjuringove nagrade 1974. godine, smatraju jednim od najvećih naučnika u kompjuterskim naukama. Njegovo grandiozno trotomno delo The Art of Computer programming predstavlja neku vrstu biblije u računarskim naukama. On ne samo da komponuje već i u slobodno vreme svira orgulje koje je sam dizajnirao.

Prof. dr Miodrag Petković
„Programiranje je vrsta umetničke forme
kao što su to poezija ili muzika” (Computer programming
is an art dorm, like the creation of poetry or music) Donald Knut
Donald Knut je rođen 1938. u Milvokiju (SAD). Doktorirao je matematiku 1963. na Kalifornijskom institutu za tehnologiju (Pasadena), a posle kratkog boravka na ovom prestižnom univerzitetu 1968. godine dobio je poziciju profesora na Univerzitetu Stenford. Na lični zahtev otišao je prevremeno u penziju u zvanju profesora emeritusa 1998. da bi mogao da se posveti pisanju knjiga. Smatra se jednim od najvećih naučnika u kompjuterskim naukama.
Ono što Donalda Knuta razlikuje od
drugih naučnika jeste univerzalnost
i originalnost u svemu što radi.
Njegovo grandiozno trotomno delo The Art of Computer programming predstavlja neku vrstu biblije u računarskim naukama. Knut je dao veliki doprinos u razvoju kompajlera, softverskog alata, analize algoritama, kreiranju revolucionarnog programa za procesiranje teksta TEX itd. Korišćenje ovog tekst-procesora i pratećeg softvera METAFONT za dizajniranje slova, znakova i simbola unelo je pravu revoluciju u publikovanju naučnih časopisa i knjiga (naročito u matematici i donekle u fizici), gotovo u rangu Gutenbergove štampe. Broj matematičkih časopisa se uvišestručio, finalni radovi mogu da se obrađuju na kućnom kompjuteru, a pritom se još dobilo na estetici teksta i formula.
Ono što Donalda Knuta razlikuje od drugih naučnika jeste univerzalnost i originalnost u svemu što radi. Njegovo jedinstveno predznanje uključuje ljubav za jezike i gramatiku, ogromno znanje matematike, snažnu vizuelnu estetiku, želju za razumljivim i preciznim izražavanjem i ljubav za programiranje. U svojoj dugogodišnjoj karijeri, osim velikog doprinosa u kompjuterskim naukama, matematici i algortmima, Knut je našao vremena za pisanje o različitim temama, kao što su vavilonski algoritmi, biblijski psalmi i romani. Knjiga Surreal Numbers iz 1974. govori o dvojici maloletnih drugova koji su napustili školu da bi se bavili razvojem sopstvenog matematičkog sistema.
Knutova velika ljubav je muzika; on ne samo da komponuje već i u slobodno vreme svira orgulje koje je sam dizajnirao. Neki se pitaju da li takav čovek može zaista biti samo jedna osoba?
On je počasni doktor na velikom broju
univerziteta širom sveta i član
Nacionalne akademije nauka SAD,
Kraljevskog društva Engleske, Francuske
akademije nauka i Ruske akademije nauka.
Donald Knut je rano počeo sa osvajanjem nagrada. Kada je bio u osmom razredu, lokalni proizvođač slatkiša je sponzorisao takmičenje u sastavljanju najvećeg broja reči koje se mogu dobiti od slova fraze „Ziglerova džinovska čokolada” (Ziegler`s Giant Bar). Mladi Donald je sam pronašao otprilike 4.500 reči, dok su sudije imale oko 2.500 na svojoj kontrolnoj listi, pa je dobio prvu nagradu (teelvizor) i dovoljno čokolada za celu školu.

Huverova kula u kampusu Univerziteta Stenford (M. Petković)
Tokom svoje karijere Knut je dobio mnoga javna priznanja i nagrade, uključujući najveću iz računarskih nauka, Tjuringovu nagradu (1974) i Nacionalnu medalju nauka od predsednika Džimija Kartera (1979). On je počasni doktor na velikom broju univerziteta širom sveta i član
Nacionalne akademije nauka SAD, Kraljevskog društva Engleske, Francuske akademije nauka i Ruske akademije nauka. On se prema tim zaslugama odnosi sa izvesnom ravnodušnošću, pa mu pehar koji simbolizuje Tjuringovu nagradu služi za držanje voća.
Matematika slova „S”
Sedamdesetih godina 20. veka postojao je veliki jaz između matematike i kompjuterskih nauka. Bilo je uobičajeno da se programi pišu i doteruju sve dok ne prorade. Donald Knut i njegov stariji kolega Edger Dijkstra prvi su počeli da koriste matematički aparat da dokažu valjanost i efikasnost programa, što je bila radikalna novina.
Svakoj istraživačkoj temi uvek je pristupao s karakterističnom temeljitoošću. Na primer, napisao je rad pod nazivom ,,Slovo S” u kome analizira matematički oblik ovog slova tokom vekova i objašnjava svoj višednevni napor da nađe jednačinu koja daje zadovoljavajući oblik. Studentima je često zadavao seminarske radove iz programiranja s neobičnim i originalnim temama, kao što su određivanje prvih 20 miliona decimala broja π, nalaženje zadatog niza slova u rečiima, omeđivanje najveće površi pomoću 12 standardnih pločica pentamina, nalaženje najdužeg nepresecajućeg puta figure skakača na šahovskoj tabli dimenzije n×n itd.
Ovakve teme su, po pravilu, bile izazovne i imale istraživački karakter, tako da su zahtevale kreativan i samostalan rad u kreiranju algoritama i programskoj realizaciji. Takva vrsta problema neretko je značila za studenta uvođenje u naučna istraživanja. Jedan od poznatijih problema kojim je motivisao svoje studente jeste skakačeva turneja ili krug na šahovskoj tabli. To je putanja skakača kojom on posećuje svako polje šahovske table jednom i samo jednom, a zatim se vraća na polazno polje. Putanja skakača je izlomljena zatvorena linija koja se sastoji od duži što spajaju centre odskočnog i doskočnog polja. Jednu varijantu skakačevog kruga na šahovskoj tabli predložio je Amerikanac L. D. Jardbrou jula 1968. U časopisu Journal of Recreational Mathematics.
· Odrediti najdužu putanju skakača na šahovskoj tabli 8h8 takvu da skakač ne sme posetiti nijedno polje više nego jednom. Na tom putu postoje stroga ograničenja da putanja ne sme da seče samu sebe.
Problem je prilično težak i preporučuje se korišćenje kompjuterskog programa.
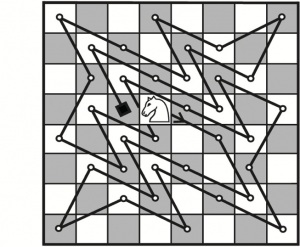
Najduži nepresecajući put skakača na tabli 8 × 8
Autor ovog članka imao je čast da o pomenutoj skakačevoj putanji vodi diskusiju s profesorom Knutom koji je, između ostalog, napomenuo da je Jardbrou samo ponovo otkrio ovaj problem koji je 30 godina ranije komponovao poznati šahovski kompozitor T. R. Dosan (Dawson). U slučaju najdužeg nepresecajućeg puta skakača na standardnoj šahovskoj tabli 8 × 8 Knut je pomoću tzv. backtrack kompjuterskog programa pronašao četiri osnovna rešenja. Da bi se došlo do njih, bilo je potrebno ispitati 3.137.317.289 slučajeva. Rešenje prikazano na gornjoj slici dato je u knjizi Mathematics and Chess (Dover Book, New York, 1997) autora ovog članka.
Po Donaldu Knutu, pesma dužine N
s refrenom smanjuje njenu prostornu
kompleksnost na cN, gde je c < 1.
Pomenimo još jedan vrlo interesantan Knutov problem koji je u svoje vreme izazvao burnu diskusiju u časopisu Journal of Recreational Mathematics. U zadatku se koristi komplet pentamino figura prikazan na donjoj slici. To su ravanske figure koje se sastoje od pet jediničnih kvadrata sastavljenih na različite načine preko zajedničkih ivica. Zbog sličnosti, obično se predstavljaju velikim slovima latinice U, V, T, L, Y, N, X, P, W, F, Z, I.
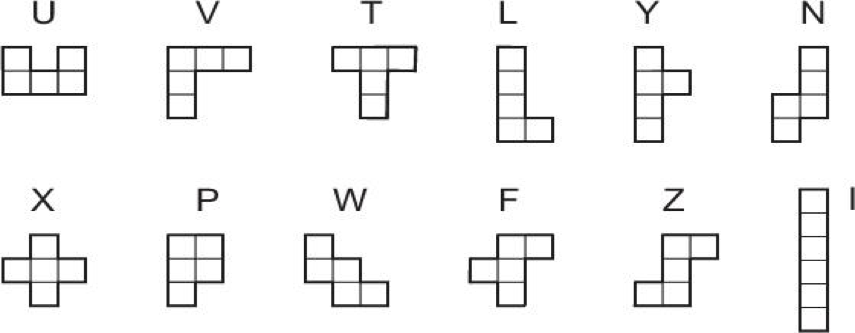
· Koristeći komplet od 12 pentamina napraviti ogradu bilo kog oblika koja će potpuno ograditi oblast maksimalne površine. Duž čitave svoje dužine ograda mora imati širinu od bar jednog kompozitnog kvadrata 1 × 1, drugim rečima, figure se ne smeju spajati temenima već samo ivicama.
Prostornost pesama
Pentamino-ograda koja okružuje maksimalnu površinu od 128 jediničnih kvadrata prikazana je na donjoj slici. Rešenje je dao sam Donald Knut. Mada rešenje nije jedinstveno, on je pokazao da broj od 128 kvadratnih jedinica ne može biti nadmašen.

Pentamino ograda najveće površine

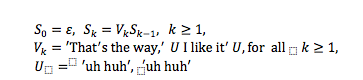
Verovatno je velikom broju čitalaca poznata igračka pod imenom Mastermind koju na specijalnoj tabli igraju dva igrača; jedan koji zadaje tajnu šifru kombinacijom 4 boje (od 6 raspoloživih) i drugi koji pokušava da u što manjem broju pogađanja otkrije šifru uz delimičnu pomoć šifranta (postoji 64 = 1206 mogućih pozicija).
Sedamdesetih godina 20. veka ova igračka bila je veoma popularna i prodata je u preko 50 miliona primeraka. I ovde je Donald Knut umešao prste. Godine 1977. je načinio algoritam koji omogućuje da se zadata šifra otkrije u najviše pet pokušaja.









