Božanski algoritam (God’s algorithm) je pojam koji je nastao u diskusiji o optimalnom rešenju Rubikove kocke, ali se može primeniti i na druge zadatke ili igre kombinatornog tipa. Odnosi se na algoritam koji, sledeći pravila igre, daje rešenje u najmanjem broju sukcesivnih poteza koji se ne može smanjiti. Ovaj broj zove se Božanski broj (God’s number) i njegovo nalaženje je izazovan ali po pravilu vrlo težak problem koji najčešće zahteva primenu kompjutera, a pored toga često i više godina rada.

Prof dr Miodrag Petković
Autor ovog priloga se sa velikom nostalgijom seća stare GALAKSIJE. Tada nije bilo interneta i ovaj mesečnik je u pravom smislu bio prozor u svet nauke. Komplet svih brojeva je jedna od najdragocenijih zbirki u mojoj biblioteci. Osamdesetih godina prošlog veka sa mojim kolegom sa Elektronskog fakulteta u Nišu Ljubišom Kocićem par godina uređivao sam rubriku pod nazivom Između igre i matematike, koja je za cilj imala popularizaciju matematike. Od mnogobrojnih priloga u sećanju mi je najviše ostao jedan zadatak postavljen pre više od 100 godina a koji sam postavio čitaocimaGALAKSIJE. Pre nego što objasnim razlog za ovaj neizbrisiv utisak, smatram da je potrebno objasniti pojam Božanskog brojakoji se pominje u naslovu priloga.
Božanski algoritam (God’s algorithm) je pojam koji je nastao u diskusiji o optimalnom rešenju Rubikove kocke (koju ćemo pomenuti u drugom delu ovog priloga), ali se može primeniti i na druge zadatke ili igre kombinatornog tipa. Odnosi se na algoritam koji, sledeći pravila igre, daje rešenje u najmanjem broju sukcesivnih poteza koji se ne može smanjiti. Ovaj broj zove se Božanski broj (God’s number) i njegovo nalaženje je izazovan ali po pravilu vrlo težak problem koji najčešće zahteva primenu kompjutera, a pored toga često i više godina rada. Ponekad se ovaj pojam upotrebljava za maksimalan broj poteza ukoliko je cilj igre /zadatka ostvarivanje maksimalnog broja poteza (videti primer 3).
Treba naglasiti da problemi predstavljeni u ovom prilogu i njima slični nisu ni nevažni niti su samo zabava i gubljenje vremena, kako neki naučnici žele to da predstave. Da je to slučaj, tada bi bilo bez ikakvog značaja i izračunavanje broja π više od 100 decimala (broj dovoljan za bilo kakva izračunavanja u poznatom univerzumu), čuveni problem četiri boje, slično je i sa Keplerovim problemom o najgušćem pakovanju sfera, kompjuterskim programima za igranje šaha i drugih igara, itd. Ipak, naučnici širom sveta, pre svega matematičari i programeri, su veoma posvećeni ovim problemima i rade na njihovom rešavanju i više godina. Razlog je jednostavan:proces rešavanja koji zahteva nove algoritme, nove teorije i nove tehnike veoma je koristan u oblasti veštačke inteligencije, za testiranje softvera i hardvera računara i još mnogo toga.
A evo i teksta pomenutog zadatka.
U vreme predsedničkih izbora u SAD 1908. godine veliki uspeh kod publike imala je zagonetka-igračka prikazana na slici.
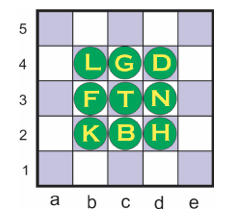
Svaka figura na ploči 5 x5 predstavlja predsedničkog kandidata: L– Lafolet, G– Grej, D– Džonson, F– Ferbanks, T – Taft, N– Noks, K – Kenon, B– Brajen, H– Hogs. Potrebno je sa table udaljiti osam kandidata, ostavivši samo jednog – pobednika na centralnom polju. Ovaj postupak treba obaviti u što manjem broju poteza. Potez se sastoji ili od jednog premeštanja figure na susedno polje gore, dole, levo, desno ili dijagonalno u sva četiri pravca (kao potez kralja u šahu – pretpostavljamo da svi znate bar najosnovnija pravila u šahu), ili u seriji skokova jedne iste figure pri čemu se u svakom skoku preskače samo jedna figura i to u bilo kojem od pravaca: gore, dole, levo, desno ili dijagonalno. Svaka preskočena figura odmah se skida sa table.
Skoro šezdeset godina se smatralo da je minimalan broj poteza za rešavanje ove zagonetke-igračke jednak pet. To rešenje je dao najveći i najslavniji sastavljač matematičkih zagonetki, logičkih zadataka, rebusa i šahovskih problema ikada, čuveni Sem Lojd(1841-1911). Pored Lojdovog rešenja postoji veliki broj rešenja u 5 poteza. U jednom od njih, na primer, Taft u prvom potezu može eliminisati čak šest kandidata, Noksa, Džonsona, Lafoleta, Kenona, Brajena i Greja (ovim redom), međutim, zadatak se na ovaj način ne može rešiti u manje od 5 poteza.
Šezdesetih godina dvadesetog veka ustanovljeno je da se zadatak o predsedničkim kandidatima može rešiti u samo 4 poteza. Postupak je sledeći (ali ne i jedini):
- Taft preskače redom Noksa, Džonsona, Lafoleta i Kenona;
- Hogs preskače Brajena;
- Grej preskače Ferbanksa i Hogsa;
- Taft preskače Greja i stiže u centar table.
Ovo rešenje naveo sam u pomenutoj rubrici u članku o zagonetkama-premeštaljkama u naučno-popularnom časopisu GALAKSIJA, broj 122 (1982). Samo mesec dana kasnije u redakciju časopisa stigla su četiri rešenja ovog problema – u samo tri poteza!
Ovaj događaj bio je još jedan primer dugogodišnje optimizacije rešenja zadatog zadatka i finale u traženju minimalnog rešenja – svetski rekord je oboren i ne može se popraviti. To je značilo da je Božanski broj za opisanu zagonetku-premeštaljku konačno dobijen!
Vredno je pomenuti imena čitalaca koji su najzad, posle 74 godine od postavke problema, pronašli optimalno rešenje: Dragan Pejčić (Niš), Simon Černuta (Bovec), Bojan Pesek (Maribor) i Milovan Kovačević (Šid). Nije nikakvo čudo što su se među rekorderima našla i dva Slovenca, u to vreme GALAKSIJA se čitala širom tadašnje Jugoslavije i dostizala tiraž i do 80 000 primeraka po broju.
Evo rešenja (čitaoci koji žele sami da pokušaju da pronađu rešenje u 3 poteza mogu da preskoče sledeće redove) koje se, inače, bitno razlikuje od ranijih. U prva dva poteza nijedan kandidat nije eliminisan i oni služe za „postavljanje” kandidata u povoljan položaj za njihovu eliminaciju u trećem potezu:
- Grej se pomera gore-desno (na polje d5 prema šahovskoj notaciji);
- Brajen se pomera dole-levo(na b1);
- Taft preskače redom Noksa, Hogsa, Brajena, Kenona, Ferbanksa, Lafoleta, Greja i Džonsona, završavajući pobednički pohod u centru table!
Polazeći od ovog osnovnog rešenja mogu se dobiti i simetrična rešenja, a i ona dobijena kao lik u ogledalu.
Dajemo još nekoliko Božanskih brojeva koji se odnose na dobro poznate primere.
Primer 1: Rubikova kocka
Rubikova kocka je 3D kombinatorna zagonetka koju je 1974.godine kreirao mađarski skulptor i profesor arhitekture Erne Rubik. Procenjuje se da je ova vrlo popularna igračka koja je osvojila svet dosad prodata u 350 miliona primeraka. Sastoji se od 26 malih kocki obojenih u 6 različitih boja i mehanizma u centru kocke za njihovu rotaciju. Cilj igre je da se rotacijama malih kocki velika kocka dovede u položaj (nazvan položaj istobojnih strana) u kome će svaka od 6 strana Rubikove kocke biti iste boje. Pomenimo da Rubikova kocka ima svoje mesto i u matematici, gde elementi tzv. grupe Rubikove kocke G(.) predstavljaju poteze mini-kocki.

Matematičari su izračunali da je ukupan broj pozicija koji može da zauzme Rubikova kocka broj koji se piše sa 19 cifara (deset milijardi milijadi). Ako se pretpostavi da se do svake pozicije može doći za 1 minut, da bi se realizovale sve pozicije bilo bi potrebno 82 000 milijardi godina! Ovako veliki brojevi stavili su matematičare i programere pred velike probleme u njihovom pokušaju da nađu minimalan broj poteza (Božanski broj) koji je dovoljan da se kocka složi polazeći od proizvoljne početne konfiguracije.
Najzad, godine 2010, Tomas Rokicki i njegov tim su došli do Božanskog broja: za slaganje Rubike kocke dovoljnoje 20 rotacija za bilo koju početnu poziciju. Korišćen je veliki broj vrlo moćnih Guglovih računara koji su radili neprestano nekoliko nedelja. Naravno da se u nekim vrlo povoljnim uslovima Rubikova kocka može složiti i u manjem broju poteza ali, s druge strane, postoje početne pozicije koje zahtevaju ne manje od 20 rotacija.
Uvek kada se govori o Rubikovoj kocki, neizbežno pitanje je koliki je svetski rekord u brzini u slaganju kocke. Trenutno ovaj rekord iznosi neverovatnih 3,47 sekundi a postavio ga je Kinez Jušeng Du 15. novembra 2018. na turniru u kineskom gradu Vuhuu 2018.
Primer 2: Hanojska kula
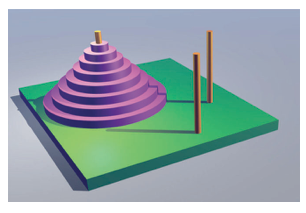
Hanojska kula je veoma poznata i popularna matematička zagonetka-premeštaljkakoju je izumeo franciski matematičar Eduar Lika 1883. godine. Sastoji se od 3 vertikalna klina postavljena na ploču i izvesnog broja diskova raličitih veličina. U početnom položaju diskovi su postavljeni tako da se manji disk uvek nalazi iznad većeg (kao na slici)
Diskovi se mogu prebacivati (po jedan u svakom potezu) sa jednog klina na drugi na takav način da je u bilo kom trenutku na bilo kom klinu manji disk uvek iznad većeg. Zadatak se sastoji u tome da se svi diskovi sa kule (klin sa diskovima u početnom položaju) prebace na neki od druga dva klina.
Pitanje: koliki je najmanji broj poteza potreban za prebacivanje diskova?
Minimalan (Božanski) broj je 2n-1 poteza. Ovaj broj bio je poznat i pre sto godina, ali on se odnosio na tzv. rekurzivni postupak pri prebacivanju diskova, bez dokaza da je ovaj postupak zaista i optimalan. Prvi korektan matematički dokaz dao je D. Vud u svom radu iz 1981, pri čemu je dokazao da je rekurzivni postupak istovremeno i optimalan.
Primer 3: Nepresecajuća skakačeva putanja
Skakačeva zatvorena putanja ili skakačev krug je čuveni klasičan problem na šahovskoj tabli 8 x8 (poznat još u 9. veku) kojim su se bavili i vrhunski svetski matematičari kao što su Ojler, Vandermond, Ležandr, De Muavr, De Monmor i drugi. To je putanja skakača kojom on posećuje svako polje šahovske table jednom i samo jednom, a zatim se vraća na polazno polje.
Jednu varijantu skakačeve putanje predložio je Amerikanac T. R. Dosan 1938. godine. Kao i kod uobičajenog skakačevog kruga, skakač ne sme posetiti nijedno polje više nego jednom. Pri ovom putu postoje stroga ograničenja: putanja ne sme da seče samu sebe. Lako se pokazuje da pod ovim ograničenjima skakač ne može posetiti sva polja šahovske table. Odavde proizilazi sledeći zadatak: Koliko najviše polja na šahovskoj tabli može da obiđe skakač (računajući i polazno polje) a da putanja ne sme da seče samu sebe?
Rešenje ovog problema u 35 poteza (36 polja) dao je D. Jardbrou u časopisu Journal of Recreational Mathematics 1968, ali bez dokaza o optimalnosti rešenja. Donald Knut, profesor Univerziteta u Stenfordu i jedan od najvećih svetskih naučnika iz oblasti kompjuterskih nauka, dao je kompletno rešenje ovog veoma teškog problema osamdesetih godina dvadesetog veka uz pomoć kompjutera. Koristeći backtrack algoritam, Knut je našao da postoje samo 4 osnovna rešenja do kojih se može doći ispitivanjem 3 137 317 289 slučajeva. Maksimalan broj poteza je 35 (36 polja) i on se ne može prevazići. Prema tome, u ovom primeru Božanski broj je 36.
Ispostavilo se da je Jardbrouovo rešenje bilo u potpunosti prihvatljivo.
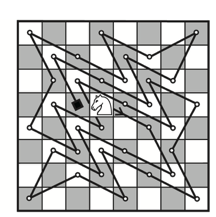
Ovo rešenje je navedeno u mojoj knjizi Mathematics and Chess koju je publikovao poznati izdavač Dover Publication iz Njujorka 1997. godine. To je bila i prva knjiga ikada napisana na engleskom jeziku koja kombinije osobine matematike i šaha u cilju sastavljanja izazovnih problema i zagonetki; i dan-danas se prodaje putem interneta (Amazon, Barnes & Noble).








