ČUVENI PENTIUM-ov BAG

Određivanje tzv. Brunove konstante koja se javlja u Teoriji prostih brojeva nije, samo po sebi, naročito važan problem. Međutim, njeno izračunavanje dovelo je do saznanja da i računari nisu bezgrešni. Tomas Najsli, matematičar sa malog Linčburg koledža u Virdžiniji (SAD), odredio je 1993. vrednost Brunove konstante s tačnošću do osmog decimalnog mesta. Ovaj poduvat nije toliko interesantan koliko jedna druga činjenica: tokom svojih kompjuterskih proračuna Najsli je naišao na više grešaka, koje je uočio samo zato što ih je radi sigurnosti izvodio na više različitih računara. Najveća greška koju je tom prilikom uočio bio je čuveni Pentium-ov bag.

Prof. dr Miodrag Petković

Povremeno će se u ovoj rubrici u pojavljivati zanimljivi prilozi iz sveta matematike koji uključuju interesantne matematičke formule, događaje iz sveta matematike i života velikih matematičara, kao i elementarne ali intrigantne i izazovne zadatke za čije rešavanje je dovoljno srednjoškolsko znanje matematike. Većina ovih priloga, i još matematičkih priča i zanimljivosti može se naći na sajtuwww.miodragpetkovic.com , autora ovih priloga (opcije teme u meniju).

Prosti brojevi (brojevi koji su deljivi jedino s brojem 1 i sami sa sobom) često se javljaju kao uzastopni neparni brojevi, kao što su 3 i 5, 11 i 13, 17 i 19 itd. Takvi prosti brojevi nazivaju se prostim blizancima. Trenutno (godina 2020.) najveći prosti blizanci su

koji imaju više od 388.342 cifara svaki. Skoro svake godine rekordi ove vrste se obaraju pomoću računara. Mada se pretpostavlja da blizanaca ima beskonačno mnogo, ova hipoteza još nije dokazana. Interesantno je da se ona pominje u filmu The Mirror Has Two Facesu kome profesor matematike, koga igra Džef Bridžis, objašnjava ovu hipotezu profesorki književnosti koju igra Barbra Strejsend.

Godine 1919. norveški matematičar Vigo Brun dokazao je da, ako sabiramo recipročne vrednosti uzastopnih blizanaca, suma će težitii jednoj određenoj vrednosti, danas poznatoj kao Brunova konstanta:

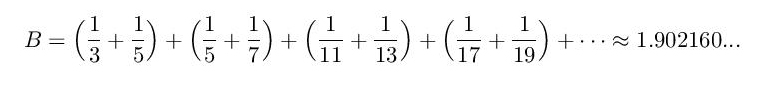
(čak i da ih ima beskonačno mnogo). S obzirom na poznatu činjenicu da suma recipročnih vrednosti prostih brojeva 1+1/3+1/5+1/7+1/11+… divergira ka beskonačnosti (ovo je dokazao Ojler još u 18. veku), konačna suma blizanaca je zaista impresivna. Interesantna je i osobina da se osim prvog, svi parovi blizanaca javljaju u obliku(6n-1,6n+1).

Brunova konstanta i njeno određivanje nije, samo po sebi, naročito važan problem. Međutim, njeno izračunavanje dovelo je do saznanja da i računari nisu bezgrešni, misli se pre svega na dizajniranje i konstrukciju njihovog hardvera. Tomas Najsli, matematičar s malog Linčburg koledža u Virdžiniji, odredio je 1993. vrednost Brunove konstante s tačnošću do osmog decimalnog mesta, B=1.90216058. Ovaj poduvat nije toliko interesantan koliko jedna druga činjenica: tokom svojih kompjuterskih proračuna Najsli je naišao na više grešaka, koje je uočio samo zato što ih je radi sigurnosti izvodio na više različitih računara. Najveća greška koju je tom prilikom uočio bio je čuveni Pentium-ov bag. Na najnovijem procesoru Pentium firme „Intel”, koji se na tržištu pojavio 1993. i bio odmah prodat u milionima komada, došlo je do neobične greške u potprogramu za množenje, tako da, na primer, zbir

1/824633702441+1/824633702443

(zbir recipročnih vrednosti prostih brojeva-blizanaca) nije bio dobro izračunat; rezultat nije bio tačan na 19 decimala, kako je potrebno i kako je obećano, već samo na 9 decimala. A to je dramatično loše ako sabiramo mnogo brojeva i pritom želimo da sprečimo akumulaciju grešaka. Ovo je bila katastrofa za „Intel” koji je morao ponovo da projektuje čip i da ga zameni na milionima mesta.

Katastofa je tim pre bila veća što je bila praćena brukom jer su u „Intelu” i sami prethodno otkrili grešku, ali su je prećutali. Ova greška i zamena ispravnim čipovima koštala je kompaniju skoro 500 miliona dolara.

U konkretnom slučaju problem je bio u aritmetičkoj jedninici Pentium procesora. Da bi se povećala brzina izračunavanja, korišćene su gotove tablice sa unapred izračunatim vrednostima elementarnih funcija za neke opsege vrednosti argumenata (lookup table). Ove tablice podsećaju delimično da davno korišćene logaritamske tablice ili tablice trigonometrijskih funkcija. Od 1066 ulaznih podataka, koliko je trebalo da sadrži lookuptablica konkretnog Pentium procesora, nedostajalo je 5 podataka, što je u nekim (istina, vrlo retkim) slučajevima dovodilo do toga da je procesor vraćao nedovoljno tačne rezultate.

Na ovom mestu trebalo bi reći da je dizajniranje efikasnog i pouzdanog harvera ili sofvera riskantan zadatak. Poznato je više bagova o kojima se u literaturi dosta diskutovalo. Čak iako je aritmetika bez nedostataka, ponekad (mada vrlo retko) dolazi do čudnog ponašanja, uglavnom kod numeričkih problema koji su istinski vrlo teški i loše uslovljeni. Ovo nije iznenađujuće: preslikavanje neprekidnog skupa realnih brojeva na konačan diskretan skup (kakav imaju kompjuterske aritmetike s pokretnom tačkom) ne može da prođe bez ikakvih problema.

U nastavku dajemo nekoliko poznatih bagova pomenutog Pentium procesora prve generacije:

– Aritmetička jedinica za deljenje u prvoj verziji procesora realizovanog 1994. godine nije idealno funkcionisala. U ekstremno retkim slučajevima, ona bi pri deljenju davala samo tri tačne decimalne cifre. Na primer, rezultat izračunavanja 8391667/12582905iznosio je 0.666869…umesto 0.666910…

– Programski paket Maple, verzija 7.0, kada je izračunavao 1001!/1000!, davao bi 1 umesto 1001 (podsećamo, n! označava proizvod svih prirodnih brojeva od 1 do n).

– Rezultat izračunavanja 850 x 77.1 (= 65535) pomoću ranijih verzija Excel-a 2007 iznosio je 100001. Greška je nastala pri konverziji binarnog u decimalni kod.

– Windows Calculator i Microsoft Excel u Windows-u 95/98 su, umesto tačne vrednosti (u aritmetici dvostruke preciznosti), pri deljenju4,195,835/3,145,727 (= 1.333820449136241002…),davali rezultat 1.333739068902037589, kod koga su sve podvučene cifre pogrešne.

Kad već govorimo o nesavršenostima kompjuterskog hardvera (koje se iz generaciju u generaciju otklanjaju u priličnoj meri), neizbežno je pomenuti kako je jedna obična konverzija iz jednog brojnog sistema u drugi na računaru ograničenih mogućnosti dovela do velike katastrofe i ljudskih žrtava.

U izveštaju Generalnog kompjuterskog biroa SAD od 25. februara 1991. stoji da je raketni odbrambeni sistem Patriot, koji je dejstvovao u Dahranu (Saudijska Arabija), propustio da uđe u trag i presretne dolazeći irački projektil Skad. Skad je pogodio vojne barake i usmrtio 28 američkih vojnika. Računar koji je korišćen za upravljanje raketom Patriot bio je zasnovan na 24-bitnoj aritmetici, razvijenoj 1974.

Patriot prati svoje mete mereći vreme koje je potrebno radarskom zraku da se odbije od mete i stigne natrag. Vreme se zapisuje pomoću satnog sistema u desetinkama sekunde, ali se smešta u memoriju kao ceo broj. Da bi se omogućilo izračunavanje vremena praćenja, vreme je konvertovano u 24-bitni binarni broj sa pokretnom tačkom. Greške zaokruživanja pri konverziji vremena prouzrokovale su pomak u „oblasti dometa”, koji se koristio za praćenje meta. Služba projekta Patriot dobila je 11. februara 1991. podatke s terena i uočila pomak od 20% u oblasti dometa Patriot-a nakon što je sistem neprekidno radio 8 sati. Ovi podaci su ukazali na to da sistem nakon 20 uzastopnih sati rada više neće biti u mogućnosti da izvrši presretanje rakete Skad.

Vojni stručnjaci su odmah započeli rad na modifikovanom softveru koji bi vršio kompenzaciju netačnog izračunavanja vremena, ali su zamalo zakasnili. Dana 25. februara Alfa baterija, koja je štitila vazduhoplovnu bazu Dahran, već je bila u neprekidnim ratnim operacijama 100 sati. Netačno izračunavanje vremena prouzrokovalo je da sistem više nije mogao da prati dolazeće rakete Skad. Gornja tabela jasno pokazuje kako je s povećanjem vremena rada Patriot izgubio trag svojih meta. Brojevi dati u tabeli su tačni sa relativnom greškom od 2^{-20} u kompjuterskoj reprezentaciji broja 0,1 – konstante koja je korišćena za konvertovanje desetinki sekunde satnog mehanizma sistema u sekunde (2^{-20} je relativna greška nastala odsecanjem 0,1 na 23 bita iza binarne tačke).

Kurioziteta radi, navodimo tri gotovo neverovatna primera u kojima pogrešni rezultati i neizvršeni zadaci nisu proizvod ikakve greške u programiranju ili hardveru kompjutera već su rezultat loše specifikacije. Na primer, satelit za ispitivanje klime planete Mars srušio se na nju septembra 1999. godine zbog katastofalne greške: jedan od timova koji su dizajnirali numerički softver podrazumevao je da je jedinica za dužinu metar, dok je drugi tim koristio stope. Vrlo slično desilo se juna 1985. godine kada se „svemirski šatl” loše pozicionirao u nastojanju da registruje odbijeni laserski zrak od vrha planine, ali se to nije desilo jer je unet podatak da je planina visoka 10.000 metara umesto tačnih 10.000 stopa. Pomenimo na kraju slučaj loše projektovanog mosta između Nemačke i Švajcarske (2004. godine) zbog toga što su dve zemlje koristile različite podatke o nadmorskoj visini na kojoj je most sagrađen.