U literaturi se za Toričelijevu trubu može naći i naziv Gavrilov rog. Ime asocira na arhangela Gavrila koji, duvajući u svoj rog, najavljuje Sudnji dan. Beskonačna površina je asocijacija na beskonačnu moć Boga. Deluje vrlo iznenađujuće da je površina Toričelije trube beskonačno velika, a da je njena zapremina ograničena i jednaka π jedinica. Osobe koje su pohađale standardni kurs matematičke analize na prvoj godini studija to mogu lako i da provere.

Prof. dr Miodrag Petković
Poduhvat da ubedite čitaoca da je matematika lepa nije lak s obzirom na dobro poznatu činjenicu da je matematika većini učenika srednjih škola i studentima (nematematičkih) fakulteta bila uvek jedan od najtežih predmeta. Možda i zbog toga što je nekima izgledala suvoparna, drugima previše egzaktna, bez mnogo prostora za improvizaciju. Autor se nada da će ovaj prilog koji sadrži nekoliko elementarnih ali veoma interesantnih matematičkih problema (između mogućeg i nemogućeg) sa neočekivanim, skoro paradoksalnim, rešenjima pobuditi radoznalost čitalaca jer je matematika onoliko zanimljiva koliko smo mi radoznali.
Toričelijeva truba
Najpoznatiji geometrijski objekat koji ima beskonačnu dužinu i površinu, ali konačnu zapreminu jeste Toričelijeva truba – objekat koji ima oblik trube i dobija se rotacijom krive funkcije f(x)=1/x za x∈[1,∞) oko x-ose, videti sliku 1. Ime je dobila po italijanskom fizičaru i matematičaru Evangelisti Toričeliju (1608-1647) koji je otkrio ovaj objekt sa pomenutim osobinama.
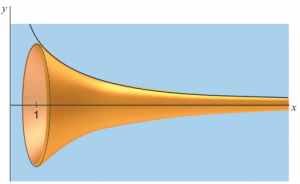
Slika 1 Toričelijeva truba
U literaturi se za Toričelijevu trubu može naći i naziv Gavrilov rog. Ime asocira na arhangela Gavrila koji, duvajući u svoj rog, najavljuje Sudnji dan. Beskonačna površina je asocijacija na beskonačnu moć Boga. Deluje vrlo iznenađujuće da je površina Toričelije trube beskonačno velika, a da je njena zapremina ograničena i jednaka π jedinica. Osobe koje su pohađale standardni kurs matematičke analize na prvoj godini studija to mogu lako i da provere. Zaista, površina tela (trube) dobijena rotacijom luka krive f(x)=1/x oko x -ose, ograničena s leva pomoću ravni x=1 , jednaka je:
Engleski filozof Tomas Hobs duhovito je primetio da ne samo da je ovo teško objasniti osobama koje se bave geometrijom ili logikom, već treba biti pomalo lud da bi se to shvatilo.
Za opisani problem vezan je jedan od najvećih paradoksa u matematici. Kako je zapremina trube konačna, potrebna nam je ograničena količina boje da bismo obojimo celokupnu (beskonačno veliku) površ Toričelijeve trube sipajući boju u trubu. Tako kaže matematika, ali u stvarnosti ne možemo napraviti beskonačno veliku Toričelijevu trubu, a takođe ni „čestice” boje ne mogu da budu manje od molekula.
Kocke princa Bavarskog
Početkom sedamnaestog veka princ Rupert postavio je vrlo interesantno i izazovno pitanje: Da li se kroz drvenu kocku može napraviti „tunel” kroz koji će proći veća kocka? Ako je ivica prve kocke 1, odrediti ivicu najveće kocke koja može da prođe kroz nju. Mnogi bi odgovorili (uključujući i univerzitetske profesore matematike) da je to nemoguće, ali princ Rupert je toliko bio uveren da postoji rešenje da je ponudio veliku opkladu.
Čuveni engleski matematičar Džon Volis bio je prvi koji je pokazao da je to moguće na primeru tunela čija je osa paralelna sa dijagonalom kocke. Ivica Volisove kocke imala je dužinu √6-√2≈1.03527 , što je veće od 1 i Rupert je dobio opkladu.
Sto godina kasnije ispostavilo se da Volisovo rešenje nije optimalno, tj. moguće je napraviti tunel pomoću veće kocke. Holandski matematičar Piter Nivland pokazao je 1793. godine da najveća kocka ima ivicu jednaku (3√2)/4≈1.0606601 . Konstrukcija i položaj ove kocke, poznate pod imenom Rupertova kocka, prikazana je na slici 2.
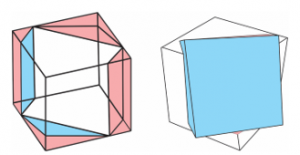
Slika 2 Rupertova kocka
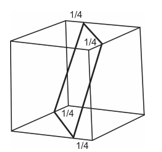
Slika 3 Najveći kvadrat u kocki
U bliskoj vezi sa Rupertovim problemom je konstrukcija najvećeg kvadrata koji ceo leži u jediničnoj kocki. Ivica najvećeg kvadrata jednaka je (3√2)/4≈1.0606601 i njegova konstrukcija se može videti na slici 3: potrebno je temena ovog kvadrata postaviti na razdaljini od 1/4 od odgovarajućih temena kocke. Ovaj kvadrat, „istisnut” u oba pravca ortogonalno na svoju početnu poziciju, pravi rupu kroz koju veća kocka (ivice (3√2)/4 , Nivlandovo rešenje) može da prođe kroz kocku ivice 1. Delovi jedinične kocke koji ostaju posle „bušenja ”tunela, formiraju dve trougaone prizme i dva nepravilna tetraedra, povezana pomoću tankih „mostova” u četiri ivice kvadrata. Od svojih šest temena, svaka prizma ima dva temena u dva susednsa temena kocke i četiri temena na susednim ivicama kocke na rastojanju od 1/4 od temena kocke.
Matematička konstrukcija Rupertove kocke je jasna, ali praktična demonstracija prolaženja veće kocke kroz manju pomoću modela (recimo, od papira) veoma je teška jer su ivice obe kocke vrlo bliske po veličini. Međutim, na internetu postoje vrlo uverljive i jasne kompjuterske video simulacije ovog „poduhvata”.
Savijanje mapa
Jedan od najneobičnijih nerešenih problema u kombinatorici, koji već više od jednog veka frustrira matematičare, jeste određivanje broja različitih načina za savijanje pravougaone „mape”. Postupci savijanja mapa se vrlo često javljaju u praksi, recimo pri sklapanju geografske ili topografske mape. Mapa se savija po „brazdama” duž vertikalnih i horizontalnih linija (isprekidane linije na slici 4) formirajući matricu m×n identičnih pravougaonika. Problem je predložio francuski matematičar Eduar Lika još 1891. godine, mada u literaturi postoje i ranije reference. Specijalan slučaj je mapa 1×n , tj. traka koja se sastoji od kvadrata. Ovaj partikularan problem se vrlo često naziva problem savijanja trake poštanskih maraka duž perforiranih ivica.
Slika 4 Savijanje mape
S pojavom računara matematičari i programeri su pokušali da problem reše pomoću specijalnih algoritama. Ispostavilo se da ne postoje efikasni algoritmi za rešavanje ovog problema jer vreme izračunavanja raste eksponencijalno, čak i u slučaju savijanja trake maraka. Broj različih načina savijanja trake T(n) za n=1,2,…15 dat je u tabeli 1, pri čemu simetrična („inverzna”) savijanja nisu računata.
Rekordi u pogledu dimenzije se sporo obaraju, uprkos porastu brzine mikroprocesora. Za kvadratnu mapu n×n broj savijanja K(n) dat je u tabeli 2 s napomenom da je trenutna gornja granica n=5 (2018). Možete li poverovati da se mapa dimenzije 3×3 može složiti na 1.368 načina?
Tabela 1 Broj T(n) različitih načina savijanja trake 1×n poštanskih mara

Tabela 2 K(n) različitih načina savijanja kvadratne mape n×n

Eksponencijalno iznenađujući
Procesi koji imaju eksponencijalni rast često dovode do veoma neočekivanih rezultata. U ovom delu navešćemo dva primera ove vrste.
Problem pšeničnih zrna na šahovskoj tabli. Ovaj problem se javlja u raznim pričama o nastanku šaha ali i o geometrijskoj progresiji. Prvi zapisi potiču iz Indije i stari su bar 1.000 godina. Na prvo polje šahovske table 8 x 8 stavlja se jedno pšenično zrno, na drugo polje dva, na treće 4, na četvrto 8 i tako dalje, na svako naredno polje dva puta više nego na prethodno (slika 5). Koliko ukupno ima zrna na šahovskoj tabli?
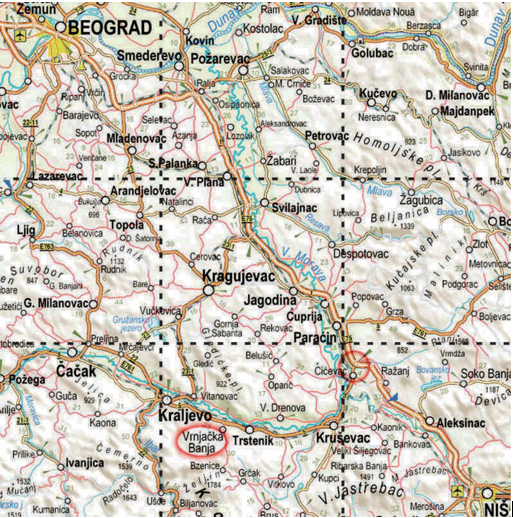
Većini čitalaca je verovatno poznato da je traženi broj zrna jednak zbiru geometrijske progresije:
ne daje uvid u količinu zrna, da li ona zauzimaju jednu sobu, olimpijski bazen ili…? Rezultat je krajnje iznenađujući: Ako bi svu količinu zrna smeštali u teretne vagone, a vagone poređali u jedan niz, dužina svih vagona bila bi 60 puta veća od razdaljine Zemlja-Sunce!

Slika 5 Zrna na šahovskoj tabli
Slika 6 Savijanje papira
Problem savijanja papira. Pretpostavimo da je papir pravougaonog oblika proizvoljno velikih dimenzija, debljine desetog dela milimetra, presavijen tačno na pola, a zatim da je dobijeni komad ponovo presavijen. Ako bi se process presavijanja papira izvršio 50 puta, kolika bi bila visina dobijene gomile papira?
Mnogi će na ovo pitanje odgovoriti metar ili dva, oni oprezniji rekli bi možda 1 kilometar, a najluđi odgovor mogao bi da bude, na primer, 100 kilometara. Međutim, tačan odgovor na ovo pitanje je krajnje zaprepašćujući: debljina papira iznosila bi oko 112 miliona kilometara, što je otprilike 3/4 razdaljine između Zemlje i Sunca.
Ovo je bila teorija. U praksi, pri savijanju papira mora se voditi računa o debljini presavijenog papira, koja raste takođe eksponencijalno jer se udvostručava pri svakom savijanju. Istovremeno, dužina papira se smanjuje svaki put duplo. Međutim, dužina papira l smanjuje se još i više zbog debljine presavijenog papira što, takođe, treba uzeti u obzir. Pretpostavimo da imamo papir dimenzije 20 cm×20 cm i da smo izvršili nekoliko savijanja i dobili uzorak debljine r. Pri sledećem savijanju sloj koji se savija mora da napravi polukrug poluprečnika r , ukupne dužine πr (slika 6). Ovaj utrošak materijala mora se uzeti u obzir jer se za toliko dodatno smanjuje dužina sloja. Zbog toga proces presavijanja neće više biti moguć kada dužina donjeg sloja bude manja od veličine polukruga.
Na primer, posle 6 savijanja debljina dobijenog sloja je jednaka 2^6∙0,1mm=6,4 milimetara. Kod sledećeg savijanja dužina donjeg sloja će se smanjiti dodatno za π∙6,4mm≈20,1mm, što je neophodno za presavijanje. Ako je originalni papir dimenzije 20cm ×20cm, dužina donjeg sloja nije veća od 20cm/2^3 =2,5cm . Ovaj primer pokazuje da će se u praksi zbog ograničene veličine datog papira savijanje završiti u konačnom broju koraka. Zaustavni broj koraka zavisi od dimenzija originalnog papira (pre početka savijanja) i njegove debljine. Brojni eksperimenti su pokazali da je osam savijanja gornja granica za papir dimenzije 20cm× 20cm.
Kolacov niz
Posmatrajmo generisanje sledećeg niza:
Izaberimo proizvoljan prirodan broj n .
1) Ako je n paran broj, delimo ga sa 2;
2) Ako je n neparan broj, množimo ga sa 3 i dodajemo 1.
Zatim se postupak nastavlja sa novodobijenim brojem.
Nemački matematičar Lotar Kolac (1910-1990) zapazio je još 1937. godine na velikom broju eksperimenata da posle izvesnog broja koraka ovako generisan niz daje broj 1. Postavio je i sledeće pitanje: Da li ovakvo generisanje brojeva uvek dovodi do 1, nezavisno od izbora početnog broja n? Godine 1952. Kolac je tim problemom „zarazio” svog hamburškog kolegu Helmuta Hasea, koji je sa svoje strane bacio u razmišljanje ceo Departman za matematiku Univerziteta u Sirakuzi (savezna država Njujork). Zbog toga se gornji niz ponekad zove Haseov algoritam, a često i Sirakuza problem. Tada je čak kružila priča da su Rusi promovisali ovaj problem da bi time paralisali matematička istraživanja u SAD, što im je navodno pošlo za rukom. Ovu glasinu možemo smatrati ironičnim komentarom hladnog rata koji je tada bio u jeku na relaciji SAD-SSSR.
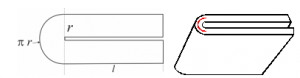
Primera radi, evo kako izgleda generisanje ako se krene od broja 17 (12 koraka):
Tomas Oliviera e Silva je, koristeći računar, testirao Kolacov niz i utvrdio da bilo koji startni broj manji od 5.4×〖10〗^18 daje 1, ali to ne potvrđuje hipotezu. Dakle, Kolacov problem i dalje ostaje otvoren. Pomenimo da je među brojevima manjim od 100 miliona nađeno da broj 63.728.127 zahteva najviše koraka, ukupno 949. Postoji interesantna igra za više učesnika zasnovana na Kolacovom nizu: svaki od učesnika bira broj iz dogovorenog intervala, recimo od 500 do 1.000, i pobednik je onaj koji u najviše koraka dođe do 1.
Problem četiri broja
Matematičar Benedikt Fridman utrošio je 10 godina rešavajući sledeći zadatak postavljen 1938. godine, koji na prvi pogled izgleda vrlo jednostavan.

Posle 10 godina rada, u januarskom broju časopisa Scripta Matematica (1948) pojavilo se Fridmanovo rešenje koje se odnosi na opštiji slučaj: Ako je broj komponenti m početnog vektora stepen broja 2 (tj. m=2^r), tada proces sa apsolutnim razlikama uvek dovodi do nula-vektora {0,0,…0}. Ako m nije oblika m=2^r, tada se u opštem slučaju ne dobija nula-vektor u konačnom broju koraka.
„Problem četiri broja” je samo specijalan slučaj kada je m=2^2 (r=2) . Ovaj zadatak i danas je vrlo aktuelan i atraktivan primer iz elementarne matematike koji mnogi matematičari često koriste da zabave i zadive svoje kolege, a i svoje učenike i studente.
Igra ciframa
Mnogi ljubitelji matematike bili su tokom četrdesetih okupirani popularnom igrom brojeva, proisteklom iz jednog problema u časopisu The American Mathematical Montly. Igra se sastojala u tome da se brojevi od 1 do 100 izraze pomoću 4 iste cifre, uz korišćenje jedino osnovnih aritmetičkih operacija (npr. 99+9/9=100).

Bilijarska „crna rupa”
Pedesetih godina dvadesetog veka nemačko-američki matematičar Ernst Štraus postavio je pitanje da li je moguće napraviti sobu čiji su zidovi prekriveni ogledalima tako da svetlost iz jedne tačke ne može dopreti u sve tačke unutar sobe, uzimajući u obzir da osvetljenje može dolaziti i posle refleksije od jednog ili više ogledala. Problem je ekvivalentan sledećem bilijarskom problemu: Da li se može konstruisati takav bilijarski sto da kugla udarena u nekoj (povoljno izabranoj) tački A nikad ne dođe u tačku B (tzv. „crna rupa”), makar se i beskonačno puta odbila od zidova?
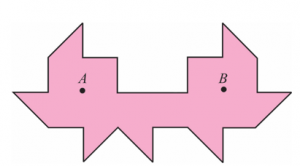
Slika 7 Prostorija sa „crnom rupom”
Ovaj zadatak nije bio rešen sve do 1995. kada je Džordž Tokarski smislip sobu s „crnom rupom” koja je imala 26 zidova. Dve godine kasnije D. Kastro je poboljšao ovaj rezultat i konstruisao sobu sa 24 zida prikazanu na slici 7. Ako se sveća stavi u tačku A, osoba koja stoji u tački B neće videti svetlost, uprkos refleksije staklenih ogledala postavljenih na zidove.
Neobičan troboj
Sledeća priča A. P. Herberta (Fat King Melon) iz 1927. govori o nekadašnjim vremenima kada su se nesuglasice, a posebno pitanja uvreda i odbrane časti, rešavale dvobojima. Za današnje vreme to je ne samo surov već i neshvatljiv način rešavanja sporova.
Jednog hladnog zimskog dana Sem, Bil i Don otišli su u lov na vukove. Posle dugog pešačenja šumskim stazama, na jednom proplanku ugledali su usamljenog vuka i svi istovremeno opalili iz svojih pušaka. Vuk je bio smrtno pogođen, a među lovcima je izbila svađa oko toga čiji je hitac bio smrtonosan. Na kraju su se Sem, Bil i Don složili da spor reše pištoljima u dvoboju pod sledećim neobičnim uslovima. Duelisti se nalaze u temenima jednakostraničnog trougla. Redosled pucanja određuje se žrebom.
Svako, kada na njega dođe red, ispaljuje jedan hitac pri čemu može birati u koga će da puca. Borba se prekida kada dvojica budu pogođena. Poredak pri gađanju, koji je određen žrebom pre početka duela, ne menja se u toku borbe.

Sva trojica znaju da Sem nikad ne promašuje, Bil pogađa u 80%, a Don u 50% slučajeva. Koji od duelista ima najviše šansi da ostane nepogođen, podrazumevajući da se svako pridržava sopstvene optimalne strategije? Naći kolika je verovatnoća za svakog duelistu da ostane nepogođen.
Ovaj problem verovatno asocira dobar broj čitalaca na nezaboravnu završnu scenu iz čuvenog vesterna The Good, the Bad and the Ugly, Serđa Leonea (1966) u kome Klint Istvud (Blondie), Li van Klif (Angel Eyes Angel) i Eli Valah (Tuco) raščišćavaju račune u troboju na groblju u međusobnom revolveraškom obračunu.
Verovali ili ne, najveću verovatnoću da ostane nepogođen u pomenutom troboju ima Don koji važi za najgoreg strelca! Za njim sledi Sem koji uvek pogađa. Kako Sem i Bil, kad na njih dođe red, gađaju jedan u drugog (da bi eliminisali boljeg strelca), optimalna strategija Dona sastoji se u tome da namerno promašuje („puca u vazduh”) kada na njega dođe red sve dotle dok jedan od njegovih protivnika ne bude pogođen. Posle toga on gađa u nepogođenog protivnika imajući, svakako, veće preimućstvo u odnosu na njega („prednost prvog poteza”).
Zadatak se rešava primenom osnovnih osobina i teorema iz teorije verovatnoće koje najverovatnije nisu poznate širokom krugu čitalaca. Zbog toga dajemo samo krajnje rezultate. Neka P(L) označava verovatnoću da lovac L jedini ostane nepogođen, tada je:
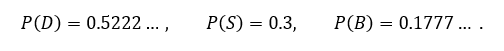
Prema tome, najveće šanse da u troboju ostane nepogođen ima najgori strelac Don (oko 52%), zatim Sem (30%) i na kraju Bil (oko 18%). Kompletno rešenje može se naći u knjizi autora ovog članka „Zašto je matematika lepa”? (2015) u izdanju autora i Udruženja književnika „Branko Miljković”, Niš.
Kada su jednog poznatog matematičara pitali da li je iznenađen paradoksalnim rešenjem problema troboja, odgovorio je: „Ne znam šta da mislim, ali kad dobro razmislim, mislim da nije ispalo onako kako sam mislio”.









Gavrilova truba je dobila taj naziv po tome što će arhanđel Gavrilo sa svojom trubom najaviti drugi dolazak Isusa Hrista na Zemlju, Sudnji dan, kada će se na jednom mestu sresti naše konačno vreme (konačna zapremina trube) i večnost budućeg veka (beskonačna površina trube).
Objašnjenja racionalnog nema. Objašnjenja tipa da ne možemo napraviti beskonačno veliku Toričelijevu trubu ništa ne znači. Ionako se bezbrojni matematički dokazi ne verifikuju tako štao se prave neki predmeti. Ista pogrešna logika je i u ni „čestice” boje ne mogu da budu manje od molekula. Zar moramo bojiti loptu da bi potvrdili da je njena površina 4 π r^2, gledajući koliko je boje ostalo u kanti? Na srpskoj Vikipediji su takođe neuspeli pokušaji objašnjenja paradoksa. Kao nema dovoljno boje da se oboji i spolja!? A imali je beskonačno mnogo da se oboji spolja. Ko je to pisao ne zna da bekonačno puta 2, ili podeljeno 2, ili sa 200 zilijardi, opet beskonačno.
Umesto: A imali je beskonačno mnogo da se oboji spolja.
Treba: A imali smo je beskonačno mnogo da se oboji iznutra.