Amerikanac mađarskog porekla rođen kao Janoš Lajoš, smatra se jednim od najvećih naučnika 20. veka. Još kao dete u rodnoj Budimpešti ispoljio je izuzetne sposobnosti i neverovatnu memoriju. U ovom prilogu prikazano je nekoliko zanimljivih detalja iz njegovog burnog života, od nauke do anegdota i rekreativnih matematičkih zadataka.

Prof. dr Miodrag Petković
Džon fon Nojman (John von Neumann) je rođen 28. decembra 1903. u Budimpešti (Mađarska) a umro je 8. februara 1957. Smatra se jednim od najvećih matematičara 20. veka. Fon Nojman je započeo svoj naučni rad u Budimpešti, Berlinu i Hamburgu, a zatim je od 1930. nastavio karijeru u SAD. Dao je značajne doprinose u teoriji skupova, kvantnoj fizici, funkcionalnoj analizi, teoriji operatora, logici, meteorologiji, verovatnoći, kompjuterskim naukama i dr. Postavio je osnove matematičke teorije igara i primenio ih u ekonomiji. Fon Nojman je učestvovao u razvojnom procesu računara i projektu „Menhetn” (za vreme Drugog svetskog rata), čiji je cilj bio konstrukcija prve atomske bombe.
Džon fon Nojman (AMS)
Džon fon Nojman je još kao dete demonstrirao neverovatnu memoriju. Postoje mnoge priče o tome. Sa šest godina bio je u stanju da razmenjuje šale sa svojim ocem na klasičnom grčkom i da deli osmocifrene brojeve napamet. Porodica Nojman je ponekad zabavljala goste prikazujući Džonovu sposobnost da memoriše telefonski imenik. Gost bi izabrao nasumice stranicu i kolonu telefonskog imenika. Mladi Džoni (na mađarskom Janoš Lajoš) bi zatim pročitao izabranu kolonu nekoliko puta, a onda bi odgovarao na bilo koje postavljeno pitanje u vezi s tim: ko ima taj-i-taj broj ili da izrecituje imena, adrese i brojeve po redu. Sa osam godina savladao je osnove diferencijalnog i integralnog računa. Takođe je voleo istoriju i kako je pamtio sve što pročita, postao je znalac u mnogim oblastima kao što su istorija Vizantije, detalji suđenja Jovanki Orleanki, Američki građanski rat itd.
Fon Nojman (ime koje je sam sebi dodelio, dok je Janoš angloameričko Džon) stigao je 1930. u Prinston (država Nju Džerzi, SAD) kao gostujući predavač Prinstonskog univerziteta. Istovremeno je istraživao i u Institutu za napredne studije, koji se takođe nalazi u Prinstonu i na kome su, u različitim vremenskim razdobljima, radili čuveni naučnici Albert Ajnštajn, Kurt Gedel, Robert Openhajmer, Volfang Pauli, Pol Dirak, Andre Vej i mnogi drugi. Osim u naučnom radu, fon Nojman je uživao u različitim neformalnim aktivnostima živeći načinom života koji se veoma razlikovao od stila konvencionalnog profesora.
Nojmanova predavanja nisu bila jednostavna za praćenje. Bujicu njegovih misli bilo je teško slediti, naročito onima manje talentovanim. Bio je „ozloglašen” zbog pisanja jednačina na minijaturnim slobodnim delovima table i njihovog brisanja pre nego što bi studenti uspeli da ih zapišu. Nojman je, takođe, često koristio sunđer za prepravljanje formula da bi na taj način uštedeo vreme. Ispisao bi na tabli formulu o kojoj se diskutuje, a zatim, ne prestajući da priča, samo bi načinio izmene u njoj ne prepisujući je celu nego samo brišući određeni simbol i pišući novi na njegovom mestu. Za Nojmana je matematika bila poput lake igre i zabave. Jednom prilikom je izjavio: „Ako ljudi ne veruju da je matematika jednostavna, to je samo zato što ne shvataju koliko je život komplikovan”.
Interesantno je pomenuti da je Džon fon Nojman pored doktorata iz matematike imao i diplomu hemičara. Ta univerzalnost bila je od velike koristi pri dizajniranju i konstrukciji prve atomske bombe (projekat „Menhetn”). Nojman je bio taj koji je proračunao (što je i usvojeno) da je atomska bomba efikasnija ako eksplodira nekoliko kilometara iznad mete nego na tlu. Od njega potiče i kovanica „kiloton”.
Fon Nojman je bio i mozak i inspiracija pri dizajniranju i konstrukcijii prinstonskog računara – jednog od prvih programabilnih računara poznatog pod jednostavnim nazivom IAS kompjuter (IAS je skraćenica za Institute for Advanced Stydy). To je bilo doba kad su velike računske mašine bile poznate pod imenima kao što su MANIAC, EDVAK, ENIAC, ILLIAC i slično. Kažimo uzgred da je prethodno radio na projektima EDVAK i ENIAC– ništa nije moglo bez Džona fon Nojmana u tehničkom progresu SAD, bile su reči američkog predsednika Dvajta Ajzenhauera kada mu je dodeljivao Medalju slobode.

Sl. 2 IAS računar, Nacionalni muzej američke istorije
(Vašington), (Wikipedia)
Priča se da je Nojman znao sve elektronske komponente IAS računara i da je nadzirao njegovo sklapanje. Kad je mašina bila skoro sasvim gotova, on je zbijao šale o njemu na sopstveni račun. Govorio je, „Ne znam koliko će zaista biti od koristi, ali u najmanju ruku, dobićemo puno pohvala na Tibetu za kodiranje Om Mani Padme Hum (tibetanska molitva) sto miliona puta na sat. On će nadaleko nadmašiti sve ono što molitveni cilindri mogu da postignu.” (Om Mani Padme Hum, u prevodu O, ti cvete lotosa – tekstovi tibetanskih budističkih molitvi su obično „narolani” na specijalne cilindre koji se ručno okreću za vreme molitve, sl. 3). Pre svečanog puštanja u rad IAS računara, fon Nojman je izjavio „Dobra vest je da će računar verovatno da funkcioniše na zadovoljavajući način. Loša vest je da je dobra vest malo verovatna.”

Sl. 3 Tibetanski molitveni cilindri (Wikipedia)
Fon Nojman i njegova (druga) supruga Klara vodili su veoma nekonvencionalan život. Zabave i noćni život bili su sastavni deo toga. Dok je radio u Nemačkoj bio je stalni posetilac berlinskih kabarea i drugih vidova noćnog života, a slično je nastavio i u SAD. Fon Nojman je živeo punim životom ali njegova smrt je bila tragična. Umro je od raka kostiju i pankreasa, verovatno nastalog kao posledica zračenja prilikom eksperimenata u Nju Meksiku na razvoju atomske bombe (projekat „Menhetn”). Panično je odbijao do poslednjeg dana pomisao da će prestati da postoji i da će njegov um prestati da funkcioniše.
O fon Nojmanu postoje brojne anegdote, od kojih je neke opisao njegov blizak prijatelj istaknuti matematičar mađarskog porekla Pol Halmoš u svom radu The legend of John von Neumann (The American Mathematical Monthly, 80 (1973). Jedna govori o putovanju vozom. Nojman je tokom puta ogladneo pa je zamolio konduktera da mu pošalje čoveka koji prodaje sendviče. Mrzovoljni kondukter je odgovorio „U redu, ako ga budem video”. Na to je Nojman odgovorio: „Pa trebalo bi. Ovaj voz je linearan, zar ne?” Drugom prilikom je kupovao kartu na blagajni železničke stanice i zamolio da bude povratna. „Dokle?”, pitao je blagajnik. „Pa dovde, naravno!”, odgovorio je Fon Nojman.
Druga anegdota govori o Nojmanovoj strasti za vožnjom automobilom, mada je bio loš vozač. U Prinstonu je čak postojalo „fon Nojmanovo ćoše”, gde je on napravio više udesa u stanju dokone nemarnosti. Jednu od svojih lomljava kolima, ovako je objasnio: „Ja sam lepo vozio putem brzinom od 60 milja na sat dok su stabla drveća sa moje desne strane prolazila pored mene ravnomerno tom istom brzinom. Odjednom mi je jedno drvo preprečilo put i bum!” Ovi bumovi bili su tako česti da je jedino efikasno antibum sredstvo bilo suprugino insistiranje da mu, s vremena na vreme, zabrani da vozi.
Džon fon Nojman je jednom prisustvovao predavanju iz fizike. Predavač je prikazao slajd s mnogo eksperimentalnih podataka i mada im je distribucija bila loša, on je tvrdio da većina leži na jednoj krivoj. Priča se da je Nojman promrmljao, „Pa bar leže u istoj ravni”.
U vezi s Nojmanovom neverovatnom memorijom i sposobnošću da izvodi komplikovane matematičke operacije napamet, u knjigama rekreativne matematike se sreće sledeći problem: „Devojka je udaljena 500 metara od zida a na njenoj glavi odmara se ptica. U jednom momentu i devojka i ptica počinju da se kreću pravolinijski prema zidu. Devojka ide brzinom od jednog metra u sekundi, a ptica leti brzinom od tri metra u sekundi. Kada ptica dođe do zida, ona odmah menja smer i vraća se pravo do glave devojke, menja smer i leti prema zidu. Ovaj od-glave-do zida i od-zida-do-glave ptičji let se neprekidno odvija sve dok devojka ne dođe do zida. Odrediti ukupnu dužinu puta koji je preletela ptica, smatrajući da pri zaokretima ne dolazi do gubitka brzine ptice (sl. 4).”
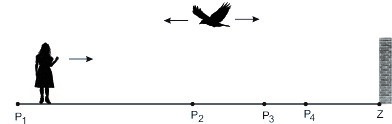
Sl. 4 Devojka i ptica
Mnogi amateri, ali i stručnjaci pokušavaju da reše ovaj problem birajući težak put. Oni sumiraju dužine ptičje putanje od devojke do zida i od zida do devojke. Ove dužine postaju sve kraće i kraće, i ovakav prilaz vodi do sumiranja beskonačnog reda, što je relativno komplikovano. Međutim, do rešenja se može doći na vrlo jednostavan način, čak bi se moglo nazvati trikom. Dovoljno je primetiti da je devojci potrebno 500 sekundi da bi došla do zida. Sve ovo vreme ptica leti i za 500 sekundi prelazi: (3 metra/sek) x (500 sekundi)=1.500 metara.
Kada se zna put ka rešenju onda je sve vrlo jednostavno, ali je po jednoj analizi otprilike polovina testiranih univerzitetskih profesora odmah krenula da traži rešenje upravo sumiranjem reda.
Legenda kaže da, kada je na jednom prijemu neki srednjoškolski profesor postavio Džonu fon Nojmanu ovaj zadatak, on je malo razmislio i brzo saopštio rešenje. Profesor je rekao „Ah, vi ste uočili trik”.Nojman, koji je bio poznat po brzini računanja napamet, odgovorio je: „Kakav trik? To je bio jedan jednostavan red.”
Ovo sumiranje zahteva čitavu stranicu punu matematičkih relacija te je iz tog razloga izostavljeno da ne bismo zamarali čitaoce. Uporni mogu da pokušaju ono što je fon Nojman uradio napamet za nekoliko sekundi.
Putovanje devojke i ptice može se pregledno predstaviti pomoću grafika prostor-vreme, sl. 5. Strmine prikazanih duži su proporcionalne brzinama Vd i Vp devojke i ptice. Tačke P1, P2, P3…označavajutačke kontakta devojke i ptice. Naravno, mi ne možemo da završimo putanju ptice do zida Z jer cik-cak putanje postaju beskonačno male.
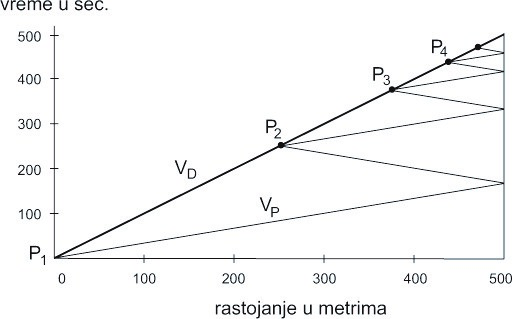
Sl. 5 Prostor-vreme grafik problema devojke i ptice
Čitaocima se preporučuje sledeći zadatak istog tipa kao gore opisani, naizgled vrlo komplikovan, ali prava ideja ga svodi na zadatak iz fizike za osnovne škole.
Dva automobila, koja u isto vreme polaze iz mesta A i B međusobno udaljenih 420 km, kreću se jedan prema drugom sve do njihovog susreta u tački C. Njihove brzine su 80 i 60 km na sat. Tačno u vreme njihovog starta poleće ptica iz A brzinom od 100 km na sat i kreće se pravo prema drugom automobilu koji je pošao iz B. Kada stigne do njega, ptica se odmah okreće i leti nazad prema automobilu koji se kreće prema B. Posle susreta sa ovim automobilom ptica se okreće i leti u suprotnom smeru itd. Sve vreme dok se automobili kreću jedan prema drugom ptica leti od jednog do drugog brzinom od 100 km na sat. Koliki put je preletela od momenta polaska do momenta susreta dva automobila?
Postoje nesuglasice u vezi sa ovim problemom: prethodno je opisan zadatak o devojci i ptici (priča potiče od Nojmanovog prijatelja već pomenutog Pola Halmoša), dok prema Borvejnu i Bejliju (Mathematics by Experiment, A K Peters, 2003) fon Nojman je napamet sumirao red koji proizilazi iz zadatka o dva automobila. U filmu Beautiful Mind, režisera Rona Hauarda iz 2001, Džon Neš (koga glumi Rasel Krou) diskutuje o ovom problemu s kolegama u univerzitetskoj bibliotreci.
Interesantna simulacija varijante automobile-i-ptica problema može se naći na linku https://mathworld.wolfram.com/TwoTrainsPuzzle.html








