Jedan od najslavnijih ljudi svog doba svakako je bio italijanski naučnik Đirolamo Kardano (1501–1576). Bio je univerzalist, radio je kao matematičar, fizičar, lekar, astronom, astrolog i profesor na univerzitetima u Paviji, Milanu i Bolonji. Međutim, zbog svog više nego nezgodnog karaktera, sklon kockanju, svađama i podvalama, više puta hapšen, i danas važi za jednog od najkontroverznijih naučnika u istoriji.

Prof. dr Miodrag Petković
Đirolamo Kardano (1501-1576) bio je jedan od najslavnijih ljudi svog doba i majstor mnogih veština; radio je kao matematičar, fizičar, astronom, lekar, astrolog i profesor na univerzitetima u Paviji, Milanu i Bolonji. Istovremeno, on je jedna od najkontroverznijih osoba u istoriji nauke.


Sl. 1 Ars Magna,Đirolamo Kardano (Wikipedia)
Kardanovo najznačajnije matematičko delo Ars Magna (Velika veština, štampano u Nirnbergu 1545), jedna od najuticajnijih knjiga iz oblasti matematike u 16. veku, sadrži formulu za rešavanje kubne jednačine, poznatu danas kao Kardanova formula. Kubna jednačina se najčešće posmatra u obliku
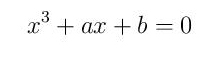
jer se opštiji oblik
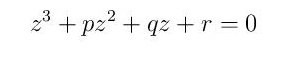
smenom
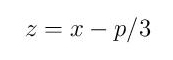
svodi na razmatrani oblik
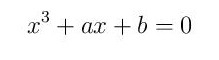
Tada su rešenja ove kubne jednačine data formulom
(1)
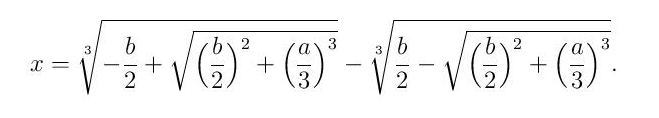
S obzirom da treći koren ima tri vrednosti (grane), postoji 9 kombinacija tako da izbor tri prave grane predstavlja dodatni problem. Ovu formulu je Kardano saznao od drugog velikog italijanskog matematičara tog doba Nikole Tartalje (pravo ime Nikolo Fontana, tartalja – mucavac) je nadimak), tako da je zbog objavljivanja Tartaljinog rezultata bez njegove saglasnosti u Kardanovoj knjizi došlo do oštrog i mučnog spora između ove dvojice naučnika. Danas je poznato da je do rešenja u opštem obliku prvi došao Scipion del Fero (1465-1526), nekoliko godina pre Tartalje. Bez obzira na ove činjenice formula (1) je naširoko poznata kao Kardanova formula (jedna od njegovih većih prevara) jer ju je on prvi opisao u svojoj knjizi Ars Magna (1545).
Opisani primer „pozajmice” tuđeg rezultata samo govori o tome koliko je Kardano bio kontroverzna osoba. Njegov buran život bio je ispunjen uspesima i tragedijama, usponima i padovima, što ga čini jednim od najneobičnijih karaktera u istoriji matematike i nauke uopšte jer je on bio „majstor svih zanata”. On je bio čovek neočekivanih kontrasta. Uprkos tome što se nije mogao pohvaliti „ni stasom ni glasom” zbog niza fizičkih mana, bio je veoma samouverena osoba koja je na svakom mestu, od kafana do kraljevskih dvorova, nastupala s pozom „zar nisam najpamentniji”.
Šah i kocka su mu bile velike strasti, pri kockanju je prvi put u istoriji koristio neke elemente verovatnoće, matematičke oblasti koju su nešto kasnije zasnovali Ferma i Paskal. Iz kockarskih burnih svađa zadobio je brojne ožiljke, a u jednoj prilici optužen je za ubistvo. Takođe je ostalo nerazjašnjeno trovanje njegovog studenta Ludovika Ferarija koji je izveo formulu za polinomsku jednačinu četvrtog stepena koristeći Feroov-Tartaljev-Kardanov metod.

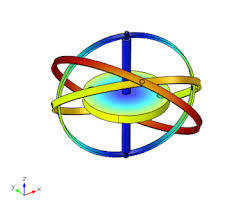
Sl. 2 Kardanov zglob (spojnica) i žiroskop (comsol.com)
Osim što je predavao medicinu i matematiku, Kardano je pisao radove iz aritmetike, astronomije, fizike, mehanike, hidrodinamike, geologije, i drugih oblasti. Njegovo glavno delo Ars Magna (1545) je prva velika studija na latinskom jeziku posvećena isključivo algebra, gde se prvi put pominju negativni brojevi. Verovatno su mnogi čitaoci čuli za kardanov zglob koji se koristi kod automobila i drugih mašina za transmisiju (rotacione) pogonske sile, ali je verovatno da vrlo mali broj ljudi zna da je to izum Đirolama Kardana. Osim toga, konstruisao je mehanizam koji se sastojao od tri koncentrična prstena koji slobodno rotiraju oko ose, što je predstavljalo preteču žiroskopa.
Na vrhuncu slave Đirolamo Kardano važio je za vodećeg svetskog naučnika svog vremena. Prema čuvenom istoričaru matematike E. T. Belu, on je više puta odbijen da bude imenovan za profesora na univerzitetu u Milanu, da bi se naposletku vratio kao rektor! Bio je, takođe, čuveni lekar (posao kojim se bavio ilegalno), čija je dobra reputacija daleko prevazišla ovaj grad jer je bio poznat u celoj Evropi. Godine 1552. prihvatio je poziv da pomogne Džonu Hamiltonu, škotskom nadbiskupu, koji je patio od teških napada astme. Vrlo brzo je zaključio da su ovi napadi uzrokovani jakom alergijom na perje, pa je zahtevao da se nadbiskupov jastuk zameni. Nakon uklanjanja izvora, nadbiskupovo zdravlje se momentalno poboljšalo, a Kardano je istovremeno postao i veoma slavan i veoma bogat.
Bio je manje uspešan kada se prihvatio da sačini horoskop mladog šesnaestogodišnjeg kralja Engleske, Edvarda Šestog (sina kralja Henrika Osmog i Džejn Sejmor, opisan na posredan način u knjizi Kraljević i prosjak Marka Tvena). Predvideo mu je dug i srećan život ali je, nažalost, kralj umro pre nego što se Kardano vratio kući iz Engleske.
Godine 1570. godine dospeo je u tamnicu u kojoj je proveo neko vreme. Uhapšen je jer je njegova ekstravagantna ideja da napravi horoskop Isusa Hrista protumačena od strane crkve kao jeres. Napustivši katedru na Univerzitetu u Bolonji, prešao je u Rim gde je postao istakniti astrolog i dobijao penziju od pape. Umro je u Rimu 1576. godine pod nerazjašnjenim okolnostima, što i nije bilo baš neobično jer je zbog svog nezgodnog karaktera imao veliki broj neprijatelja, od uličnih razbojnika i kockara, do samog pape.
Kratka priča dovoljno govori da je Đirolamo Kardano bio univerzalan naučnik nemirnog duha. Zato nije nikakvo čudo što se bavio i igračkama čije rešenje ima matematički karakter. Jedna od najpoznatijih je veoma rasprostranjena igračka, poznata kao kineski prstenovi na slici 3. Francuzi zovu ovu igračku La Baguenodier (igračka s kolutovima), a Englezi je zovu The Tiring Irons (umarajući okovi). Mada vrlo starog porekla, ona se i danas prodaje širom sveta. Uprkos svome imena, njeno navodno kinesko poreklo nije dokazano do današnjih dana; Đirolamo Kardano je bio prvi koji je opisao ovu igračku-zagonetku 1550. godine u delu De Subtilitate. Kasnije se ova zagonetka usput pominje u 7. glavi romana Hongloumeng (San crvene dvorane) iz 1791. Takođe ju je razmatrao engleski matematičar i sveštenik Džon Volis (1616-1703) u svojoj Algebri (izdanje na latinskom, 1693).
Igračka-zagonetka kineski prstenovi sastoji se od izvesnog broja prstenova okačenih na dugu žičanu petlju na takav način da je ona obuhvaćena prstenovima u početnom položaju (slika 3). Svaki prsten je labavo povezan pomoću malog vertikalnog držača za platformu ispod petlje. Osim poslednjeg (najudaljenijeg od kraja petlje), svaki od veznih držača je obuhvaćen odgovarajućim prstenom da bi se sprečilo izvlačenje prstena iz petlje. Prsten može da klizi duž petlje do njenog kraja i može se skinuti s petlje jedino ako su svi prstenovi od posmatranog prstena do kraja petlje već skinuti. Stavljanje na petlju odvija se obratnim redom. Poredak prstenova se ne sme menjati. Zadatak se sastoji u skidanju svih prstenova sa petlje u minimalnom broju poteza.
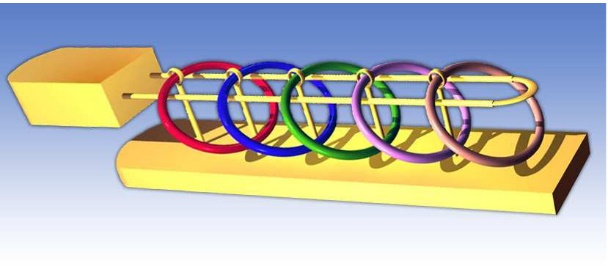
Sl. 3 Kineski prstenovi (Vladimir Petković)

Sl. 4 Hanojska kula (Vladimir Petković)
Slično kao u slučaju dobro poznate hanojske kule (slika 4), pri rešavanju zagonetke kineski prstenovi neophodna je primena inverznog postupka (vraćanje prstenova natrag na petlju). Ova rekurzivna osobina tesno povezuje pomenute dve zagonetke. Štaviše, izvanredno lepe ideje (u oba slučaja zasnovane na korišćenju binarnog brojnog sistema) pri rešavanju čine ih veoma sličnim. Zagonetki kineski prstenovi posvećena je obimna literatura koja se sastoji od nekoliko knjiga i stotinak naučnih radova.Postupak za nalaženje ukupnog (minimalnog) broja koraka, neophodnih za izvlačenje svih n prstenova sa petlje, opisali su Rauz Bol i Kokseter u knjizi Mathematical Recreations and Essays (Dover Publication, Njujork 1987). Minimalni broj poteza je
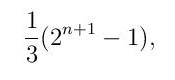
ako je n neparno i
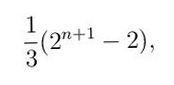
ako je n parno.
Napomenimo da Đirolamo Kardano i Džon Volis nisu našli optimalan postupak za rešavanje zagonetke s prstenovima (samim tim, nisu ni znali minimalan broj poteza). Elegantno rešenje dao je francuski matematičar Luj Gro (Louis Gros) u studiji Thèorie du Baguenodier (Lion, 1872). Njegov pristup rešavanju se može smatrati pretečom tzv. Grejovih kodova, nazvanih tako po inženjeru Frenku Greju (Frank Gray), zaposlenom u kompaniji AT&T Bell Laboratories, koji je radio na razvoju tehnike (de)kodiranja i korekcije greške tridesetih godina dvadesetog veka. Podsetimo da je francuski inženjer Emil Bodo koristio ovu vrstu kodova u telegrafiji 1878. godine, znatno pre Greja.
Frenk Grej je izumeo metod za konverziju analognog signala u binarni Grejov kod koristeći vakuumske cevi. Danas Grejovi kodovi imaju značajnu primenu u teoriji grafova i teoriji brojeva, a koriste se i u korekciji grešaka u digitalnim komunikacijama, kao što je transmisija TV signala, i da učine transmisiju sistema manje osetljivom na šumove. Njihovo generisanje dato je u tabeli 1.
U tabeli 1 prikazani su decimalni brojevi od 0 do 21 u binarnoj reprezentaciji (sa osnovom 2). Ovim binarnim brojevima generisani su Grej-kod binarni brojevi. Svaki petocifreni Grej-kod broj se dobija iz odgovarajućeg binarnog broja na osnovu sledećeg pravila: računajući binarne brojeve sleva na desno, prva Grej-kod cifra je uvek jednaka prvoj cifri binarnog broja. Posle toga, svaka Grej-kod cifra je 1 ako se odgovarajuća binarna cifra razlikuje od svoje prethodne (posmatrajući ulevo); u suprotnom, ova cifra je 0.
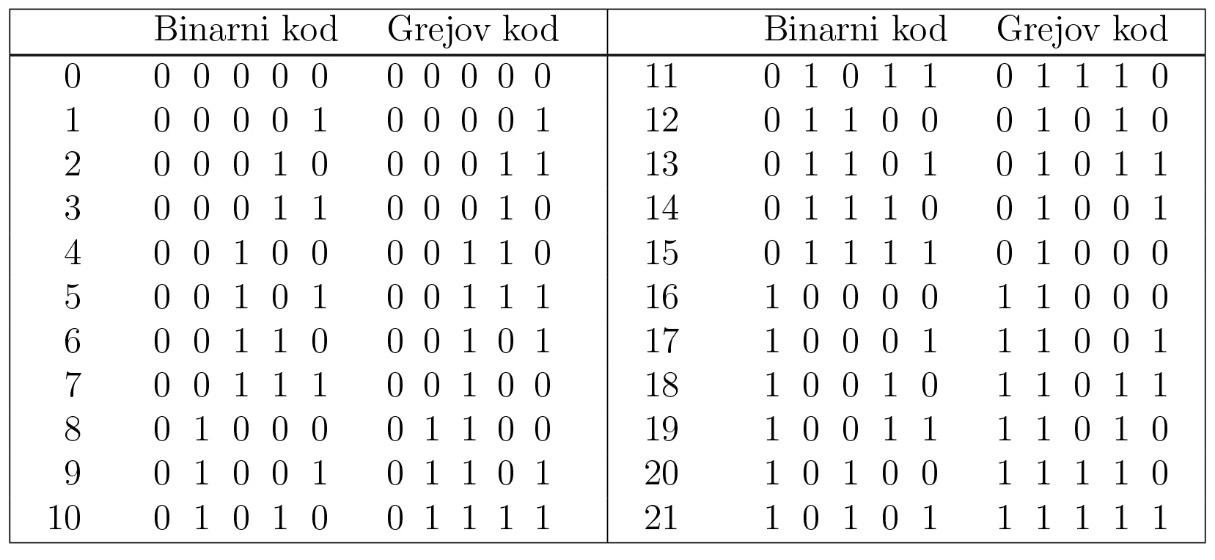
Tabela 1 Binarni brojevi i Grej-kod brojevi
U nastavku ćemo izložiti deo procesa za rešavanje zagonetke sa 5 prstenova zasnovano na binarnim i Grej-kod brojevima. Na osnovu prethodnog, sledi da optimalno rešenje zahteva (2^6-1)/3=21 potez. Svaka pozicija prstena se predstavlja pomoću Grejovog petocifrenog binarnog niza nula i jedinica, pri čemu prstenu na petlji odgovara 1, a prstenu van petlje 0. Poslednja cifra odgovara poziciji prvog prstena (najbližeg kraju petlje), dok prva cifra odgovara poziciji petog prstena. Ilustracije radi, dajemo nekoliko pozicija prstenova i odgovarajuće Grejove (petocifrene) binarne brojeve:
1 1 1 1 1 (svi prstenovi su na petlji),
1 0 1 1 1 (četvrti prsten je van petlje),
1 1 0 1 0 (prvi i treći prsten su skinuti),
0 0 0 1 1 (prvi i drugi prsten su na petlji),
0 0 0 0 0 (svi prstenovi su skinuti).
Na veliko iznenađenje, postoji neverovatna koincidencija između Grej-kod binarnih brojeva i rešenja zagonetke s prstenovima: u obratnom redosledu (od 21 do 0 u slučaju pet prstenova) Grej-kod brojevi upravo pokazuju sukcesivne pozicije prstenova u traženom minimalnom rešenju, pri čemu prvi Grej-kod broj 11111 pokazuje početni položaj (svi prstenovi su na petlji). Na osnovu tabele 1 možemo napraviti šemu (prikazanu na slici 5) koja slikovito prikazuje prve poteze potrebne da bi se skinula tri prstena sa petlje. Pridruženi Grej-kod brojevi prikazuju sukcesivne pozicije prstenova, predstavljenih malim kružićima.
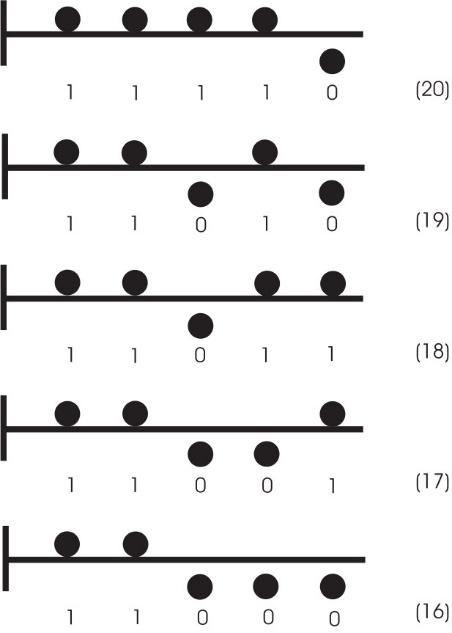
Sl. 5 Pet prstenova i odgovarajući Grej-kod brojevi








