Iako je bio jedan od najvećih svetskih autora matematičkih i logičkih zagonetki, rebusa, šahovskih problema i zanimljivih igračaka (zvali su ga „Kralj zagonetki”), imao je popriličnu manu – prisvajao je zagonetke drugih autora i objavljivao ih pod svojim imenom, što mu je najčešće i uspevalo jer je bio prvoklasan manipulator i menadžer.

Prof. dr Miodrag Petković
Povremeno će se u ovoj rubrici u pojavljivati zanimljivi prilozi iz sveta matematike koji uključuju interesantne matematičke formule, događaje iz sveta matematike i života velikih matematičara, kao i elementarne ali intrigantne i izazovne zadatke za čije rešavanje je dovoljno srednjoškolsko znanje matematike. Većina ovih priloga, kao i još matematičkih priča i zanimljivosti može se naći na sajtu autora ovih priloga, opcija teme:
Krajem 19. veka Lojdova „slagalica-15”, Amerikanca Semjuela Lojda (1841-1911), izazvala je pravu svetsku histeriju. Slagalica ima 15 kvadratnih pločica i jedno prazno mesto na ploči dimenzije 4×4. Ove pločice su smeštene u kutiji tako da se ne mogu vaditi, ali se mogu pomerati horizontalno i vertikalno. Na početku, pločice su poređane kao na slici 1, redom od 1 do 13, zatim 15 pa 14.
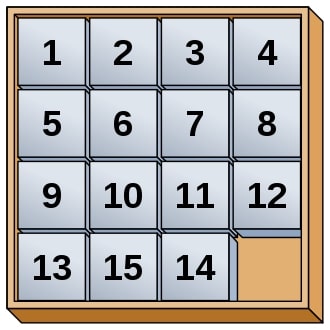
Sl. 1 Lojdova slagalica s 15 brojeva
Treba reći da Semjuel (Sem) Lojd nije kreator slagalice već Nojes Čepman koji je lansirao ovu zagonetku 1880. Godine 1891. Sem Lojd je objavio slagalicu pod svojim imenom i tako je ostalo i do danas. Iako je bio jedan od najvećih svetskih autora matematičkih i logičkih zagonetki, rebusa, šahovskih problema i zanimljivih igračaka (zvali su ga „Kralj zagonetki”), imao je popriličnu manu – prisvajao je zagonetke drugih autora i objavljivao ih pod svojim imenom, što mu je najčešće i uspevalo jer je bio prvoklasan manipulator i menadžer.
Kod slagalice-15 zadatak se sastoji u tome da se kvadratne pločice pomeraju gore, dole, desno i levo, koristeći prazan kvadrat, sve dok se brojevi ne postave u strogo rastućem poretku 1, 2…14, 15. Priča se da je Sem Lojd ponudio 1.000 dolara za tačno rešenje (danas bi to bilo oko 30.000 dolara). Odmah da kažemo da je Lojd, kao dobar matematičar, znao da iz ove početne pozicije zagonetka nema rešenje tako da je i mogao da bude tako darežljiv.
Interesantna je priča o Lojdovom pokušaju da patentira ovu slagalicu.
Kada ga je službenik patentnog ureda zamolio da demonstrira rešenje, Lojd je odgovorio da to nije moguće (naravno, reč je o početnoj poziciji 15-14 koja se nalazila u kutijama). „Naš zavod prihvata patente samo onih stvari koje rade, ovde to nije slučaj”, odgovorio je službenik i odbio zahtev. Slagalica se i dan-danas može nabaviti u radnjama sa igračkama i to u raznim varijantama (često i kao slagalica-mozaik umesto brojeva).
Čitaoce sigurno zanima pod kojim uslovima je moguće rešiti Lojdovu slagalicu. Postoje početne pozicije za koje je moguće rešiti slagalicu, dok za druge početne pozicije to nije moguće, i to u odnosu otprilike pola-pola. Ova činjenica je veoma impresionirala matematičare tokom decenija, i oni su se dali na posao da matematičkim putem odrede kada je slagalicu moguće rešiti, a kada ne.
Pre nego što damo uslove pod kojima je moguće rešiti slagalicu-15, podsetimo se nekih najosnovnijih osobina iz oblasti matematike koja se naziva kombinatorika. Posmatrajmo skup S={a,b,c}od 3 elementa. Tada se pod permutacijom bez ponavljanja reda 3 podrazumevaju svi rasporedi (1,2,3), (1,3,2), (2,1,3), (2,3,1), (3,1,2), (3,2,1). Dužina permutacije može biti i manja od ukupnog broja elemenata skupa S, na primer, ako je dužina 2 tada imamo sledeće permutacije reda 2: (1,2), (2,1), (1,3), (3,1), (2,3), (3,2).
Važan pojam u kombinatorici jeste inverzija permutacije: uređen par elementa {Pi,Pj} (kod koga se zna koji element je na prvoj, a koji na drugoj poziciji) naziva se inverzijom u permutaciji P ako se Pijavlja pre Pi, a pritom je Pi > Pj.Na primer, permutacija (3,1,4,5,2) ima 4 inverzije (3,1), (3,2), (4,2) i (5,2).
Ukupan broj inverzija I(P)u permutaciji P dobija se kao suma elemenata vektora permutacionih inverzija. Broj inverzija u permutaciji je jednak broju razmena susednih elemenata neophodnih za dobijanje njihovog prirodnog uređenja. Primetimo da u pravougaonoj slagalici bilo koje dimenzije m x n koja ima jedan prazan kvadrat, svako pomeranje jedne pločice menja broj inverzija u permutaciji za dva; paran broj ostaje paran a neparan ostaje neparan.
U slučaju Lojdove slagalice-15 {P1,P2…P15} neka je i redni broj kvadata slagalice računajući počev od prvog elementa prve vrste i idući s leva na desno, vrstu po vrstu. Ako je broj Pi veći od Nibrojeva koji se javljaju posle broja Pi, kažemo da je red njegove inverzije jednak Ni. Ukupan broj inverzija jednak je
I(P) = N1 + N2 +… + N15 = N2 +… + N15,
pri čemu se sabiranje može vršiti od 2 do 15 jer je uvek N1 = 0s obyirom da ne postoje prirodni brojevi manji od 1.
Za one koji nisu dovoljno upoznati sa terminom permutacija, pojasnićemo gornje izlaganje na sledećem primeru početne pozicije u slagalici-15 predstavljene preko kvadratnih šema 4 x 4 broa, slika levo. Na slici desno je broj inverzija za odgovarajući broj iz šeme na levoj strani. Na primer, za broj 7 (levo) broj inverzija je 4 jer se 7 javlja ispred brojeva 4, 8, 1, 12, 14, 9, 3, 15, 2, ali je veći samo od 4, 1, 3 i 2.
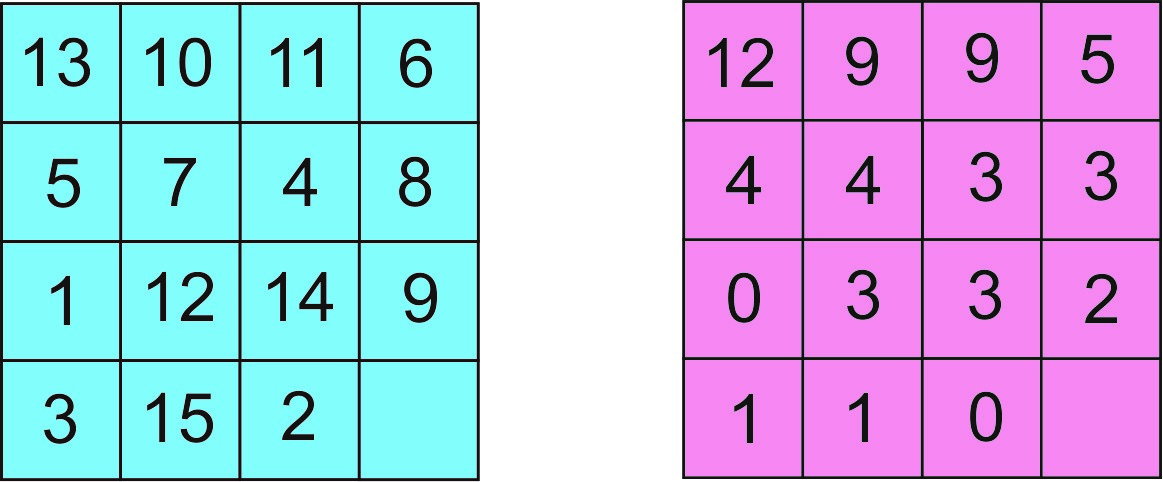
Iz šeme inverzija (desno) nalazimo da je ukupan broj inverzija I(P) = 59.
Matematičari su brzo došli do uslova za rešivost slagalice 15:
Ako je ukupan broj inverzija I(P) koji se odnosi na početnu poziciju paran, rešenje slagalice-15 postoji; ako je ovaj broj neparan, rešenje ne postoji.
Na osnovu ovog uslova rešivosti sledi da je poslednji primer slagalice nerešiv jer je ukupan broj inverzija 59 neparan broj. U slučaju Lojdove zagonetke sa zamenjenim mestima brojevima 14 i 15 (slika 1) imamo da je N14 = 1, dok za sve ostale važi Ni = 0Prema tome, I(P) = 1dakle neparan broj, tako da se iz početne pozicije koju je zadao Lojd postavljanje brojeva u rastući niz od 1 do 15 ne može postići.
Nemački matematičar V. Arens opisao je atmosferu u Evropi nastalu posle pojave Lojdove slagalice:„Krajem devetnaestog veka slagalica ,petnaest’ pojavila se u SAD i vrlo brzo se proširila zahvaljujući ogromnom broju igrača koje je osvojila izazvavši velike nevolje. Ista stvar se desila i u Evropi. U kancelarijama i prodavnicama poslodavci su bili užasnuti ponašanjem zaposlenih koji su igrali igru za vreme radnog vremena i školskih časova. Čak su se i ozbiljni i vremešni poslanici za vreme zasedanja nemačkog Rajhstaga (parlamenta) zabavljali ovom slagalicom. Vlasnici radnji su zaboravljali da ujutru otvore svoje radnje, vozovi su kasnili, brodovi su udarali u dokove, uvažena gospoda su u kasnim večernjim satima ispod uličnih lampi rešavala slagalicu. Na ulicima su se prolaznici sudarali obuzeti premeštanjem pločica, igralo se po parkovima i tramvajima. (Da podsetimo, nešto slično se desilo i sto godina kasnije saRubikovom kockom i igrom ,tetris’). Iz Pariza igra se brzo proširila iz glavnog grada na sve provincije. Jedan francuski novinar je pisao da je skoro svaka seoska kuća u provinciji imala ovu slagalicu i čitava domaćinstva su zaboravljala (ili odlagala) poljoprivredne radove da bi rešavali Lojdovu slagalicu.”
Razlog za ovu histeriju je lako objasniti; igra je dovoljno jednostavna tako da je mogao da je igra svako, želja za uspehom bila je ogromna (u to vreme nudile su se i nagrade za uspešno rešenje), a histerija je predugo trajala jer slagalica sa početnom pozicijom nije mogla da se složi kako je zahtevano.
Interesantno je napomenuti da je čuveni šahista i bivši svetski prvak Bobi Fišer bio ekspert za rešavanje ove zagonetke-igračke; on je bio u stanju da reši slagalicu za manje od 30 sekundi iz bilo koje rešive početne pozicije.
Od interesa je pomenuti da Semjuela Lojda smatraju jednim od najvećih sastavljača matematičkih i logičkih zagonetki, šahovskih problema i rebusa. Ne samo amateri, već i univerzitetski profesori su dane i nedelje provodili u reševanju njegovih glavolomki. Zbog toga autor ovog priloga smatra da je on, osim slagalice, zaslužio da se pomenu još dve njegove čuvene zagonetke.
Prva od njih je matematičko-logičkog karaktera, opšte poznata pod imenom Anamarija problem, i glasi ovako:Ana i Marija imaju zajedno 44 godine. Marija je dva puta toliko stara koliko je Ana bila kada je Marija bila upola toliko stara koliko će Ana biti kada Ana bude tri puta toliko stara koliko je Marija bila kada je Marija bila tri puta toliko stara koliko je tada bila Ana.
Po koliko godina imaju Ana i Marija? Za rešavanje ovog problema dovoljno je znanje iz osnovne škole, naravno uz dobru ideju.
Rešenje: Neka je M broj Marijinih godina, a A Aninih. Dalje, neka je pre X godina „… Marija bila dva puta toliko stara koliko je Ana bila…”, a da će kroz Y godina „… koliko će Ana biti…”, i da je pre Z godina „… Marija bila tri puta toliko stara koliko je tada bila Ana”. Na osnovu ovog imamo sledeći sistem od pet jednačina:
M + A = 44
M = 2(A-X)
A + Y = 2(M-X)
A + Y = 3(M-Z)
M – Z = 3(A-Z).
Rešavanjem gornjeg sistema nalazimo da je M=27,5 i A=16,5. Dakle, Marija ima 27 i po, a Ana 16 i po godina.
Sem Lojd se smatra i jednim od najvećih sastavljača šahovskih problema svih vremena. Eksperti koji prate ovu posebno vrstu zadataka su saglasni da je on uneo u šahovsku kompoziciju skoro sve važne ideje, motive i teme, i to pre 150 godina. Za ljubitelje ove vrste zadataka, koji su decenijama (a i danas) bili sastavni deo skoro svih dnevnih novina i nedeljnika, evo jednog interesantnog šahovskog problema. Beli igra prvi i najdalje u svom trećeg potezu matira crnog. Rešenje izostavljamo da ne bismo kvarili užitak čitalaca pri rešavanju ovog čuvenog problema.
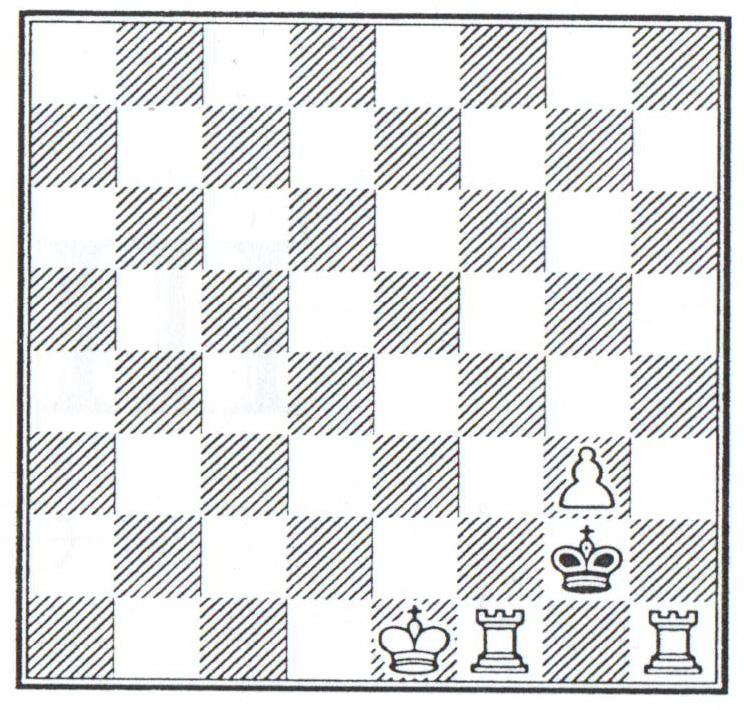









Putem imejla (dostupan preko mog sajta) nekoliko čitalaca zamolilo me za rešenje Lojdovog šahovskog problema – mat u 3 poteza. Evo rešenja:
Označimo vertikale šahovske table slovima a,b,c,d,e,f,g,h a horizontale brojevima od 1 do 8 (standardna šahovska notacija). U prvom potezu beli igra 1. Tf4. Ako crni kralj uzme topa na h1, beli igra kraljem 2. Kf2 i mat je neizbeżan topom na h4. Druga varijanta je mnogo interesantnija, zbog koje je problem i postao tako čuven. Ako crni kralj uzme pešaka na g3, beli vuče veoma domišljat potez: vrši malu rokada i crni će biti matiran u 3. potezu.
Postavlja se pitanje da li je Lojdova pozicija regularna? Naime, kako je crni kralj dosao na g2 s obzirom da beli kralj i ugaoni top na h1 nisu povukli nijedan potez (zbog kasnije rokade u resenju)?
Pitanje je sasvim na mestu, šahovski problem se smatra korektnim jedino ako je do postavljene pozicije moguće doći regularnim šahovskim potezima. Analiza korektnosti šahovskog problema pripada oblasti retrogradne analize, nekoj vrsti “šahovskog vremeplova.” Lojdov problem je korektan; jedna jednostavna pozicija iz koje se može doći je postavka u kojoj se crni kralj nalazi na polju h3, bilo koja crna figura na g3 i beli pešak na h2, dok su beli kralj i topovi na istim poljima kao na dijagramu. Beli uzima pešakom crnu figuru na g3 i topom daje šah a crni kralj dolazi na polje g2. I to je Lojdova pozicija data u prilogu. Alternativno, beli pešak može biti na polju f2, a crni kralj na f3.
I jedna ispravka tipo-greške u prilogu: umesto „… ako se Pi javlja pre Pi, a pritom je Pi > Pj“,
treba „…ako se Pi javlja pre Pj, a pritom je Pi > Pj“