Niko ne sumnja da je matematika neophodna za rešavanje problema u skoro svim granama nauke, istraživanja i razjašnjavanja raznih pojava u prirodi i društvu. U ovom prilogu ukazaćemo na dve interesantne primene matematike za rešavanje dva vrlo zanimljiva problema, od kojih jedan potiče još iz drevnog Egipta: da li zmija može da proguta samu sebe. Ni manje ni više, odgovor zahteva primenu više matematike – integralni račun.

Prof. dr Miodrag Petković
Problem 1: Crv na rastegljivom gumenom konopcu
Ovaj zadatak o crvu je postavljen u naučno-stručnom mesečniku Scientific American još pre 60 godina i izazvao veliko interesovanje čitalaca. Naravno, umesto crva može se posmatrati i bilo koji drugi živi stvor koji se ravnomerno kreće.
Crv se nalazi na jednom kraju gumenog konopca koji se (pretpostavimo) može beskonačno rastezati. Na početku konopac je dug 1 kilometar. Crv gamiže duž konopca prema drugom kraju konstantnom brzinom od 1 santimetra u sekundi. Na kraju svake sekunde konopac se trenutno rasteže za još jedan kilometar. Dakle, u prvoj sekundi crv prelazi 1 santimetar, a konopac postaje 2 kilometra dugačak. Posle druge sekunde crv je prešao još 1 santimetar, a konopac s produžio na 3 kiloemtra itd. Rastezanje konopca je ravnomerno, kao rastezanje gumene trake. U ovom procesu crv se pomera i to, kako zbog sopstvenog kretanja (1 cm/sec), tako i usled istezanja konopca. Može li pri opisanoj situaciji crv dosegnuti drugi kraj konopca? Ako je to moguće, odrediti približno vreme takvog putovanja i dužinu konopca na kraju putovanja.

Crv na rastegljivom gumenom konopcu
Pošto crv stalno napreduje, može se postaviti pitanje: Nije li očigledno da on mora konačno da stigne na cilj? Ne obavezno, jer može se večito konstantno napredovati ka cilju a da se nikad ne dođe do njega. Napredovanje crva meri se pomoću zbira (opadajućih) delova dužine konopca. Ovaj zbir može biti beskonačan, a da ipak konvergira ka tački koja je mnogo ispred kraja konopca. Zaista, takav slučaj bi se desio kad bi se konopac razvlačio udvostručavajući svoju dužinu nakon svake sekunde.
Međutim, pod uslovima u zadatku crv uspeva da stigne do kraja konopca, što izgleda neverovatno! Da vidimo da li matematika može da pruži objašnjenje za ovaj, na prvi pogled, neočekovan ishod?! Kako ima 100.000 santimetara u jednom kilometru, na kraju prve sekunde crv će prevaliti 1/100.000-ti deo dužine konopca. Tokom druge sekunde crv prevaljuje (počev od prethodne tačke nakon razvlačenja konopca) rastojanje od 1/200.000-tog dela dužine konopca koji se rastegao na dva kilometra. Tokom treće sekunde on prelazi 1/300.000-ti deo konopca (koji je sada dugačak tri kilometra), i tako dalje. Napredovanje crva, izraženo preko delova dužine celog konopca, iznosi
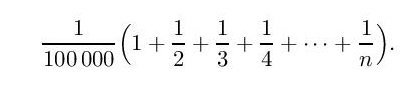
Zbir u zagradi je parcijalna suma dobro poznatog harmonijskog reda koji divergira kada n teži u beskonačnost. Čim parcijalna suma (izraz u zagradi) postane jednaka 100.000, gornji izraz će postati 1, što znači da je crv dostigao kraj konopca. Broj sabiraka n u ovoj parcijalnoj sumi harmonijskog reda biće jednak broju sekundi koje su istekle. Kako se crv kreće jedan santimetar u sekundi, n je takođe konačna dužina konopca u centimetrima.
Ovaj ogroman broj L, sa tačnošću u okviru jednog minuta, jeste
![]()
gde je e osnova prirodnog logaritma (približno 2.71828182) a
![]()
Ojlerova konstanta koja predstavlja graničnu konstantu niza
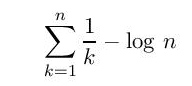
kada n teži u beskonačnost. Broj L dat gornjim izrazom daje dužinu konopca koja uveliko nadmašuje prečnik poznatog svemira i vreme koje prevazilazi sadašnje procene starosti svemira.
Iz rešenja ovog problema primetimo da će, nezavisno od parametara (početna dužina konopca, brzina crva i broj istezanja konopca), crv stići do drugog kraja konopca i to za konačno vreme. Naravno, pod pretpostavkom da se radi o zaista dugovečnom crvu. Isto bi važilo i ako se istezanje vrši kontinualno; međutim, zbog lakše analize, u postavljenom zadatku je pretpostavljeno da se istezanja konopca vrše u diskretnim koracima. Ovo je dobar primer koji može i univerzitetskom profesoru zadati mnogo glavobolje.
Primer 2: Samoproždiruća zmija
Prema legendi postojala je u drevnom Egiptu mitska zmija po imenu Ouroboros, koja je stavila svoj rep u usta i počela da ga jede i na taj način je postepeno potpuno progutala samu sebe. Mada je s biološke strane jasno da zmija to ne može da učini, matematičarima ovo nije bilo dovoljno već su odlučili da razmotre problem samoproždiruće zmije i sa čisto matematičke strane.

(Wikimedia)
Pretpostavimo da je početna dužina zmije 1 (u odgovarajućim jedinicama) i da je zmija na početku zauzela položaj kao na slici 1a. Pretpostavimo takođe da zmija uvek uzima oblik kruga sa centrom u koordinatnom početku i da joj se glava kreće isključivo u smeru kazaljke na satu.
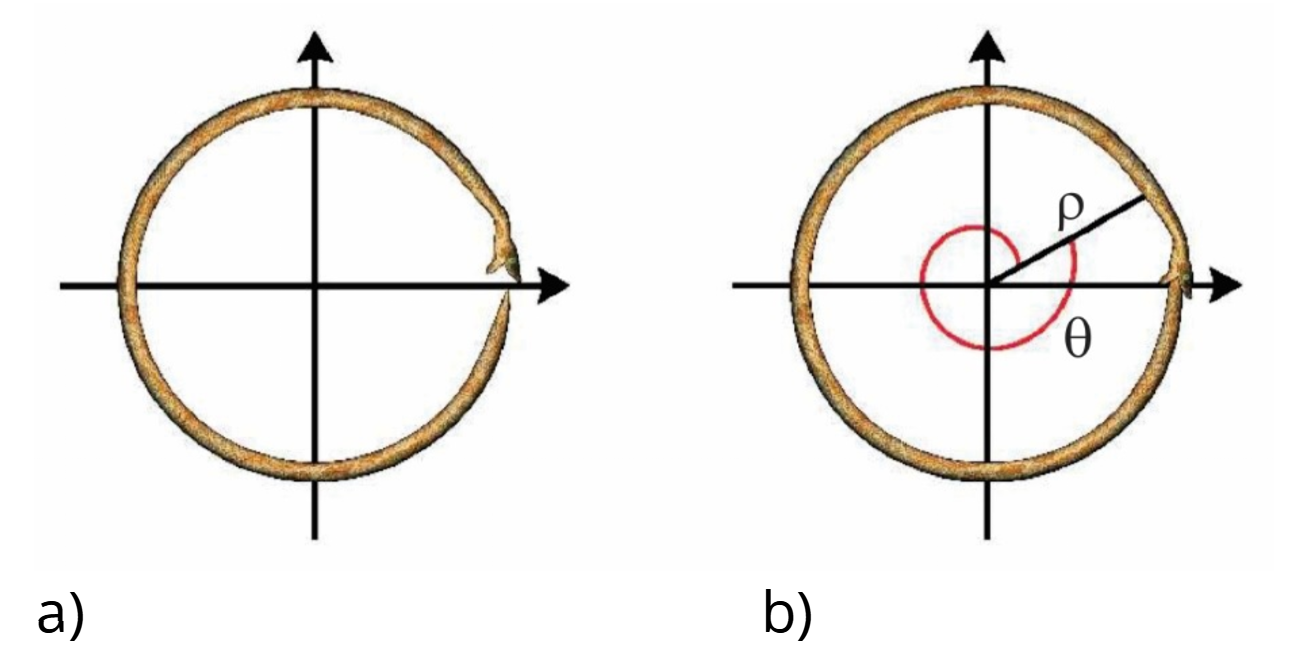
Sl. 1 Samoproždiruća zmija
Zmija počinje da jede svoj rep i posle nekog vremena izgleda kao na slici 1b. Neka je položaj kraja zmijinog repa izražen polarnim koordinatama, videti sliku 1b. Na početku je
![]()
a na kraju, kada zmija u potpunosti proguta samu sebe, imamo
![]()
Kako je na početku dužina zmije jednaka 1, biće
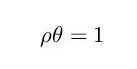
Putanja koju opisuje kraj zmijinog repa izražena je stoga kao
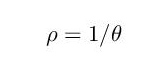
Da bismo ispitali da li zmija može u potpunosti da proguta samu sebe, koristićemo formulu za nalaženje dužine krive u polarnom koordinatnom sistemu
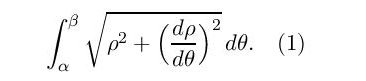
Sigurno da među čitaocima ima i onih koji nisu imali prilike da slušaju kurs „Primene integralnog računa” tako da im ova fomula izgleda strano, ali verujte da je tačna, izveo ju je holandski matematičar Hendrik van Horat još 1659. godine i niko u međuvremenu nije imao nikakvu primedbu.
Suštinski, čitaocima je bitna jedino informacija da li je dužina pomenute krive konačna ili beskonanačna, a kako se računa ova dužina nije cilj ovog priloga: naći će se neko ko to zna. Na kraju krajeva, ni najbolji svetski matematičari teško da su zapamtili sve matematičke formule i teoreme koje su učili na fakultetu. Američki psiholog i filozof R. F. Skiner jednom je izjavio: „Obrazovanje, to je ono što ostane nakon što zaboravite sve što ste naučili u školi”. Ova izreka se često neopravdano pripisuje Ajnštajnu. Ovom prilikom zgodno je pomenuti čuvenog italijanskog fizičara Enrika Fermija, dobitnika Nobelove nagrade za fiziku 1938. godine. Na pitanje jednog studenta kako se zove neka atomska čestica, odgovorio je: „Mladiću, da mogu da upamtim nazive svih tih čestica, bio bih botaničar”. A sličnim povodom francuski filozof i pisac Deni Didro je izjavio: „ Nisam toliko lud da bih znao sve”.
Dakle, primenjujemo formulu (1) i nalazimo dužinu krive koju opisuje kraj zmijinog repa
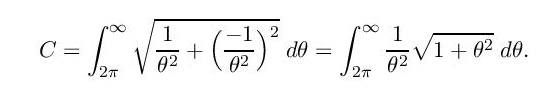
Ovaj integral nije baš lako izračunati, ali to neka vas ne brine, važan je samo krajnji rezultat. Utrenirani rešavači integrala (to su, između ostalih, studenti tehničkih fakulteta koji obavezno kažu da su rešili hiljadu integrala da bi položili „Matematiku I) bi sada uveli suptilnu ali ne i neočekivanu smenu
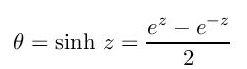
i izračunali
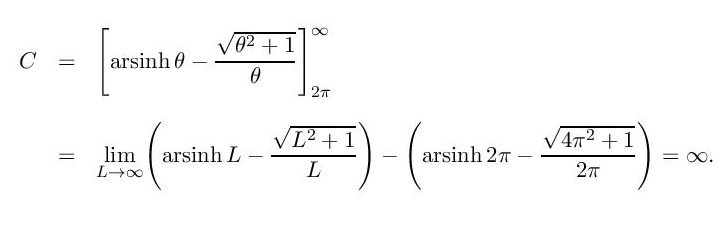
Dakle, kriva ima beskonačnu dužinu. Ovo znači da je nemoguće da zmija u potpunosti pojede samu sebe za neko konačno vreme jer, prema Ajnštajnu, kraj zmijinog repa ne može da se kreće brže od brzine svetlosti (a da zmija ne dobije ozbiljne stomačne bolove!).








