Interesantno je da naziv Hamiltonov put potiče od igre na dodekaedru (pravilni poligon koji ima 12 strana-pravilnih petouglova, 20 temena i 30 ivica, sl. 3) koji je postavio već pomenuti irski matematičar Vilijam Hamilton. Igra se prodavala pod imenom icosian (icosa – na grčkom dvadeset) ili Put oko sveta.

Prof. dr Miodrag Petković
Povremeno će se u ovoj rubrici u Galaksiji pojavljivati zanimljivi prilozi iz sveta matematike koji uključuju interesantne formule, događaje iz sveta matematike i života velikih matematičara i elementarne ali intrigantne i izazovne zadatke za čije rešavanje je dovoljno srednjoškolsko znanje matematike. Većina ovih priloga, i još matematičkih priča i zanimljivosti može se naći na sajtu www.miodragpetkovic.com, autora ovih priloga (opcija teme u meniju).
Trgovac planira da obiđe sve gradove u nekom regionu (državi ili i šire) ali tako da u svaki grad svrati jednom i samo jednom. I ako je moguće, da se vrati u polazno mesto. Bilo bi najbolje da ukupun put bude najkraći mogući. Ovako jednostavan (?!) plan doveo je do jednog od najtežih problema u matematici, a kako izgleda prema savremenim poznavanjima fizike, problem se ne može rešiti u opštem slučaju. U literturi on poznat kao „Problem trgovačkog putnika” (Travelling Salesman Problem, skraćeno TSP) i na ovu temu napisano je više hiljada i naučnih radova i knjiga.
Vilijam Rouvan Hamilton(Wikipedia)
Matematički prilaz prvi je dao u prvoj polovini 19. veka Vilijam Rouan Hamilton (1805-1865, Dablin, Irska), jedan od najvećih matematičara 19. veka, čije ime nose nekoliko pojmova i naziva u mehanici i matematici. Problem je od ogromnog praktičnog značaja i otuda veliko interesovanje za nalaženje bar približnog rešenja, što je naročito postalo aktuelno sa razvojem brzih računara, praćeno kreiranjem veoma efikasnih algoritama.
Matematički posmatrano, problem se može opisati na sledeći jednostavan način. Neka je u ravni zadat konačanskup od n nepreklapajućih tačaka A1,…An (sl. 1).Jedan od najvažnijih matematičkih problema, kako sa teorijskog, tako i sa praktičnog stanovišta, glasi: Obići sve tačke A1,…An mreže prolazeći kroz svaku tačku jednom i samo jednom.
Putevi kod kojih je moguć ovakav obilazak zovu se Hamiltonovi putevi. Zatvoren Hamiltonov put koji se završava u početnoj tački zove se Hamiltonova kontura. Hamiltonov put za konfiguraciju sa slike 1 prikazan je na slici 2. Ovo je i Hamiltonova kontura, jer je moguće iz poslednje tačke A9 doći u polaznu tačku A1
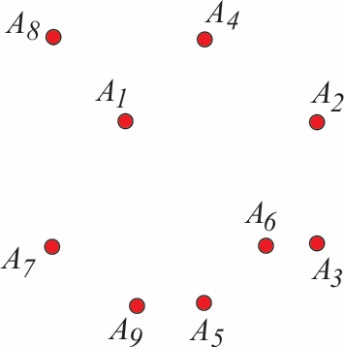
Sl. 1 Da li postoji Hamiltonov put?
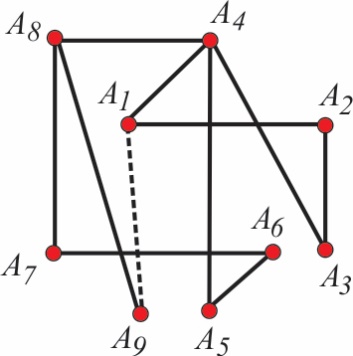
Sl. 2 Hamiltonov put za konfiguraciju sa slike 1
Tačke sa slike 1 mogu biti gradovi, aerodromi, čvorovi u arhitekturi mikroprocesora, vojne baze itd. Odavde je prilično jasno zašto su Hamiltonovi putevi od velikog interesa u mnogim primenama, kao što su telekomunikacione mreže, avio-saobraćaj, transport, dizajniranje mikroprocesora, razne logistike. Opšti algoritam (jednostavan ili komplikovan) za nalaženje Hamiltonovih puteva još uvek nije smišljen, i to je jedan od najtežih ali i najvažnijih nerešenih problema u teoriji grafova, teoriji optimizacije, teoriji računarskih nauka i, generalnije, u čitavoj matematici. Problem se ekstremno komplikuje akosetraži put minimalne dužine, tj. minimum sume
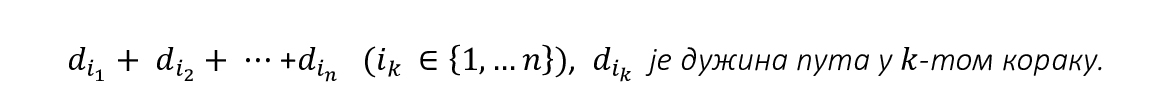
Dakle, ovde imamo dva problema: 1) potrebno je najpre naći sve Hamiltonove puteve (ako uopšte postoje, i ako postoje, odrediti ih) i 2) odrediti Hamiltonov put minimalne dužine. Umesto minimalne dužine, kao kriterijum se može zadati i minimalno utrošeno vreme puta, najniži troškova puta i slično.
Čak i ako broj objekata n nije veliki (recimo 100), ni današnji superračunari ne mogu egzaktno da reše ovaj problem jer vreme izvršenja raste više nego eksponencijalno, otprilike reda n! gde n! označava proizvod svih prirodnih brojeva od 1 pa zaključno do n. Recimo, 4!=24, 10! =3 628 800, a 50! je broj koji se piše sa 64 cifre. Zamislite problem optimalnog avio-saobraćaja u SAD koja ima oko 5.000 civilnih aerodroma. Još 1995. godine jedna velika američka avio-kompanija ponudila je nagradu od 20 miliona dolara za skoro optimalno rešenje (nije baš sasvim jasno šta se pod tim podrazumevalo). Nagradu nije niko dobio.
U broju 3/2020 štampanog izdanja „Galaksije” profesor Mirko Vujošević je u članku „Arijadnin trag” opširno pisao o TSP. Naglašeno da TSP pripada grupi najtežih optimizacionih problema za koji se ni izbliza ne nazire rešenje u opštem slučaju, a eksperti veruju da ni računari milijardu milijardi puta brži od današnjih super računara ne mogu da reše svaku konfiguraciju jer ni vreme mereno milijardama godina nije dovoljno.
Interesantno je da naziv Hamiltonov put potiče od igre na dodekaedru (pravilni poligon koji ima 12 strana-pravilnih petouglova, 20 temena i 30 ivica, sl. 3) koji je postavio već pomenuti irski matematičar Vilijam Hamilton. Igra se prodavala pod imenom icosian (icosa – na grčkom dvadeset) ili Put oko sveta.
Naći put po ivicama dodekaedra koji kroz svako teme dodekaedra prolazi jednom i samo jednom. Do rešenja se lako dolazi ako se dodekaedar predstavi preko svoje stereografske projekcije u ravni, tzv. skeletona dodekaedra. Jedna Hamiltonova kontura duž skeletona prikazana je na slici 9 pomoću podebljanih linija u crvenoj boji.
Sl. 3 dodekaedar
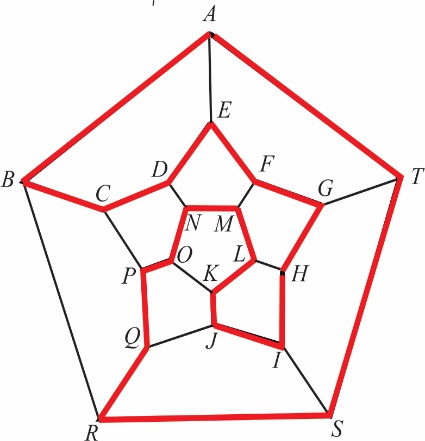
Sl. 4 Hamiltonova kontura
Pomenuli smo da je Hamiltonov put na dodekaedru često popularno opisivan kao Put oko sveta. Koristeći moćni programski paket Mathematica koji je osmislila (i dalje usavršava) kompanija Wolfram (na čelu sa idejnim tvorcem Stivenom Volframom), moguće je napraviti simulaciju Puta oko sveta, pri čemu se zaista obilaze glavni gradovi svih država sveta (po konturi koja aproksimira Hamiltonovu). Pri ovome se koristi baza CountryDatakoju poseduje ovaj softver i aplikacija Graphics3D za crtanje. Skica putanje može se videti na Volframovom linku:
Evo još jednog čuvenog primera (iz arapskih spisa, 9. vek) iz rekreativne matematike: Put koji šahovska figura skakač napravi na standardnoj šahovskoj tabli 8x8 tako da obiđe sva 64 polja, prelazeći preko svakog polja jednom i samo jednom, i pritom se vraća na polazno polje, čini Hamiltonovu konturu.
Ovim problemom bavili su se čuveni matematičari Ojler, Vandermond, Ležandr, De Muavr, De Monmor i drugi.Na slici 5 prikazano je Ojlerovo rešenje iz 1757. (u vreme kada je bio potpuno slep).
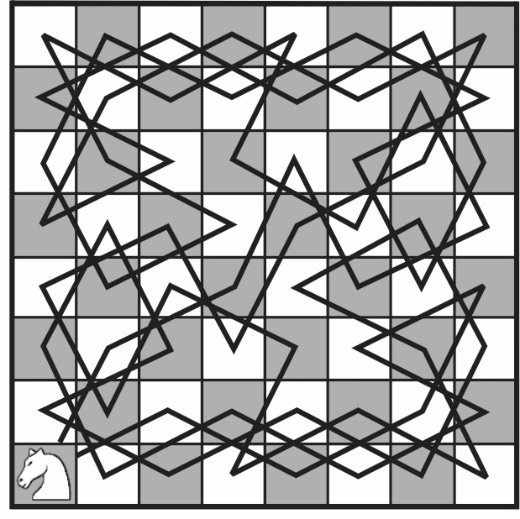
Sl. 5 Ojlerovo rešenje skakačeve
Hamiltonove konture
Dodajmo na kraju interesantu priču o Hamiltonovom opredeljenju za matematiku. Kao dečaka, ujak lingvista ga je usmeravao na učenje stranih jezika. Hamilton je bio čudood deteta: u petoj godini čitao je knjige na grčkom ihebrejskom jeziku; takođe je mogao da pišena francuskom iitalijanskom; u desetoj je učio arapski i sanskrit; udvanaestoj već je dobro znao ove jezike, zajedno sa sirijskim,persijskim, hindu i malajskim.
Prekretnica u njegovom životunastala je kada je imao dvanaest godina, posle susreta sa američkim„živim kalkulatorom” Zirom Kolbernom. Zira Kolbern jemogao da izvodi napamet komplikovana aritmetička izračunavanja i Hamilton je odlučio da oproba svoje sposobnosti utakmičenju sa njim. Ispostavilo se da je poraz od Kolbernaprobudio kod Hamiltona veliki interes za matematiku, kojoj seodmah posle toga potpuno posvetio.








