U ovom kratkom prilogu bavimo se temama u vezi sa neprekidnim funkcijama i njenim osobinama. Razmatrana je tzv. Palačinka teorema, a zatim dva jednostavna zadatka, temperature na ekvatorskoj liniji i put planinara. Uslovno rečeno jednostavni jer rešenja zahtevaju suptilne ideje. Oba zadatka su često sastavni deo testiranja u IT kompanijama.

Prof. dr Miodrag Petković
Iz matematičke analize dobro je poznato tvrđenje.
Teorema 1.Ako neprekidna kriva definisana jednačinom y = f(x) ima minimalnu vrednost A i maksimalnu vrednost B na intervalu definisanosti [a,b], tada funkcija f mora uzeti svaku vrednost između A i B.
Ovo tvrđenje je intuitivno jasno na osnovu grafika funkcije f na [a,b], slika 1. U ovom prilogu upotrebićemo teoremu 1 da dokažemo jedan interesantan rezultat u literaturi poznat i kao palačinka teorema.
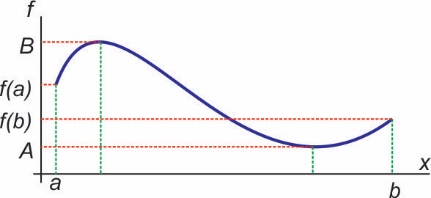
Sl. 1 Neprekidna funkcija (uz teoremu 1)
Podela zatvorene ravanske oblasti
Posmatrajmo oblast u ravni ograničenu zatvorenom linijom koja ne seče samu sebe. To može da izgleda kao palačinka (sl. 2) pa otuda i naziv gore pomenute teoreme. Pitanje glasi: Da li se ova oblast može podeliti pravom na dva dela jednakih površina i to polazeći iz bilo kog pravca?
Odgovor je pozitivan: može. Da bismo to dokazali, najpre povucimo pravu X izvan oblasti (palačinke) F pod proizvoljnim uglom (ovim je definisan proizvoljan pravac pomenut u zadatku), videti sliku 2. Neka je površina oblasti F jednaka PF.
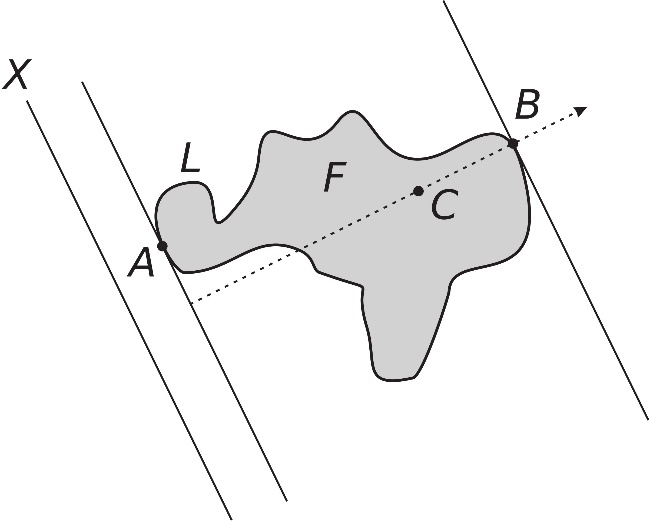
Sl. 2 Palačinka teorema
Označimo sa PF(C) površinu isečenu od figure F pravom koja prolazi kroz unutrašnju tačku C (sl. 2). Pomerajmo pravu X prema graničnoj konturi L oblasti F zadržavajući isti ugao sve dok X ne dodirne liniju L u tački A. U ovoj startnoj poziciji nijedan deo figure F nije pokriven, prema tome imamo da je PF(A) = 0. Prava X zatim nastavlja od tačke A da seče figuru F. Jasno je da u tačkama C unutar oblasti F važi PF(C) > 0. Prava X izlazi iz oblasti F u tački B, tada je oblast F potpuno prekrivena i imamo da je PF(B)=PF. Vrednost PF(C) neprekidno raste dok se prava X pomera od ulazne tačke A do izlazne tačke B uzimajući sve vrednosti od 0 do PF. Na osnovu teoreme 1 sa početka teksta, u jednoj poziciji tačke C* mora biti PF(C*) = PF/2, što potvrđuje da postoji rešenje postavljenog zadatka. Ovim smo dokazali palačinka teoremu.
Teorema 2.Oblast u ravni ograničena zatvorenom linijom koja ne seče samu sebe može se podeliti pravom na dva dela jednakih površina i to polazeći iz bilo kog pravca.
Štaviše, na osnovu dokaza gornje teoreme sledi da se od oblasti F uvek može odrezati oblast čija je površina jednaka n-tom delu površine oblasti F jer u nekoj tački C** biće PF(C**) = PF/2. Primetimo da izložena diskusija ne daje odgovor o poziciji tačke C*.
Temperatura na ekvatoru
Sledeći interesantan zadatak se rešava koristeći upravo izložen koncept neprekidnosti.Dokazati da na ekvatorskoj liniji postoje dve dijametralno suprotne tačke u kojima su temperature jednake.
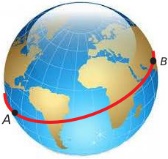
Sl. 3 Temperatura na ekvatoru
Rešenje: Posmatrajmo na ekvatoru međusobno suprotne tačke A i B u kojima je temperatura redom TA i TB, slika 3. Bez gubljenja opštosti možemo da pretpostavimo da razlika TA-TB ima pozitivnu vrednost. Pustimo sada da tačke A i B rotiraju istovremeno po ekvatorskoj liniji zadržavajući njihovu opoziciju, sve dok ne zamene mesta. Temperature TA i TB tačaka A i B se sve to vreme menjaju i u novom položaju imamo da je TA-TB < 0 jer tačka A je zauzela mesto tačke B (koja je hladnija). S obzirom da je razlika TA-TB od pozitivne vrednosti (pre početka kretanja po ekvatorskoj liniji) postala negativna posle završenog polukružnog kretanja, zbog kontinualne promene temperaturne razlike, u nekom momentu ova razlika je morala da bude jednaka nuli. Taj momenat određuje pozicije suprotnih tačka na ekvatoru u kojima je temperatura jednaka.
Planinarov put
Koristeći isti princip, može se rešiti i sledeći interesantan zadatak koji je zadavao muke i univerzitetskim profesorima iako je rešenje vrlo jednostavno – naravno, ako se ima prava ideja:Jednog dana, tačno u 6 ujutru, planinar je počeo da se penje uskom stazom koja je spiralno vodila do planinarskog doma na vrhu planine. Planinar je išao neravnomernom brzinom, često se odmarajući na svom putu. Na vrh planine stigao je pred zalazak sunca. Pošto je prespavao u planinarskom domu, sutradan ujutru je u 6 sati krenuo niz planinu. Spuštao se istom stazom i išao neravnomernim korakom, povremeno se odmarajući. Dokazati da postoji tačka na stazi u koju će on dospeti prilikom spuštanja tačno u isto vreme kao i prethodnog dana dok se penjao uz planinu.
Za rešavanje ovog zadatka nije potrebno nikakvo matematičko znanje. Pre izlaganja rešenja za nestrpljive čitaoce dajemo pauzu za osveženje u vidu lepog planinskog pejzaža. Oni uporniji mogu da zaposle svoj mozak tražeći ideju za rešavanje zaustavljajući se kod donje slike. Rešenje sadrži vrlo jednostavnu ali i efektnu ideju i ponovo je zasnovano na principu kontinuiteta.

(Vladimir Petković)
Rešenje: Pretpostavimo da u planinarenju učestvuju dva planinara: jedan koji je u 6 ujutru počeo da se penje uz planinu, i drugi koji je u isto vreme i istom stazom počeo da se spušta niz planinu. U nekom momentu oni se moraju sresti na stazi; tačka susreta je upravo tražena tačka jer je od vremena polaska obojice planinara proteklo isto vreme.








