U teoriji verovatnoće „paradoks rođendana” ili „problem rođendana”, poznat i pod nazivom „paradoks blizanaca”, tvrdi da u grupi od 23 slučajno odabranih ljudi, šansa da postoji bar jedan par osoba koji ima rođendan istog dana, iznosi oko 50 procenata. Zbog ovog neočekivanog ishoda problem se i naziva „paradoksom rođendana”. U svarnosti, matematički je sve apsulutno korektno, osim iznenađujućeg rešenja tako da paradoksa, u stvari, i nema.

Prof. dr Miodrag Petković
Povremeno će se pod ovim naslovom u pojavljivati zanimljivi prilozi iz sveta matematike koji uključuju interesantne matematičke formule, događaje iz sveta matematike i života velikih matematičara, a i elementarne ali intrigantne i izazovne zadatke za čije rešavanje je dovoljno srednjoškolsko znanje matematike. Većina ovih priloga, i još matematičkih priča i zanimljivosti može se naći na sajtu www.miodragpetkovic.com, autora ovih priloga (opcije teme u meniju).
Da ne bi došlo do zabune, napomenućemo da se u teoriji verovatnoće „paradoks rođendana” ili „problem blizanaca” o kome će biti reči, ne odnosi na efekat koji se u literaturi, takođe, zove „paradoks blizanaca” koji ima veze s vremenskom dilatacijom kao posledicom teorije relativnosti. Podsetimo, ako jedan od dvojice kosmonauta-blizanaca putuje raketom brzinom bliskom brzini svetlosti, posle izvesnog broja godina provedenog u svemiru vraća se na Zemlju znatno mlađi nego njegov brat – putniku je vreme sporije proticalo, tako kaže Ajnštajnova teorija relativnosti. U našoj priči radi se o prizemnom događaju.
Na zabavi se okupilo veliko društvo, svira muzika i svi se lepo zabavljaju, ali vama je dosadno. Onda ste se setili da se malo razdrmate jednom malom anketom i krenete od osobe do osobe sa istim pitanjem: kojeg datuma u godini imaju rođendan? Koliko najmanje osoba treba da pitate da biste s verovatnoćom od bar 50%, tj. većom od 1/2, dobili isti odgovor, tj. da među prisutnim postoje bar dve osobe sa istim rođendanom? Problem je postavio američki matematičar (rođen u Austriji) Rihard fon Mizes 1939.
Verovatno zamišljate neki ne tako mali broj, recimo 50 ili 100, međutim, kao što ćemo videti, taj broj je 23. Zbog ovog neočekivanog rešenja problem se i zove „paradoks rođendana”. Rešavajući ovaj problem treba eliminisati prestupnu godinu i pretpostaviti da se bilo koji dan u godini može pojaviti kao rođendan, dakle s verovatnoćom 1/365. Takođe pretpostavljamo da na zabavi nema blizanaca. Uzgred da napomenemo da je prema nekim izvorima inicijalna kapisla da fon Mizes formuliše ovaj problem bila koincidencija datuma rođenja dve slavne ličnosti: 12. februara 1809. rođeni su američki predsednik Abraham Linkoln i čuveni engleski biolog Čarls Darvin.
Kako smo došli do broja 23? Označimo s verovatnoću da dve osobe nemaju rođendan istog dana, a sa P suprotan događaj – dve osobe imaju rođendan istog dana. Zamislimo da su svi gosti u dvorištu i da, jedan po jedan, ulaze u prostoriju za zabavu. Potražimo verovatnoću da među prisutnima koji ulaze nema podudaranja rođendana. Kada prva osoba uđe, verovatnoća da njen rođendan nije isti kao i nekog od prisutnih je naravno 1 jer u prostoriji nema nikog. To možemo da zapišemo u obliku razlomka
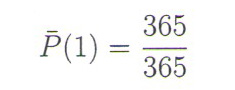
jer je brojilac 365 broj svih povoljnih mogućnosti, a imenilac 365 je broj svih mogućih ishoda.
Kada druga osoba uđe, njen rođendan mora da bude različit od osobe koja je prethodno ušla, tako da imamo 364 povoljna izbora od 365. Verovatnoća da ove dve osobe imaju različite rođendane je
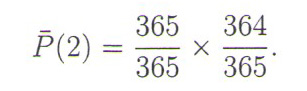
Kada treća osoba uđe, verovatnoća nepoklapanja rođendana za ove tri osobe jednaka je
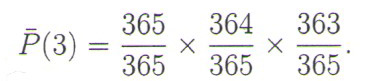
Na osnovu prethodnog, način izračunavanja verovatnoće različitih rođendana je jasan. Posle ulaska k osoba, verovatnoća za k različitih rođendana je
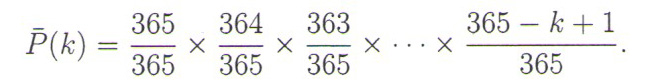
Verovatnoća da bar dvoje prisutnih ima rođendan istog dana jednaka je suprotnoj verovatnoći, tj.
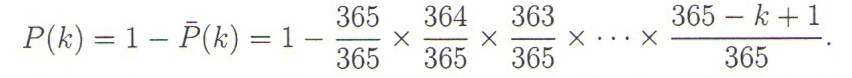
Da bismo odgovorili na postavljeno pitanje, potrebno je pronaći najmanje k za koje verovatnoća P(k) postaje veća od 1/2. Svaki od razlomaka u gornjem proizvodu, osim prvog, manji je od 1, tako da P(k) očigledno raste sa porastom k i za neko k mora preći granicu od 1/2, videti sliku u nastavku priloga.
Prvo k=k* za koje je
![]()
daje traženo rešenje, gde smo sa P1/2 (n) označili kritičnu verovatnoću veću od 1/2 u slučaju n (teorijski) mogićih ishoda (365 dana). U našem slučaju je k*=23 i dobijamo
![]()
Primetimo da je P(22)=0.492703, dakle nešto ispod 1/2. Prema tome, traženi minimalni broj je 23. Dakle, možete se kladiti sa šansm od bar 50% da se među 23 osobe nalaze bar dve sa istim rođendanom!
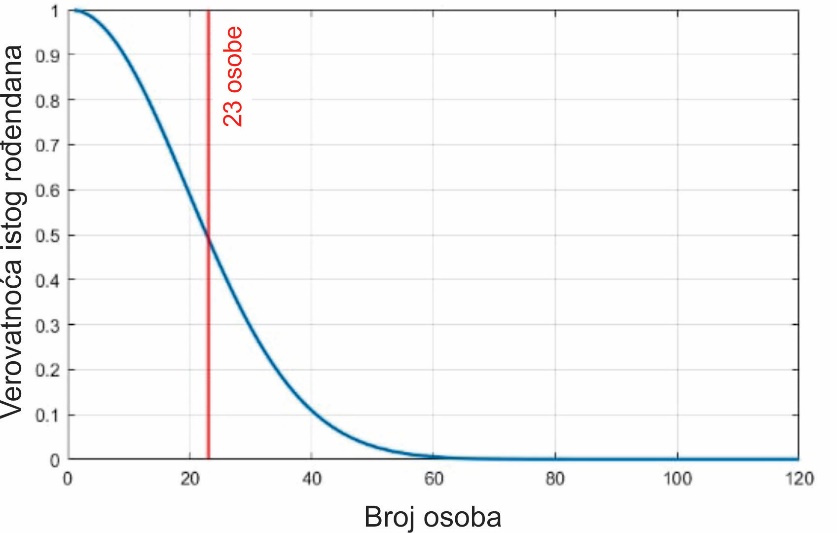
Dobijeni broj izgleda zaista neočekivano mali, ali ne zaboravimo da su ovde u pitanju kombinacije bilo kog para osoba među prisutnim; ovo je suštinski različito od pitanja koliko osoba treba pitati da bi se utvrdilo s verovatnoćom većom od 1/2 da neki od njih imaju isti rođendan kao neka konkretna osoba, na primer baš vi. Odgovor je znatno veći broj – čak 253. Na slici je prikazana verovatnoća istog rođendana kao funkcija broja anketiranih osoba.
Zanimljivo je napomenuti da se diskutovani efekat „blizanaca” javlja kod kriptografskih sistema koji koriste jednu vrstu tzv. haš (hash) funkcija pri transferu poruka. Ako bi neki haker pokušao da dešifruje poruku koju je poslao kriptosistem koristeći haš funkciju u 64-bitnom sistemu tako što bi slučajnim izborom došao do n podataka, da bi ostvario svoj cilj s verovatnoćom ne manjom od 0,5 bilo bi mu potrebno oko 1019podataka (deset milijardi milijardi). Ako bi haker koristio moderan PC (recimo sa „Intelovim” procesorom i7 devete generacije), bilo ni mu potrebno oko 1.000 godina za ovaj pokušaj.
Analiza korišćena pri razmatranju „problema rođendana” može se primeniti na situaciju u kojoj neko sluša pesme sa MP3 plejera koji sadrži 1.000 pesama. Ako plejer emituje pesme slučajnim izborom sa spiska (ili kako se to kaže, plej-liste), posle koliko pesama sa verovatnoćom od bar 0,5 će se ponoviti neka pesma (ne neka određena, već bilo koja)?
Pre svega, recimo da to zavisi od toga šta se podrazumeva pod „slučajnim izborom”. Većina plejera ili MP3 programa na računarima, mobilnim telefonima i tabletima pakuje pesme sa liste na isti način na koji se pakuju (mešaju) karte pre igre. Kada su jednom spakovane, sve pesme se emituju redom i nema ponavljanja sve do 1.001 pesme, dakle sve dok se lista od 1.000 pesama ne iscrpi. Ako se program prekine opcijom „ponovno pakovanje” (re-shuffling) i opet izvrši pakovanje (shuffling), pesme će biti emitovane u nekom drugom redu, ali opet bez ponavljanja.
Pretpostavimo sada da imamo MP3 plejer i plej-listu sa 1.000 pesama i da se svaka pesma bira slučajno prilikom svakog emitovanja (tzv. suffleׅ ili random opcija). Kao u slučaju „paradoksa rođendana”, posle k pesama verovatnoća da neće doći do ponavljanja neke od pesama jednaka je
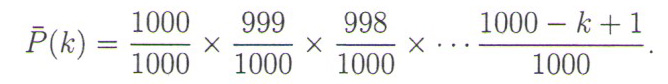
Suprotna verovatnoća da će se ponoviti bar jedna pesma sa verovatnoćom većom od 1/2 je
![]()
Očigledno je da verovatnoća P(k) raste s porastom k i opet tražimo najmanje k=k* za koje verovatnoća prelazi 1/2. U našem slučaju je k*=38 i dobijamo
![]()
Primetimo da je P(37)=0,490464, dakle ispod 1/2.
Može se pokazati (ovu analizu preskačemo u ovom prilogu) da je u problemima koje smo razmatrali približna procena za k* kada postaje P(k*)>1/2 u slučaju velikog broja n data sa
![]()
Za razmatranu plej-listu od n=1.000 pesama dobija se na ovaj način 37,23. Procena (u odnosu na tačnu vrednost k*=38) se može smatrati zadovoljavajućom jer je greška samo 2%.
Iz ove priče može se zaključiti da je pri rešavanju zadataka iz verovatnoće veoma važno shvatiti precizno kompleks uslova pod kojima se traži verovatnoća realizacije nekog događaja. Kao što je naglašeno na početku, događaj da dve konkretne osobe na nekoj velikoj zabavi imaju rođendan istog dana u godini je suštinski različit od događaja da bar dve osobe (bilo koji par) imaju rođendan istog dana. Za prvi događaj se može reći da je vrlo redak, jer je verovatnoća da se desi prilično mala, dok je drugi skoro običan.
Sledeći kratak prilog ilustruje da redak događaj itekako može biti od izuzetnog, bolje reći, od životnog značaja. Razmotrimo tvrđenje naučnika da je upravo niz izuzetno retkih događaja i specifičnih (pogodnih) uslova doveo do uspona života na Zemlji. Na primer, bez proteina ne bi bilo života na Zemlji. Oni se sastoje od aminokiselina poređanih po određenom redosledu. Kolagen, jedan tip proteina, predstavlja lanac od 1.055 aminokiselina u tačno određenom nizu, a šansa da se to desi je 1/10260 (imenilac se piše sa 260 cifara). Koliko je to veliki broj pomenimo da se procenjuje da u (trenutno) poznatom svemiru ima između 1078 i 1082 atoma.
Skoro da se može zaključiti da po zakonima verovatnoće proteini ne bi trebalo da postoje. Čuveni astronom Fred Hojl je izglede za formiranje proteina uporedio s konstrukcijom džambo-džeta od delova aviona nasumično uzetih sa otpada. A ipak se čuda dešavaju, u slučaju proteina to se zove čudo života.








