Jednačine u kojima se traži da rešenja budu celi ili racionalni brojevi (tzv. Diofantove jednačine) često imaju jednostavnu formu ali mogu biti veoma teške za rešavanje. Na ovom mestu je razmatrano nekoliko interesantnih primera, pri čemu se kao teme javljaju i takva pitanja kao što su suština života i univerzuma sa gledišta galaktičkih superračunara, superračunar sastavljen od 500 000 umreženih računara i greške čuvenih matematičara.

Prof. dr Miodrag Petković
Godine 1954. na Univerzitetu u Kembridžu među matematičarima je kružilo ovo pitanje: „Koji brojevi od 1 do 100 mogu da se predstave kao suma tri kuba celih brojeva?” Rečeno algebarskim jezikom, treba rešiti jednačinu
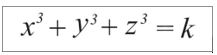
gde je k bilo koji broj iz skupa {1,2,…,100}, a x, y i z celi brojevi.
Pretpostavlja se da je ovaj zadatak postavljen još u 3. veku od strane grčkih matematičara i jasno je da se tada odnosio samo na prirodne brojeve jer su negativni brojevi bili nepoznati. Gornji problem je poznat pod nazivom „suma tri kuba”. Jednačine u kojima se traže rešenja u skupu celih brojeva (i opštije, u skupu racionalnih brojeva – racionalan broj je količnik dva cela broja) nazivaju se Diofantove jednačine po matematičaru Diofantu iz Aleksandrije koji je razmatrao ovaj tip jednačina pre oko 1.800 godina. Nakon publikovanja pomenutog zadatka matematičari su pedesetih godina prošlog veka vrlo brzo našli rešenja za male brojeve k. Mogućnost da se na levoj strani jednačine mogu javljati i negativni brojevi, dovodi do velikih komplikacija i bez računara više ništa nije moglo da se uradi. Veliki broj matematičara i programera radi na ovom problemu više od pola veka tako da je postao opšte popularan i atraktivan za širu publiku. Pokazano je da se neki brojevi ne mogu predstaviti kao suma tri kuba kao što su 4, 5, 13, 14, 22, 23, 31, 32, svi manji od 33. U aprilu 2019. profesor Endru Buker sa Univerziteta u Bristolu, u Engleskoj, pomoću računara koji je radio nekoliko nedelja, pronašao je relaciju za k=33 koja glasi

Sam pogled na ove veoma velike brojeve pokazuje koliko je ovaj problem težak.

Tada su se u priču umešali fanovi kultne naučnofantastične serije „Autostoperski vodič kroz galaksiju” (The Hitchhiker’s Guide to the Galaxy), pisca, scenariste, glumca i gitariste Daglasa Adamsa (osim knjige, snimljena je i TV serija, radio-drama i film (2005) i pitali da li postoji rešenje zadatka sa početka priloga za broj 42. Zašto baš broj 42? U pomenutoj knjizi, prodatoj u 15 miliona primeraka, opisano je kako par naučnika postavlja pitanje najvećem superračunaru u galaksiji o suštinskom smislu života, svemira i svačega. Nakon 7,5 miliona godina efektivnog rada, računar daje odgovor:

(Ilustracija Vladimir Petković)
Zbunjeni ovim odgovorom, naučnici su u dalekoj budućnosti tražili objašnjenje od računara šta odgovor 42 zapravo znači, našta im je računar rekao da bi oni ovaj odgovor shvatili da su njihovi prethodnici pravilno postavili pitanje. Računar je obećao naučnicima da će napraviti još moćniji računar koji će znati kako glasi konačno pitanje koje odgovara konačnom odgovoru; računar će nositi naziv Earth (Zemlja).
Inače, Adams je superračunar nazvao Deep Thought (Duboka misao), a tako je nazvan i prvi računar koji je igrao šahovski meč 1996. sa (tadašnjim) svetskim prvakom Garijem Kasparovim (i izgubio). Dizajner ovog računara (pre svega specijalnog mikroprocesora) jeste Tajvanac Feng-Hsiang Hsu, u to vreme doktorand na Unuverzitetu Karnegi Melon u Pitsburgu, koji je kasnije bio i tvorac superračunara Deep Blue (uz veliku tehničku i finansijsku pomoć IBM-a, koji je 1997. pobedio istog svetskog prvaka u šahu. Glavni savetnik bio mu je mentor za doktorsku disertaciju Hsiang Kung, takođe Tajvanac, matematičar i jedan od vodećih naučnika u kompjuterskim naukama, pionir u oblasti paralelnih računara i sistoličkih polja. Godine 2009. imao sam posebnu čast da budem njegov gost na Univerzitetu Harvard i, osim matematičkog istraživanja, u razgovoru čujem mnoge interesantne činjenice o konstrukciji Hsuovih računara.

Feng-Hsiang Hsu Autor članka i profesor Hsiang Kung
Vreme je da se vratimo glavnoj temi. Bristolski profesor Endru Buker je ponovo pokrenuo svoj program ali ni iscrpnom pretragom nije našao rešenje za k=42 . Međutim, pokazao je da, ako rešenje postoji, brojevi x, y , i z moraju biti van intervala [A, A] , gde je A broj veći od 1015. Rad sa ovako velikim brojevima bi zahtevao stotine godina računarskog vremena i zato je Buker potražio pomoć imenjaka Endrua Saterlenda, profesora sa Masečusetskog instituta za tehnologiju (MIT), koji je bio poznat po paralelnom procesiranju na ogromnoj globalnoj računarskoj mreži Charity Engine. Ova mreža povezuje 500.000 računara širom sveta i to je svetski rekord u broju umrežavanja. Septembra 2019. ovaj supersuperkompjuter posle milion sati vremena pretraživanja pronašao je rešenje:

Naravno, treba pomenuti da pri ovom rešavanju nije primenjena gruba sila (brute force) već vrlo sofisticiran algoritam razvijen na MIT-u.
To bi, bez velike pompe i slavlja, bio odgovor na smisao života, univerzuma i svega, po Adamsu (ili po „Dubokoj misli”). Ko želi, može da prihvati zagonetan odgovor, a matematičari i programeri su uradili ono što se od njih tražilo. Možda treba da budemo srećni što, za razliku od Adamsove potrage za istinom, Zemlja nije uništena u tom procesu.
Još ponešto o Diofantovim jednačinama. Ovaj tip jednačina često je zadat pomoću jednostavnih relacija, ali odgovor može da bude veoma težak. Još 1637. francuski matematičar i pravnik Pjer Ferma tvrdio je, bez dokaza, da za proizvoljna tri prirodna broja x, y i z i n>2 važi

(Takozvana Fermaova poslednja teorema). Tek 357 godina kasnije, 1994, dokaz je dao britanski matematičar Endru Vajls (već treći Endru u ovom prilogu) posle osam godina napornog rada.

Pjer Ferma, Endru Vajls
Razmatrajući Diofantove jednačine, teško je ne pomenuti dve kratke priče o greškama dvojice velikih matematičara.
Jedan od najvećih svih vremena, Leonard Ojler, tvrdio je da nijedan n-ti stepen ne može biti suma manje od n-tih stepena prirodnih brojeva. Očigledno je ovo važi za n=2 ali takođe i za n=3 , jer se ovaj specijalan slučaj svodi na Fermaovu poslednju teoremu. Međutim, 1966. godine, dva veka nakon što je Ojler postavio ovu hipotezu, Leon Lander i Tomas Parker su pronašli kontraprimer pomoću računara. Ovaj kontraprimer je pronađen za n=5 i glasi
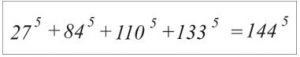
Kao što se može videti, peti stepen je izražen kao zbir samo četiri sabiraka podignutih na peti stepen.
Drugi primer govori o trijumfu matematičara-amatera nad čuvenim matematičarem. Jedan problem, postavljen u 19. veku, sastojao se u nalaženju dva pozitivna racionalna broja čiji je zbir kubova jednak 6. Veliki francuski matematičar Adrien Mari Ležandr dao je „dokaz nemogućnosti” takve reprezentacije. Međutim, nekoliko decenija kasnije, početkom dvadesetog veka, čuveni britanski sastavljač matematičkih zagonetki, rebusa i drugih glavolomki, Henri Dudeni (1857-1930), oborio je njegov dokaz i dao vrlo jednostavno rešenje
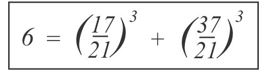
Problem koji je rešavao Ležandr bio je dečja igra za Dudenija u poređenju sa sličnom reprezentacijom dva pozitivna racionalna broja čija suma kubova iznosi 9, a da pritom to nije par (1,2). On je pronašao da razlomci

zadovoljavaju traženi uslov. Njegovo rešenje zaslužuje iskreno divljenje ako se uzme u obzir da nije posedovao nikakvu računsku mašinu. Inače, ovaj problem se lako svodi na jednačinu
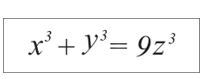
gde su x i y brojioci, a z imenilac gornjih razlomaka. Očigledno je da za x=1, y=2, z=1 gornja relacija važi, ali je u zadatku ovo rešenje isključeno kao trivijalno. Jedno od rešenja je Dudenijevo rešenje koje sledi na osnovu gornjih razlomaka.

Nije poznato da li ima drugih rešenja. Ovo je i izazov za vrhunske matematičare i programere da ispitaju da li postoji bar još jedno rešenje (ZADATAK 1). Upozorenje: Ne pokušavajte da primenite grubu silu, biće vam potrebno nekoliko milijardi godina čak i sa najbržim računarom! Na početku smo pomenuli pretpostavku da je problem „suma tri kuba” bio poznat u staroj Grčkoj. To ostaje da se i dalje nagađa ali ono što je sigurno jeste da su znali za vrlo interesantnu relaciju u kojoj učestvuju 4 uzastopna prirodna broja
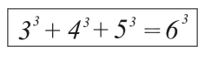
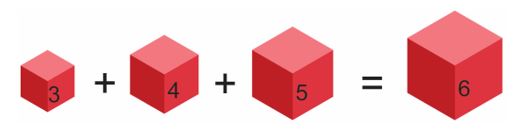
Ova relacije daje ideju za jedan zanimljiv, izazovan ali i težak ZADATAK 2: Date su tri drvene kocke sa ivicama 3, 4 i 5. Koristeći što manje sečenja ovih kocki, od dobijenih delova sastaviti kocku ivice 6.
Čitaoci koji prvi reše bar jedan od dva zadatka dobiće kao nagradu knjigu iz popularne matematike (dva zadatka – dve knjige). Rok: 31. decembar 2019.








