U geometriji Pikova teorema daje vrlo jednostavnu formulu za izračunavanje površine prostog poligona (poligona koji nema „rupa” i čije se stranice ne seku), čija su temena zadata celobrojnim koordinatama. Izračunavanje se svodi na prebrojavanje tačaka u unutrašnjosti poligona i na njegovim granicama. U prilogu su date dve interesantne primene Pikove teoreme.

Prof. dr Miodrag Petković
Nacrtajmo na listu papira vertikalne i horizontalne linije tako da obrazuju mrežu jednakih kvadrata sa stranicom 1. Uzmimo zatim temena kvadrata za temena poligona čije se stranice ne presecaju, kao na slici 1. Pikova teorema nam kaže da se površina A ovog poligona može izračunati prebrojavanjem broja U tačaka koje se nalaze unutar poligona i broja G tačaka koje formiraju granicu poligona na sledeći način: A = U + G/2 – 1. Britanski pisac Dejvid Darling napisao je da „Pikova teorema predstavlja vezu između tradicionalne euklidske geometrije i moderne digitalne (diskretne) geometrije”.
Ako je stranica kvadrata jednaka a, lako se pokazuje da je površina jednaka
A = (U + G/2 – 1) S=(U + G/2 – 1) a2, gde je S površina kvadrata iz pomenute mreže.
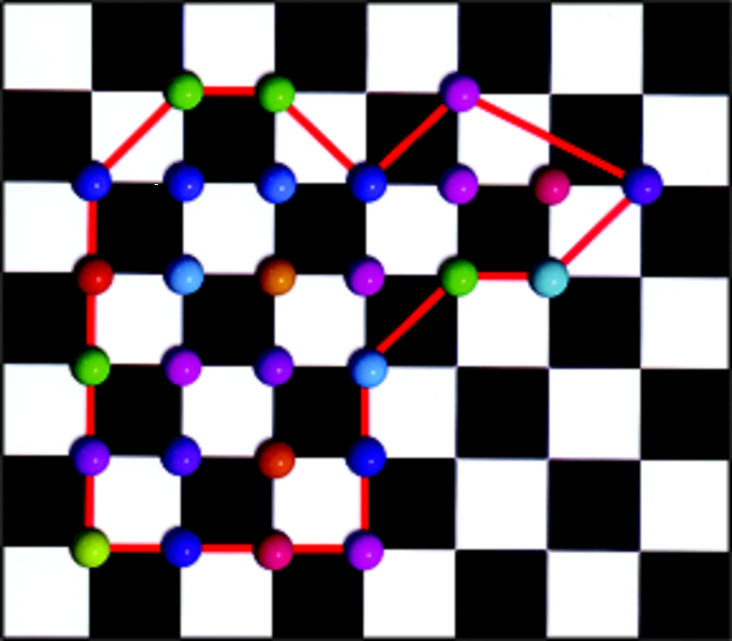
Sl. 1 Ilustracija Pikove teoreme
Austrijski matematičar Georg Pik (Pick, 1859-1942) formulisao je ovu teoremu 1899. Pik je poznat i po tome što je upoznao Alberta Ajnštajna sa matematičarima koji su mu pomogli (u matematičkom delu) u radu na opštoj teoriji relativnosti. Nažalost, Pik je doživeo tragičnu sudbinu. Budući da je bio Jevrejin, pred Hitlerovom okupacijom Austrije 1938. pobegao je u Prag, ali je posle okupacije Čehoslovačke bio uhapšen i poslat u koncentracioni logor Terezinštad, gde je umro 1942.
Koristeći papir sa opisanom kvadratnom mrežom, možemo primeniti Pikovu teoremu da procenimo površinu regiona (recimo države), ako njegove granice aproksimiramo pomoću poligona. Naravno, ukoliko je mreža gušća, rezultat će biti tačniji. Na slici 2 poligonom su približno ograničene granice američke savezne države Teksas. U ovom slučaju izbrojali smo U = 101, G = 52, dok je ivica kvadrata mreže oko a = 72 kilometara. Kratka računica daje površinu Teksasa
P = (U + G/2 – 1) x 722 = 126 x 5184=653 184 km2.
Tačna površina je PT=696 240 km2, što znači da je načinjena greška od oko 6,6\%.
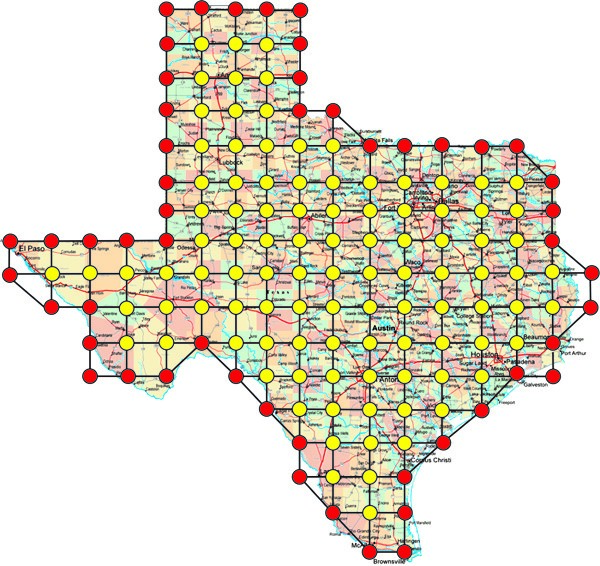
Sl. 2 Izračunavanje površine Teksasa
Pikova teorema može se iskoristiti u rešavanju jednog interesantnog zadatka koji se odnosi na zatvoreni skakačev put. To je zatvoreni nepresecajući put sastavljen od poteza skakača na šahovskoj tabli.Dokazati da je površina okružena zatvorenim skakačevim putem celobrojni umnožak površine jednog kvadrata šahovske table n x n (n > 3).
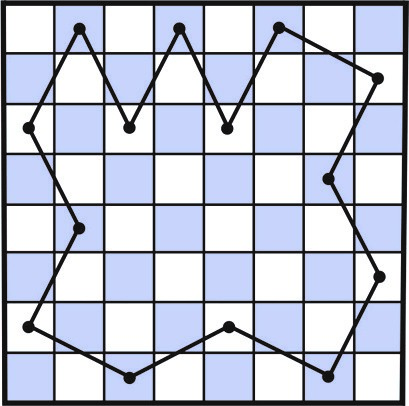
Sl. 3 Površina ograđena zatvorenim skakačevim putem
Rešenje: Neka je S površina kvadrata šahovske table dimenzije n x n.Primenjujući Pikovu formulu A =(U + G/2 – 1) S, dovoljno je pokazati da je U + G/2 – 1ceo broj, a to će biti ako je G paran broj. Pošto se skakačev put sastoji naizmenično od belih (b) i crnih polja (c), u slučaju bilo kog zatvorenog puta (polazno polje je i završno) lako je zapaziti da je broj polja preko kojih je prešao skakač uvek paran. Zaista, niz c (početak) – b – c – b – \cdots – c -b – c (kraj), pridružen zatvorenom skakačevom putu, uvek ima paran broj poteza; videti sliku 3. Kako je broj kvadrata koji pripadaju zatvorenom skakačevom putu jednak broju graničnih tačaka G, dokaz je kompletiran.
Dodajmo još da sa slike 3 nalazimo da je U = 34, G = 14,odakle na osnovu Pikove teoreme sledi da je površina ograničena zatvorenom putanjom skakača u ovom konkretnom primeru jednaka A = 34 + 14/2 – 1 = 40.








