Дакле, можемо рећи да су фермиони снобови и да не воле много да се друже, те стога неће у исто стање, док су бозони темпераменти медитернаци који воле дружење и журке. Некад се питам, ко бисмо били ми Срби у свету честица? То вама остављам на размишљање иако наслућујем одговор.

Данило Николић
- Мноштво је различито – даме и господо професор Гибс
Да бисмо наставили нашу причу започету у првом наставку, а у циљу покушаја да објаснимо лепоту суперпроводности, рећи ћемо пар речи о системима састављеним од мноштва честица. Физичари, како они који се баве њоме на истраживачком нивоу, тако и људи који нису истраживачи али су поклоници природних наука често су склони да под појмом фундаментална физика подразумевају теорије елементарних честица од којих је саздан свет који нас окружује.
Једна од таквих особина јесте и феномен
суперпроводности – колектив честица
који показује нулту отпорност при
„проласку” кроз кристалну решетку.
Међутим, нобеловац Филип Андерсон у свом знаменитом тексту More is different (Science, 1972.) истиче – понашање великих и комплексних скупина елементарних честица, испоставља се, не може бити схваћено као једноствна екстраполација особина неколико честица. Испоставља се да мноштво честица испољава одређене особине умногоме различите од особина које поседују појединачно. Једна од таквих особина јесте и феномен суперпроводности – колектив честица који показује нулту отпорност при „проласку” кроз кристалну решетку. Да бисмо дошли до објашњења овог феномена кренимо са историјом како то увек бива.
У првој половини 19. века пажњу научника почињу да привлаче топлотне појаве. Развојем парне машине и индустријске револуције постало је јасно да је значај топлотних машина веома велики, чиме се на ноге поставља наука о преносу топлоте – термодинамика. Пиониром термодинамике сматра се Никола Карно чији рад је директно био мотивисан повећањем ефикасности топлотних машина што је сматрао основним условом који може обезбедити победу Француске у Наполеоновим ратовима. Како било, Наполеон је поражен на крају.
Временом се схватило да наука о топлоти има одређене универзалне принципе који се не тичу само рада топлотних машина (тзв. топлотни циклуси), тако да термодинамика своје прве дефиниције добија средином 19. века кроз радове лорда Келвина и Рудолфа Клаузијуса, да би свој врхунац доживела кроз статистичку дефиницију Максвела и Болцмана. Сва ова имена су врло добро позната поштоваоцима природних наука.
Међутим, један од главних хероја у нашој данашњој причи јесте један други физичар – Џосаја Вилард Гибс (Josiah Willard Gibbs, 1839-1903.), име можда мање познато од претходно поменутих, а које је заокружило причу започету радовима Максвела и Болцмана. Иако његово име не звучи познато свима, ја ћу вам рећи да је то један од највећих физичара икада. Теоријски концепт који је он развио претрпео је све револуције у науци до данас у мање-више неизмењеној форми – концепт усредњавања што представља централно место статистичког описа природе. Мотивисан радовима поменуте господе Максвела и Болцмана који заснивају статистички опис (класична Максвел-Болцманова статистика), Гибс га математички заокружује 1902. уводећи појам статистичког ансамбла.
Пошто нам намера није да урањамо у компликоване математичке рачуне, покушаћу у пар реченица да објасним појам ансамбла на начин надам се разумљив нашим читаоцима. Размотримо ваздушни притисак. Интуитивно је јасно да је он повезан за број судара честица ваздуха (рецимо да су то све идентични атоми) са зидовима суда. Поставља се питање када меримо притисак неким барометром, шта ми тачно меримо? Да, управу сте, меримо сударе честица и површине сонде нашег инструмента. Питање је који број судара меримо? Да ли детектујемо сваки појединачни судар са сондом?
Не, наш инструмент не може имати ту резолуцију, наш инструмент мери неки средњи број судара у неком временском интервалу. Зато и има потребе и јединог значаја у термодинамици константно говорити о неким средњим вредностима. Међутим, питање је шта ће нам неки ансамбли ту? Једноставно, наше теорије не могу да усредњавају по времену. Системи су и сувише комплексни да бисмо могли све једначине кретања појединачних честица да решимо и да добијемо временску еволуцију система.
Зато велики Гибс нуди алтернативу. Замислимо да имамо систем честица гаса (рецимо ваздуха) одређене запремине и температуре. Претпоставимо да је и енергија гаса фиксирана и нека нас интересује рецимо притисак, односно средњи број судара са границама наше запремине. Шта да радимо кад не знамо временску еволуцију система? Па Гибс нам даје рецепт – усредњи по свим могућим микроскопским реализацијама. Како то мислите, професоре? Па, лепо испитај које све конфигурације честица у твом суду ће задовољити услове задате температуре и енергије у нашем суду. Уједно, ово је и дефиниција статистичког ансамбла.
Мало ћу овде заронити у математику
па ћу вам рећи да једној конфигурацији
одговара једна тачка у фазном простору,
који има 6N димензија, где је N број
честица! Уврнуто, рећи ћете. А ја кажем
– да, уврнуто, али мене више леђа не боле,
што би рекла бака на реклами.
Дакле, статистички ансамбл представља скуп свих копија, свих микроскопских сценарија који ће задовољити макроскопски задате параметре. Дакле, као да заледимо 50 конфигурација честица које ће нам дати ту и ту енергију и температуру. Наравно подразумевамо и да је број честица задат. Мало ћу овде заронити у математику па ћу вам рећи да једној конфигурацији одговара једна тачка у фазном простору, који има 6N димензија, где је N број честица! Уврнуто, рећи ћете. А ја кажем – да, уврнуто, али мене више леђа не боле, што би рекла бака на реклами. Напоменуо бих само да енергија не мора бити фиксирана, као ни број честица. Али не бих више о овоме дебатовао, јер све даље би нас бацало у математички опис, што није циљ на овом месту.

Слика 1. Максвел-Болцманова расподела честица по брзинама за различите гасове (лево) и Џозаја Вилард Гибс (десно) (преузето са Википедије)
- Квантне компликације – наступа Паули
Као што смо видели у првом делу смо се бавили класичним гасом. И ствари су већ почеле да делују компликовано (морамо да мислимо у 6N димензија). Међутим, ми смо авантуристи и не волимо једноставне ствари, тако да живот може бити још компликованији. Да, квантне компликације су оно што желимо.
Подсетимо се на тренутак да у квантној механици централно место заузима таласно-честични дуализам. Дакле, честице се на неки магични начин некада понашају као таласи одређених таласних дужина. Када су високе температуре честице су срећне и врло раздрагане, тако да можемо рећи да су добро локализоване и на плесном подијуму растојања су велика, односно да их можемо сматрати куглицама. Међутим, снижавањем температуре њима се спава, тако да се полако „гурају” једна до друге до тренутка када су растојања међу њима у просеку упоредива с таласним дужинама додељених таласа и тада долази до омиљене појаве многих физичара с магичним именом – интерференција.
Централно место наше приче у овом
одељку заузима можда и најважнији
принцип природе, за који немамо
објашњење поред тога да има универзалну
важност – Паулијев принцип искључења.
Условно речено, таласне функције се преклапају испољавајући нове – квантне особине. Дакле, можемо очекивати на ниским температурама испољавање драстично дручачијих особина гасова него на собној температури, а то са собом вуче и нову физику, физику квантних статистика.
Централно место наше приче у овом одељку заузима можда и најважнији принцип природе, за који немамо објашњење поред тога да има универзалну важност – Паулијев принцип искључења. Као што знамо сваки електрон има своју масу, наелектрисање, али и нешто што се зове спин. Ако бих на било који начин покушао да га осликам погрешио бих. Уобичајено је да се он замишља као ротација електрона око своје осе, што је мало бесмислено уколико разумемо да електрон није куглица.
Зато ћу ја рећи да је спин фундаментална карактеристика честица као што је рецимо наелектрисање. Спин електрона може имати две вредности (тзв. пројекције спина) , где је потоњи знак тзв. Плакнова константа (или прецизније редукована Планкова константа). И то важи за све електроне у универзуму. Међутим, електрони нису једине честице у природи. Постоје честице и са другим избором ових пројекција и то нас води једној универзалној подели – честице са полуцелобројном пројекцијом спина зване фермиони, док су њихови другари са целобројним спином ( ) познати у друштву честица као бозони. Али какве то везе има са Паулијем, тим симпатичним буцом из Аустрије?
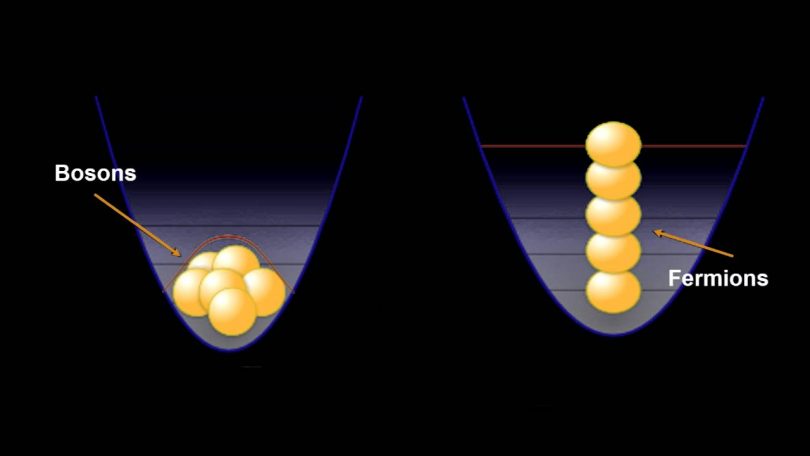
Као што знамо честице могу имати различите енергије. Свакој од тих енергија у квантној механици одговара једно стање (некада и више, али ради једноставности претпоставимо да је само једно). Дакле, талас може имати различите форме, са различитом енергијом. Паули каже следеће – само две (или више) честице са целобројним спином се могу налазити у истом квантном стању, док је за оне друге то строго забрањено. Дакле, можемо то рећи у маниру да су фермиони снобови и да не воле много да се друже, те стога неће у исто стање, док су бозони темпераменти медитернаци који воле дружење и журке. Некад се питам, ко бисмо били ми Срби у свету честица? То вама остављам на размишљање иако наслућујем одговор.
Веровали или не, као што рекох овај једноставан принцип је можда најважнији и најуниверзалнији принцип природе! Али какве то везе има с нашом почетном причом? И те како има. Из горњег исказа видимо да квантна стања се не попуњавају увек на истоветан начин, односно горепоменута интерференција није идентична за фермионе и бозоне, што се фундаментално одражава у чињеници да Максвел-Болцманова статистика која важи за класичне гасове, није више на снази и бива замњена двема новим тзв. квантним статистикама – Ферми-Дираковом (па отуда фермиони) и Бозе-Ајнштајновом (бозони). Ове статистике се разликују само за један минус, али последице су фантастичне! А какве то везе има са нашом причом о суперповодности видећемо у следећем и последњем делу наше приче.

Слика 2 Волфганг Паули (лево) и Нилс Бор (десно) се играју кинеском чигром (tippе top). Стиче се утисак да велики умови остају деца током целог свог живота (преузето са Cosmolearning.org)





Бајковито, маштовито и мени сликовито,
Цитат:
„Теоретичари постижу своје врхунске животне домете најчешће у младости; код њих креативни сокови крену рано, а почну да пресушују већ са петнаест година – тако се, барем, чини. Потребно је да теоретичар има само онолико знања колико му је потребно, и не више од тога; док је млад, још није погурен под теретом сувишног интелектуалног пртљага који се временом нагомилава“.
Сведочи – ЛИОН ЛЕДЕРМЕН
Veoma inspirativan i intrigantan tekst. Veoma se retko u naučnim raspravama sa ozbiljnom tematikom može videti ovako duhovit i koncizan pristup. želeo bih da se u sledećem nastavku baci akcenat na postizanje superprovodnosti na višim temperaturama što bi imalo dalekosežne benefite na zemlji kao i moguće futurističke projekte u kosmosu s obzirom na temperature koje tamo vladaju.