Решења за ових шест задатака су, по правилу, кратка и налазе се на крају чланка.

Проф. др Миодраг Петковић
Подела наследства. Тројица браће треба да поделе крдо од 17 коња, које им је оставио отац у наследство, тако да најстарији брат добије 1/2 свих коња, средњи 1/3, а најмлађи 1/9. С обзиром да је 17 прост број и није дељив ни са једним од бројева 2, 3, 9, браћа су се досетила и позајмила од суседа једног коња и решила проблем на описани начин. Да ли је баш све у реду?
Планински пут. Једног дана, тачно у 6 ујутру, љубитељ природе кренуо је аутомобилом уз планину уским путем који је спирално водио до планинарског дома близу врха. Возач је ишао неравномерном брзином, често се одмарајући на свом путу да би разгледао прелепу околину или појео сендвич. На врх планине стигао је пред залазак сунца. Пошто је преспавао у планинарском дому, сутрадан ујутру у 6 сати кренуо аје утом низ планину. Спуштао се истим кривудавим путем, мада брже него него при пењању, повремено се одмарајући да би јео или фотографисао поједине пределе. Доказати да постоји тачка на путу у коју ће он доспети приликом вожње низбрдо тачно у исто време као и претходног дана док се возио уз планину.
Изгубљени долар. За заједнички ручак у кафани три госта г1, г2, и г3 платила су келнеру K по 5 долара. Благајник Б за касом рекао је келнеру да ручак укупно кошта 10 долара и дао је келнеру 5 долара назад да их проследи гостима (видети слику 1). Kелнер је сваком госту вратио по један долар и за себе задржао два долара. Дакле, сваког госта ручак је коштао по 4 долара, што укупно износи 12 долара, и ако се додају 2 долара које је келнер задржао за себе, то укупно износи 14 долара. Где се изгубио један долар?
Гужва у авиону. 300 путника се укрцава у авион који има 300 седишта. Путник који је први ушао изгубио је своју картицу с бројем седишта и бира седиште насумице. Сваки следећи путник седа на своје место, ако није заузето, у противном, и он насумице бира где ће да седне. Kолика је вероватноћа да последњи, тристоти путник, седне на своје место?

(Wikipedia)
Носачи авиона на полусфери. Три носача авиона A, B и C патролирају морима и океанима света. Колика је вероватноћа да се ова три брода нађу у истој хемисфери (полулопти) у неком погодном тренутку?
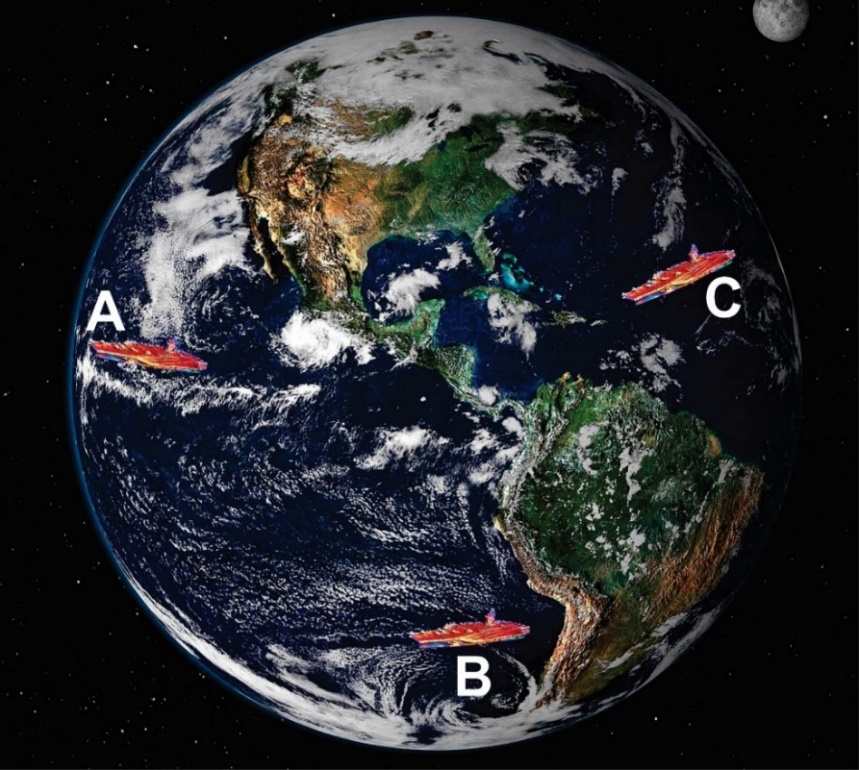
(Wikimedia Commons)
Планетарни тунел. Kопнени део једне планете у сунчевом систему Алдебаран састоји се од великог броја острва чија укупна површина (копнени део) заузима нешто више од половине површине планете. Доказати да становници ове планете могу ископати праволинијски тунел кроз центар планете, почињући и завршавајући свој тунел на копну. Претпоставља се да је њихова технологија довољно развијена за овај подухват.

(Pixabay)
Решења
Подела наследства: Подела није извршена правилно, нити је то могуће учинити. Наиме, како је 1/2+1/3+1/9=17/18, дакле, мање од 1, при подели било којег броја коња јавио би се остатак. Због тога је подела према тестаменту немогућа, упркос сналажљивости браће. Да је у тестаменту писало да подела треба да се изврши у односу 2:6:9, први син би добио 9 коња, други 6, а трећи 2 (као на слици 1), што би у збиру заиста дало број 17.

Сл. 1 Подела наследства – манипулације са коњима
Планински пут: До решења се долази коришћењем врло једноставне али ефектне идеје. Претпоставимо да у вожњи планинским путем учествују два возача: возач А који је у 6 часова ујутру почео да се пење уз планину да би дошао до планинарског дома, и возач B који је у исто време истог дана истим путем почео да се од планинарског дома спушта низ планину. У неком моменту, рецимо у 11 сати, они се морају срести на путу; тачка сусрета X је управо тражена тачка јер је од времена поласка обојице возача протекло исто време – пет сати.
 Редизајн слике Морица Волфа (предео у Норвешкој)
Редизајн слике Морица Волфа (предео у Норвешкој)
Изгубљени долар: Долар није изгубљен; 2 долара која је узео келнер K не треба додавати износу од 12 долара већ одузети од овог износа да би се дошло до 10 долара, колико износи рачун. Ситуација је веома јасна: код благајника Б је остало 10 долара (износ рачуна), 2 долара код келнера K и по 1 долар код гостију Г, што износи тачно 15 долара.
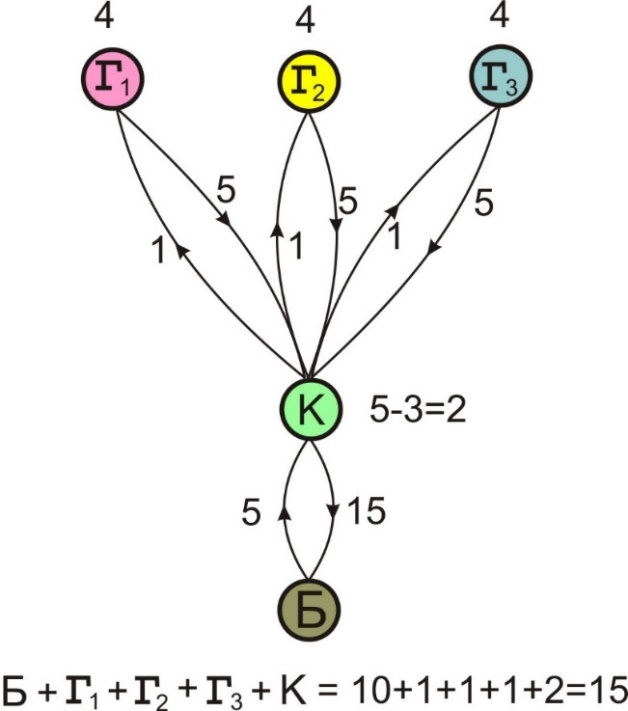
Граф изгубљеног долара
Гужва у авиону: Kада тристоти путник уђе у авион, последње слободно место мора бити оно што је додељено првом путнику (који је изгубио број седишта) или намењено последњем путнику. Оба догађаја су једнако вероватна, тако да је шанса да последњи путник седне на своје место 50%.
Носачи авиона на полусфери: У сваком тренутку три носача авиона се налазе на истој полусфери. У ово се можемо лако уверити ако кроз две произвољне тачке, рецимо А и B, и центар сфере поставимо раван. (Kао што је познато, три неподударне и неколинеарне тачке у простору увек одређују раван). Видети слику 2 где зелено обојен круг представља пресек равни и сфере. На тај начин сфера ће бити пресечена на две полусфере – трећа тачка C припадаће једној од њих.
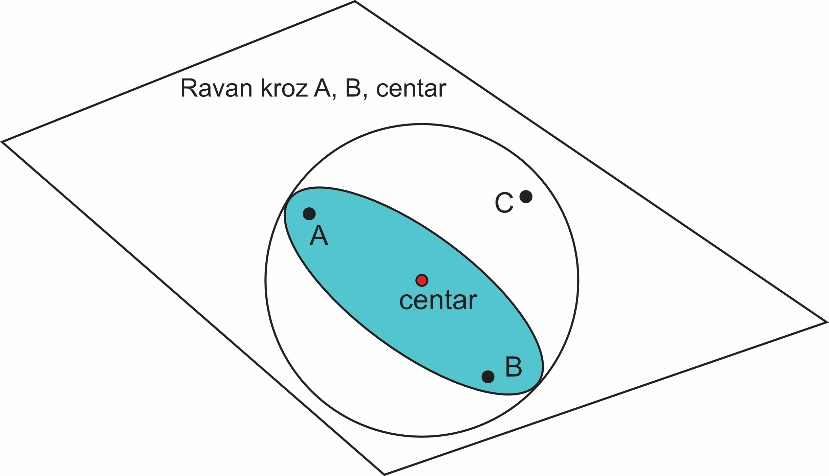
Сл. 2 Три носача авиона на истој хемисфери
Планетарни тунел: У решавању овог задатка користићемо следећи једноставан и интуитивно јасан али врло користан Дирихлеов принцип (Johan Gustav Dirichlet, 1805-1859):
Ако ставимо М+k објеката у М кутија, тада бар једна од кутија мора да садржи два или више објеката.
На пример, ако у 10 кутија ставите 13 лопти, тада ће се у бар једној кутији наћи бар две лопте.
Ево сада решења постављеног проблема о планетарном тунелу. Замислимо да су сви делови копна обојени црвеном бојом. Ако у односу на неки (црвено обојен) копнени део А постоји дијаметрално супротан копнени део B, поред црвене боје додајмо овом делу и зелену боју. С обзиром да копнени део заузима више од половине површине планете, на основу Дирихлеовог принципа мора постојати бар једна тачка B која је обојена обема бојама. Kопање тунела треба започети у тачки B, а завршиће се на копненом делу у тачки А.
(Илустрација Тријумфална Pi-капија/фото и редизајн В. Петковић)






