БРОЈ π У ДОБА РАЧУНАРА

Средином двадесетог века наступила је ера електронских рачунара тако да је романтична трка за рекордом у израчунавању броја π била практично завршена. Већ 1949, користећи развој аркус тангенса, тим који су предводили Џорџ Рајтвизнер и Џон фон Нојман, достигао је 2.037 децимала броја π на рачунару ENIAC. Једна од Ојлерових формула за аркус тангенс је омогућила Жану Гулоу и Мартину Бујеу да 1973. израчунају милион децимала броја π, браћа Чудновски су 1989. сопственом формулом први пребацили милијарду итд.

Проф. др Миодраг Петковић

 

У штампаној верзији Нове Галаксије (број 1/2024) професор Милан Д. Тасић дао је изузетно едукативан и систематичан кратак преглед историје математичких константи, концентришући се највише на константе

а и на неке природне бројеве са интересантним својствима. Зашто влада толико интересовање за број π? Пошто је π блиско повезан с кругом, налази се у многим формулама из геометрије и тригонометрије, посебно у онима које се тичу круга, сфере или елипсе. Друге гране науке, као што су вероватноћа, статистика, физика, Фуријеова анализа, теорија потенцијала, теорија бројева, Хајзенбергов принцип неодређености и тако даље, такође укључују π у неке од својих важних формула.

Разматраћемо неке особине и формуле за израчунавање најпознатије математичке константе π до којих се дошло искључиво помоћу електронских рачунара негде од средине 20. века па надаље. Енглески математичар-аматер Вилијам Шенкс је 1853. године израчунао 530 децимала (527 тачних) броја π (Contribution to Mathematics, Лондон 1853, стр. 86-87). Он је двадесет година касније, помоћу механичког калкулатора, израчунао 707 децимала. На његову жалост, грешка у 528. децимали из 1853. проузроковала је да свих 180 последњих цифара буде погрешно. То је 92 године касније утврдио Данијел Фергусон (Nature, March 1946, с. 342) помоћу механичког стоног калкулатора.

Сто година после Шенкса наступила је ера електронских рачунара тако да је романтична трка за рекордом у броју тачних цифара броја π била практично завршена. Иронично и помало трагично делује вишегодишња опседнутост неких истраживача (Лудолфа ван Цојлена и Шенкса пре свих) децималама броја π. Данас се помоћу ефикасних алгоритама и моћних рачунара готово свакодневно израчунају билиони децимала и већ је тешко пратити рекорде. Присетите се да се у укрштеним речима број π појављује под називом Лудолфов број – Лудолф је значајан део свог живота провео израчунавајући вредност броја π. До краја живота, 1610. године, израчунао је број π на 35 тачних децимал које су урезане на његовом споменику у Лајдену.

При крају двадесетог века браћа Дејвид и Грегори Чудновски објавили су следећу формулу за рачунање броја π

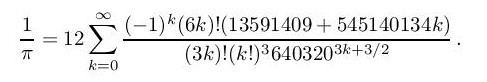
Користећи ову формулу они су 1989. године поставили светски рекорд у израчунавању броја π са 480.000.000 децималних места. У следећих пет година још четири пута су постављали светски рекорд. Браћа Чудновски су добила инспирацију за своју формулу анализирајући ред

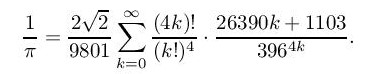
чувеног индијског математичара Сринивасе Рамануџана. Мада веома ефикасна, формула браће Чудновски је помало бледа у поређењу са сензационалним резултатом  истраживача Дејвида Бејлија, Питера Борвина и Сајмона Плуфа. Они су 1996. открили нову формулу за израчунавање цифара броја π (познату као ББП-алгоритам):

 

По чему је формула (1) тако фасцинантна? Она омогућава да израчуна специфична цифра броја π без израчунавања претходних цифара. Једина мала препрека је да оне нису децималне цифре већ хексадецималне (основа 16), од којих се могу добити цифре у базама 8, 4 или 2, а затим их конвертовати у децималну базу. Већ следеће године познати француски математичар и програмер Фабрис Белар је користећи ову формулу показао да је стомилијардита хексадецимална цифра броја π једнака 9. Тренутни рекорд је постигнут управо на π-дан 2024 (тј. 3/14/2024, на основу форме записа датума у неким државама или регионима), а остварили су га Џордан Ранус, Кевин О’Брајен и Брајан Билер. Рекорд износи 105 билиона децималних цифара, број који се пише са 15 децималних цифара (извор: Википедија).

НАПОМЕНА 1. Да би се избегла могућа конфузија, број са 9 нула после 1 у САД и Британији се назива билион, трилион је број са 12 нула после 1 итд. Међутим, у неким земљама билион је еквивалентан са милијардом (нпр. у Србији, на шпанском је милардо, на француском, пољском и руском милиард, на немачком милиарде). Затим, следи наш билион (англосаксонски трилион), па наш трилион, дакле, нека врста транслације за 10³ (10^3).

НАПОМЕНА 2. За израчунавање броја π на огроман број децимала и верификацију резултата потребан је суперкомпјутер велике меморије (реда терабајта) и изузетне брзине извршавања операција (реда 10¹⁵ (10^15) у секунди или више), мада има и изузетака у случају алгоритма ББП-типа који је усавршио Фабрис Белар – он је користио гејмерски персонални рачунар од 3.000 долара. У последњој деценији математичари и програмери су неке рекорде постигли користећи Google Cloud платформу; то је заправо огромна мрежа рачунара (локација и број рачунара је строга тајна).

Сврха израчунавања броја π и нове трке за рекордима је, углавном, тестирање нових компјутерских система, пре свега компјутерске аритметике. Израчунавање броја π је нека врста теста на стрес за компјутере, врста „дигиталног кардиограма”, наводе неки експерти за компјутерске науке. Осим тога, ова израчунавања су важна у креирању   брзих алгоритама за извршавање основних аритметичких операција, специјално у аритметикама с вишеструком прецизношћу, а и за генерисање (псеудо)случајних бројева. Наравно, неки програмери и математичари раде оваква израчунавања да би дошли до зрнца славе у случају да поставе рекорд и обезбеде мали простор у новинама.

У наставку неколико интересантних и необичних чињеница и особина које се односе на број π.

• Математичари и компјутерски стручњаци се годинама питају да ли је низ цифара броја π статистички случајан низ, тј. да ли се цифре од 0 до 9 јављају без периода и у просеку од 10% свака. Провера на првих неколико милијарди (билиона, што би рекли Американци и Британци) децималних места показала је да је поменути низ највероватније статистички случајан низ. Управо је овај приступ помогао поменутом Данијелу Фергусону да наслути грешку у Шенксовом израчунавању броја π на 707 децимала (1873) јер се цифра 7 појављила приметно мање у резултату него остале цифре.
• Често се поставља питање појаве одређеног низа цифара у развоју броја π, на пример, низа 314159 првих шест цифара броја π. Овај низ се јавља шест пута међу првих 10 милиона цифара у децималном развоју броја π. С друге стране, низови 00000000 и 123456789 се не јављају у развоју од неколико милијарди цифара, али то не значи да их сигурно нема; у ствари, ово је питање које припада групи математичких проблема на које се не може одговорити, не само у овом тренутку већ можда никад. Али, да је све могуће казује следећи пример: све децимале броја π почев од 762. до 767. (укупно шест) су деветке, а да почев са 710.150. децималом следи седам узастопних тројки: …3537333333386… Ово је заиста чудесна особина коју је приметио Доналд Кнут, професор рачунарских наука са Стенфордског универзитета и добитник престижне Тјурингове награде, захтевајући од својих студената да израчунају број π са 15 милиона децимала користећи тада актуелну формулу Е. Саламина. Иначе, поменута 762. цифра (од које стартују деветке) популарно се назива Фајнманово место по презимену чувеног америчког физичара и нобеловца Ричарда Фајнмана, који се једном кладио да ће научити напамет децимални развој броја π до децимале од које почиње низ 999999. Не зна се да ли је то и урадио, бар аутору овог прилога није познато.
• Постоје различите технике за памћење цифара броја π на различитим језицима а састоје се углавном од духовитих реченица. Једна од најпознатијих на енглеском језику (аутор је чувени писац научне фантастике Исак Асимов) јесте следећа: How I want a drink, alcoholic of course, after the heavy lectures involving quantum mechanics.(Kako želim piće, alkoholno naravno, posle teških predavanja koja uključuju kvantnu mehaniku).

Број слова сваке енглеске речи у овој реченици представља вредност цифре у апроксимацији 3,14159265358979 – 14 тачних цифара.

Ево још једне памтилице: May I have a large container of coffee? (Mogu li dobiti veliku šolju kafe?)

И једне на српском језику:

Сл. 1 π-памтилица

• Позната британска певачица Кејт Буш (Wuthering Heights, Babooshka, Running Up That Hill, Cloudbusting…) је на свом албуму Aerial (2005) опевала број π: Sweet and gentle and sensitive man, With an obsessive nature  and deep fascination for numbers, And a complete infatuation with the calculation of number pi. У преводу: Драг и нежан и осетљив човек, Пун страсти, дубоко фасциниран бројевима, И потпуно посвећен рачунању броја пи. Њему (том драгом и нежном човеку) у част Кејт Буш у наставку песме набраја првих 120 децималних места броја π. Нажалост, уз грешке и пропусте, али зар је то важно када се ради о песми.
• Број децимала броја π упамћен помоћу разних реченица и стихова делује готово смешно у поређењу с бројем цифара које је запамтио Акира Харагучи, пензионисани јапански инжењер. Он је изрецитовао 100.000 децималних цифара броја π за 16 сати, од 3. октобра до 4. октобра 2006. С обзиром да Guinness World Records још није признао овај рекорд (према мом сазнању), на снази је рекорд од 67.890 цифара које је изрецитовао Кинез Лу Чао за 24 сата 20. новембра 2005.
• У САД и Великој Британији се 14. март (који се записује као 3/14) слави као π – дан. Алберт Ајнштајн се родио на π-дан 1879. у Улму, Немачка. Управо на π-дан 2024. постављен је нови светски рекорд у броју децимала броја π, што је наведено у уводном делу.Број

• Број

је веома близак броју 20.

• Још невероватнији је резултат

у којем после осамнестоцифреног броја иза децималне запете следи 12 деветки. Чувени индијски математичар Сриниваса Рамануџан је знао да овај број није цео, али је претпоставку да би ово могао да буде цео број објавио у априлском броју часописа Quarterly Journal of Pure and Applied Mathematics (Vol. 45, 1913-14) као првоаприлску шалу у договору са уредником часописа.

• 1998. године снимљен је филм Пи (режисер Дарен Ароновски) о математичару који почиње да луди трагајући за узорком у развоју броја π којим би постигао успех на берзи и добио одговоре на нека питања о универзуму. Број π се такође јавља у Хичкоковом филму Torn Curtain (1966) и филму The Net (режисер Ирвајн Винклер, 1995) у којем главну улогу игра Сандра Булок.
• У епизоди Wolf in the Fold чувене ТВ серије Звездане стазе, капетан Спок зауставља полудели рачунар наредбом: „Израчунај последњу цифру броја π”, чиме га наравно збуњује и спречава да даље чини лоша дела. Сетите се филма War Game (1983) у којем је војни суперкомпјутер WORP скоро започео нуклеарни рат, али га је млади хакер (Метју Бродерик) надмудрио задавши му задатак да игра познату игру тик-так-тое (или X-О) против себе самог. Ова игра нема победника ако се игра правилно и суперкомпјутер прекида лансирање ракета јер из претходне игре закључује да ни евентуални нуклеарни рат нема победника.

• Једно трик-питање: Колика је запремина пице (pizza) дебљине а и полупречника z? Одговор:

• Чувена модна кућа Givenchy лансирала је парфем за мушкарце под називом π, рекламирајући да је намењен интелигентним и визионарски настројеним мушкарцима.
• Године 2012. у Њујорку, у 26. улици на Менхетн скверу, отворен је јединствени Музеј математике МоМат (видети слику 2 – улаз у Музеј). Поред многих занимљивих експоната, у продавници сувенира могу се купити и позлаћене минђуше у облику слова π (слика у углу). Ако вам се овај сувенирчић не свиђа, одмах преко пута музеја имате пеглу – чувену зграду Флетајрон (Flatiron, пегла) у облику пегле (дели их Пета авенија), први њујоршки облакодер и једна од најпопуларнијих зграда у САД према анкети из 2023. Још је актуелна (мада непоуздана) прича да је у овој згради радио као лифтбој чувени филмски глумац Кери Грант пре него што је постао познат.

На крају ево једне приче о великом достигнућу из 18. века о којем моја, а и данашње генерације. не би ни хтеле да размишљају без рачунара. А питање је да ли би многима рачунар уопште нешто и помогао. Пјетро Менголи (1626-1686), италијански свештеник и математичар, професор математике на универзитету у Болоњи, највише је познат по изучавању бесконачних редова. Године 1644.  поставио је питање да ли је сума свих реципрочних вредности квадрата природних бројева

коначан или бесконачан број. Овим питањем највише су се бавили чланови математичке породице Бернули и Леонард Ојлер, сви из Базела (Швајцарска), тако да је задатак постао познат као Базелски проблем. После десетогодишњег рада Ојлер је 1735. дао одговор који гласи:

дакле, сума је коначан број и дата је изразом на десној страни. Многи математичари сматрају ову формулу једном од најлепших у математици. Данас се горња сума може наћи на више начина (на пример, помоћу интеграције погодног бесконачног реда или помоћу тригонометријских редова).

Поставља се питање како је Ојлер израчунао суму реципрочних вредности квадрата природних бројева? До резултата је дошао мукотрпним десетогодишњим радом простим рачунањем или методом оловка-и-папир. Најпре је израчунавањем једног интеграла добио резултат 1.644934 са шест децимала, а у другом кораку повећао је тачност суме на 17 децимала! Мора се признати да је то био невероватан подвиг без калкулатора или рачунара, али треба поменути и чињеницу да је славни математичар имао изузетну меморију. Ево једног поређења: 16-битни рачунари произведени средином шездесетих година двадесетог века (на пример ИБМ 1130 – пола дванаест, први рачунар на којем сам као студент радио), могли су да дају резултате тачности до 10 значајних декадних цифара.

У другом кораку Ојлер је препознао да резултат износи

После овог нагађања, било је потребно да заиста докаже претпостављени резултат, што му је одузело више година рада. Као што је било уобичајено у то време, Ојлер је више година држао у тајности да зна резултат (то су чинили понекад Њутн и Гаус), чиме је обезбедио предност над конкурентима. Чување изузетних резултата није било ретко у 16, 17 и у 18. веку јер су чувари тајни тако могли да добију позицију на универзитету пре других или освоје неку престижну награду.

НАПОМЕНА 3. У литератури се може наћи и опис Ојлеровог доказа у којем је коришћен развој функције sin x/x и њеног трансформисања у бесконачан производ, касније познат као Вајерштрасова факторизациона теорема.

(Илустрација В. Петковић, П. Капус)