Неки практични проблеми, код којих на први поглед недостају сви подаци, могу се решити користећи елементарно познавање математике наравно уколико се пронађе права идеја. У овом прилогу тражи се локација закопаног блага која зависи од положаја еукалиптуса, палме и вешала на пустом острву које су некад користили гусари. Међутим, после два или три века вешала су иструлела, дакле, нема довољно података! Kористећи само средњошколско познавање елементарне геометрије, показује се да је место где је закопано благо ипак могуће пронаћи. Импресивно, едукативно, једноставно. Вешала су иструлела, али је овај задатак преживео бар два века, из генерације у генерацију.

Проф. др Миодраг Петковић
Руско-амерички теоријски физичар и космолог Џорџ Гамов (1904-1968) познат је по томе што је први детаљно разрадио теорију о Великом праску засновану на идеји белгијског свештеника, математичара и астронома Жоржа Леметра. Последњих година живота бавио се популаризацијом науке. У својој књизи One, Two, Three… to Infinity, први пут публикованој 1947. године (код нас је књигу издала Техничка књига, Београд 1955, под насловом Један, два, три… до бесконачности), Гамов је изложио више од 120 врло интересантних прилога, почев од математике, физике, биологије, па све до микрокосмоса, макрокосмоса и кристалографије.


Не мали број математичара, физичара и космолога (нпр. Нил Деграс Тајсон) одабрали су своја занимања инспирисани управо овом књигом. За свој рад на популаризацији науке Џорџ Гамов је 1956. добио престижну награду Унескоа. Још као средњошколцу, књига (српско издање) се и мени јако допала и уз мало напора успео сам касније да дођем до издања на енглеском језику. Гамов је дело посветио свом сину речима To my son Igor who wanted to be a cowboy. Поред осталог, Гамов је у овој књизи дао лепу демонстрацију коришћења комплексних бројева у равни и операција са њима у фиктивној причи о острву с благом која следи.
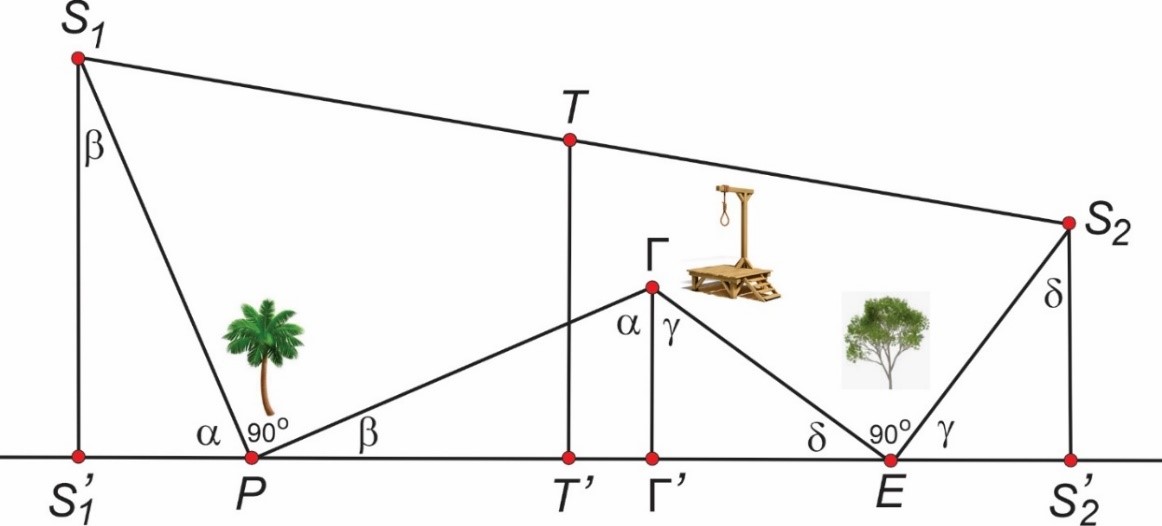
Прича се да је неки морнар нашао стари пергамент који описује тачну локацију пустог осртва са закопаним гусарском благом. Наведене су следеће инструкције за налажење: На острву су вешала и два дрвета, палма и еукалиптус. Пођи од вешала и број кораке у правој линији до еукалиптуса. Kод дрвета скрени за 90 степени налево и ходај напред у правој линији исти број корака. У тачки где станеш забоди штап у земљу. Сада се врати до вешала и ходај у правој линији, бројећи кораке од вешала до палме. Kада стигнеш до палме, окрени за 90 степени надесно и иди исти број корака, стављајући други штап у тачку где се зауставиш. Kопај у тачки тачно на половини растојања између штапова и наћи ћеш благо (сл. 1).
Морнар је одлучио да потражи благо, продао је кућу да набави Харисонов хронометар за навигацију, изнајмио бродић од пријатеља и кренуо на неизвесно путовање. Пријатељ га је испратио тужним нема-шансе-да-се-врати погледом, бацио качкет у море за срећу и забринут отишао у најближу крчму да утопи тугу, али то није битно за ову причу. Морнар је пловио седам дана и седам ноћи, шибали су га ветрови и квасиле олујне кише, пржило сунце, гониле беле ајкуле и морски крокодили, заобишао је у великом луку огромног кита налик Мелвиновом Моби Дику. На крају је, захваљујући Харисоновом хронометру, стигао на пусто острво.
После краћег лутања нашао је палму и еукалиптус. Нажалост, зуб времена је учинио своје, и вешала су иструлела и нестала, а време је избрисало све трагове могуће локације. Не знајући положај вешала, морнар није видео начин на који би нашао блага. После неколико узалудних копања, уз крик разочарања који је, брајсоновски речено, подсећао на крик Тарзана кад промаши лијану, одустао је од копања и вратио се на бродић којим је отпловио кући празних руку (Бил Брајсон, чувени путописац). Једина утеха било му је лишће еукалиптуса за које је чуо да се од њега може направити егзотично уље, те га упаковао у неколико џакова и понео са собом.
Гамов је у поменутој књизи дао елегантно решење користећи комплексне бројеве где је (непознати) положај вешала означио произвољним комплексним бројем. За оне читаоце који се никад нису срели са комплексним бројевима или су једноставно заборавили шта то беше, у овом прилогу дајемо једноставно решење користећи основне елементе средњошколске геометрије, као што је приказано у књизи Ingenious Mathematical Problems and Methods (Dover Publ., 1959), чувеног математичара Роналда Грахама (1935-2020). Kад је већ реч о Грахаму, неизоставно је поменути да је он био један од водећих светских експерата у дискретној геометрији и Ремзијевој теорији, радећи најпре као истраживач у Беловим лабораторијама, а касније као профессор на Kалифорнијском универзитету у Сан Дијегу. Он је познат и по највећем броју икада коришћеном у неком математичком доказу (Грахамов број), управо у Ремзијевој теорији. Тај број је толико велики да се у декадном систему не може представити у познатој васиони, чак и ако се свака цифра представља Планковом мером која износи око 10-38 милиметра.

Роналд Грахам (Wikipedia)
Роналд Грахам је био члан Америчке академије наука и добитник великог броја значајних награда. Познат је и као изванредан жонглер. Можете замислити задовољство студената када је нека од својих предавања почињао жонглирањем са 7 или 8 лоптица. У једном делу кабинета имао је и трамбулину коју је користио за релаксацију у паузама између часова или научног рада. Можда је ово последњи тренутак да га оставимо и вратимо се на његово решење задатка о локацији блага на острву.
Означимо са P и E палму и еукалиптус, а вершала, природно, са Г. Даљем нека су S1′, S2′, T’ и Г’ нормалне пројекције (у односу на праву кроз P и E) тачака које представљају позиције штапова S1 и S2, блага T и вешала Г (видети слику 1).
Сл. 1 Острво с благом – геометријско решење
У наставку ћемо дужину дужи AB, рецимо, означавати са |AB |. На основу услова задатка, имамо
![]()
С обзиром на ове две једнакости и узимајући у обзир да су парови углова
(α, β) и (γ, δ)
комплементарни, то јест,
![]()
налазимо
![]()
Помоћу ових релација и чињенице да је T средина дужи S1S2, добијамо
![]()
и
![]()
Из последње релације налазимо
![]()
Према томе, тачка T’ налази се на половини дужи повучене од палме до еукалиптуса. На основу овог и (1) долазимо до локације блага (тачка Т, енгл. treasure): Одредимо, најпре, средину дужи PE (тачка Т’). Пођимо од P према E праволинијски до средине дужи PE, скренимо улево и пређимо растојање једнако половини дужине | PE| идући нормално на праву кроз P и E. На тај начин долазимо до тачке Т где је закопано благо.
Постоји урбана легенда по којој морнар баш и није остао празних руку. По повратку је започео трговину еукалиптусовим уљем (ако се сећате, понео је са острва доста еукалиптусовог лишћа) и тако се полако богатио. Његови наследници су проширили обим делатности, основали све веће и богатије компаније и, на крају, један од њих је саградио велелепан хотел с коцкарницом у Лас Вегасу. У знак сећања на свог претка – ловца на благо, назвао га је Treasure Island (Острво с благом).

Хотел Treasure Island у Лас Вегасу (М. Петковић)
(Илустрација Еукалиптус и палма/Youtube)






