Божански алгоритам (God’s algorithm) је појам који је настао у дискусији о оптималном решењу Рубикове коцке, али се може применити и на друге задатке или игре комбинаторног типа. Односи се на алгоритам који, следећи правила игре, даје решење у најмањем броју сукцесивних потеза који се не може смањити. Овај број зове се Божански број (God’s number) и његово налажење је изазован али по правилу врло тежак проблем који најчешће захтева примену компјутера, а поред тога често и више година рада.

Проф др Миодраг Петковић
Аутор овог прилога се са великом носталгијом сећа старе ГАЛАКСИЈЕ. Тада није било интернета и овај месечник је у правом смислу био прозор у свет науке. Комплет свих бројева је једна од најдрагоценијих збирки у мојој библиотеци. Осамдесетих година прошлог века са мојим колегом са Електронског факултета у Нишу Љубишом Коцићем пар година уређивао сам рубрику под називом Између игре и математике, која је за циљ имала популаризацију математике. Од многобројних прилога у сећању ми је највише остао један задатак постављен пре више од 100 година а који сам поставио читаоцимаГАЛАКСИЈЕ. Пре него што објасним разлог за овај неизбрисив утисак, сматрам да је потребно објаснити појам Божанског бројакоји се помиње у наслову прилога.
Божански алгоритам (God’s algorithm) је појам који је настао у дискусији о оптималном решењу Рубикове коцке (коју ћемо поменути у другом делу овог прилога), али се може применити и на друге задатке или игре комбинаторног типа. Односи се на алгоритам који, следећи правила игре, даје решење у најмањем броју сукцесивних потеза који се не може смањити. Овај број зове се Божански број (God’s number) и његово налажење је изазован али по правилу врло тежак проблем који најчешће захтева примену компјутера, а поред тога често и више година рада. Понекад се овај појам употребљава за максималан број потеза уколико је циљ игре /задатка остваривање максималног броја потеза (видети пример 3).
Треба нагласити да проблеми представљени у овом прилогу и њима слични нису ни неважни нити су само забава и губљење времена, како неки научници желе то да представе. Да је то случај, тада би било без икаквог значаја и израчунавање броја π више од 100 децимала (број довољан за било каква израчунавања у познатом универзуму), чувени проблем четири боје, слично је и са Кеплеровим проблемом о најгушћем паковању сфера, компјутерским програмима за играње шаха и других игара, итд. Ипак, научници широм света, пре свега математичари и програмери, су веома посвећени овим проблемима и раде на њиховом решавању и више година. Разлог је једноставан:процес решавања који захтева нове алгоритме, нове теорије и нове технике веома је користан у области вештачке интелигенције, за тестирање софтвера и хардвера рачунара и још много тога.
А ево и текста поменутог задатка.
У време председничких избора у САД 1908. године велики успех код публике имала је загонетка-играчка приказана на слици.
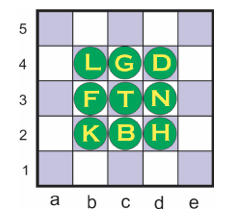
Свака фигура на плочи 5 x5 представља председничког кандидата: L– Лафолет, G– Греј, D– Џонсон, F– Фербанкс, Т – Тафт, N– Нокс, К – Кенон, B– Брајен, H– Хогс. Потребно је са табле удаљити осам кандидата, оставивши само једног – победника на централном пољу. Овај поступак треба обавити у што мањем броју потеза. Потез се састоји или од једног премештања фигуре на суседно поље горе, доле, лево, десно или дијагонално у сва четири правца (као потез краља у шаху – претпостављамо да сви знате бар најосновнија правила у шаху), или у серији скокова једне исте фигуре при чему се у сваком скоку прескаче само једна фигура и то у било којем од праваца: горе, доле, лево, десно или дијагонално. Свака прескочена фигура одмах се скида са табле.
Скоро шездесет година се сматрало да је минималан број потеза за решавање ове загонетке-играчке једнак пет. То решење је дао највећи и најславнији састављач математичких загонетки, логичких задатака, ребуса и шаховских проблема икада, чувени Сем Лојд(1841-1911). Поред Лојдовог решења постоји велики број решења у 5 потеза. У једном од њих, на пример, Тафт у првом потезу може елиминисати чак шест кандидата, Нокса, Џонсона, Лафолета, Кенона, Брајена и Греја (овим редом), међутим, задатак се на овај начин не може решити у мање од 5 потеза.
Шездесетих година двадесетог века установљено је да се задатак о председничким кандидатима може решити у само 4 потеза. Поступак је следећи (али не и једини):
- Тафт прескаче редом Нокса, Џонсона, Лафолета и Кенона;
- Хогс прескаче Брајена;
- Греј прескаче Фербанкса и Хогса;
- Тафт прескаче Греја и стиже у центар табле.
Ово решење навео сам у поменутој рубрици у чланку о загонеткама-премештаљкама у научно-популарном часопису ГАЛАКСИЈА, број 122 (1982). Само месец дана касније у редакцију часописа стигла су четири решења овог проблема – у само три потеза!
Овај догађај био је још један пример дугогодишње оптимизације решења задатог задатка и финале у тражењу минималног решења – светски рекорд је оборен и не може се поправити. То је значило да је Божански број за описану загонетку-премештаљку коначно добијен!
Вредно је поменути имена читалаца који су најзад, после 74 године од поставке проблема, пронашли оптимално решење: Драган Пејчић (Ниш), Симон Чернута (Бовец), Бојан Песек (Марибор) и Милован Ковачевић (Шид). Није никакво чудо што су се међу рекордерима нашла и два Словенца, у то време ГАЛАКСИЈА се читала широм тадашње Југославије и достизала тираж и до 80 000 примерака по броју.
Ево решења (читаоци који желе сами да покушају да пронађу решење у 3 потеза могу да прескоче следеће редове) које се, иначе, битно разликује од ранијих. У прва два потеза ниједан кандидат није елиминисан и они служе за „постављање” кандидата у повољан положај за њихову елиминацију у трећем потезу:
- Греј се помера горе-десно (на поље d5 према шаховској нотацији);
- Брајен се помера доле-лево(на b1);
- Тафт прескаче редом Нокса, Хогса, Брајена, Кенона, Фербанкса, Лафолета, Греја и Џонсона, завршавајући победнички поход у центру табле!
Полазећи од овог основног решења могу се добити и симетрична решења, а и она добијена као лик у огледалу.
Дајемо још неколико Божaнских бројева који се односе на добро познате примере.
Пример 1: Рубикова коцка
Рубикова коцка је 3D комбинаторна загонетка коју је 1974.године креирао мађарски скулптор и професор архитектуре Ерне Рубик. Процењује се да је ова врло популарна играчка која је освојила свет досад продата у 350 милиона примерака. Састоји се од 26 малих коцки обојених у 6 различитих боја и механизма у центру коцке за њихову ротацију. Циљ игре је да се ротацијама малих коцки велика коцка доведе у положај (назван положај истобојних страна) у коме ће свака од 6 страна Рубикове коцке бити исте боје. Поменимо да Рубикова коцка има своје место и у математици, где елементи тзв. групе Рубикове коцке Г(.) представљају потезе мини-коцки.

Математичари су израчунали да је укупан број позиција који може да заузме Рубикова коцка број који се пише са 19 цифара (десет милијарди милијади). Ако се претпостави да се до сваке позиције може доћи за 1 минут, да би се реализовале све позиције било би потребно 82 000 милијарди година! Овако велики бројеви ставили су математичаре и програмере пред велике проблеме у њиховом покушају да нађу минималан број потеза (Божански број) који је довољан да се коцка сложи полазећи од произвољне почетне конфигурације.
Најзад, године 2010, Томас Рокицки и његов тим су дошли до Божанског броја: за слагање Рубике коцке довољноје 20 ротација за било коју почетну позицију. Коришћен је велики број врло моћних Гуглових рачунара који су радили непрестано неколико недеља. Наравно да се у неким врло повољним условима Рубикова коцка може сложити и у мањем броју потеза али, с друге стране, постоје почетне позиције које захтевају не мање од 20 ротација.
Увек када се говори о Рубиковој коцки, неизбежно питање је колики је светски рекорд у брзини у слагању коцке. Тренутно овај рекорд износи невероватних 3,47 секунди а поставио га је Кинез Јушенг Ду 15. новембра 2018. на турниру у кинеском граду Вухуу 2018.
Пример 2: Ханојска кула
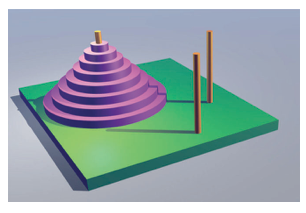
Ханојска кула је веома позната и популарна математичка загонетка-премештаљкакоју је изумео франциски математичар Едуар Лика 1883. године. Састоји се од 3 вертикална клина постављена на плочу и извесног броја дискова раличитих величина. У почетном положају дискови су постављени тако да се мањи диск увек налази изнад већег (као на слици)
Дискови се могу пребацивати (по један у сваком потезу) са једног клина на други на такав начин да је у било ком тренутку на било ком клину мањи диск увек изнад већег. Задатак се састоји у томе да се сви дискови са куле (клин са дисковима у почетном положају) пребаце на неки од друга два клина.
Питање: колики је најмањи број потеза потребан за пребацивање дискова?
Минималан (Божански) број је 2n-1 потеза. Овај број био је познат и пре сто година, али он се односио на тзв. рекурзивни поступак при пребацивању дискова, без доказа да је овај поступак заиста и оптималан. Први коректан математички доказ дао је Д. Вуд у свом раду из 1981, при чему је доказао да је рекурзивни поступак истовремено и оптималан.
Пример 3: Непресецајућа скакачева путања
Скакачева затворена путања или скакачев круг је чувени класичан проблем на шаховској табли 8 x8 (познат још у 9. веку) којим су се бавили и врхунски светски математичари као што су Ојлер, Вандермонд, Лежандр, Де Муавр, Де Монмор и други. То је путања скакача којом он посећује свако поље шаховске табле једном и само једном, а затим се враћа на полазно поље.
Једну варијанту скакачеве путање предложио је Американац Т. Р. Досан 1938. године. Као и код уобичајеног скакачевог круга, скакач не сме посетити ниједно поље више него једном. При овом путу постоје строга ограничења: путања не сме да сече саму себе. Лако се показује да под овим ограничењима скакач не може посетити сва поља шаховске табле. Одавде произилази следећи задатак: Колико највише поља на шаховској табли може да обиђе скакач (рачунајући и полазно поље) а да путања не сме да сече саму себе?
Решење овог проблема у 35 потеза (36 поља) дао је Д. Јардброу у часопису Journal of Recreational Mathematics 1968, али без доказа о оптималности решења. Доналд Кнут, професор Универзитета у Стенфорду и један од највећих светских научника из области компјутерских наука, дао је комплетно решење овог веома тешког проблема осамдесетих година двадесетог века уз помоћ компјутера. Користећи backtrack алгоритам, Кнут је нашао да постоје само 4 основна решења до којих се може доћи испитивањем 3 137 317 289 случајева. Максималан број потеза је 35 (36 поља) и он се не може превазићи. Према томе, у овом примеру Божански број је 36.
Испоставило се да је Јардброуово решење било у потпуности прихватљиво.
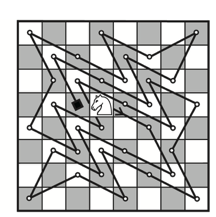
Ово решење је наведено у мојој књизи Mathematics and Chess коју је публиковао познати издавач Dover Publication из Њујорка 1997. године. То је била и прва књига икада написана на енглеском језику која комбиније особине математике и шаха у циљу састављања изазовних проблема и загонетки; и дан-данас сe продаје путем интернета (Amazon, Barnes & Noble).








