Шта се дешава уколико температуру спуштамо ка апсолутној нули? Ваља одмах напоменути да као што сви знамо Трећи закон термодинамике нам каже да се она не може достићи, међутим то нас не спречава да о томе размишљамо.

Данило Николић
У другом делу наше приче дотакли смо се теме статистичког описа природе израженог кроз различите расподеле вероватноће неких догађаја и величина. Напоменули смо да најважнија подела честица јесте на она која се базира на спину, тој загонетној карактеристици материје. Међутим, ако вас неко пита шта је спин, будите слободни да му кажете – својство честице, као и наелектрисање. Занимљиво је да је чак и деци блиско кад им неко каже да честице имају наелектрисање као једну од основних особина, док спин све буни.
Спин је подједнако фундаменталан као и наелектрисање. Просто то је својство честица, повезано са одређеним симетријама које владају у микросвету. Да заобиђемо компликоване формуле и математички опис, оно што је за нас битно јесте да је то чаробно својство изражено Паулијевим принципом, (вероватно) најважнијим принципом природе, израженим кроз такозвану везу спина и статистике. Прошли пут смо напоменули како су дистрибуције вероватноћа окупираности квантног стања (тзв. бројеви попуњености) фундаментално различите за честице полуцелобројног (фермиони) и целобројног спина (бозони).
Међутим, овде се сада поставља питање какве то везе има са суперпроводношћу? И зашто су нам потребне јако ниске температуре да бисмо је постигли? Овде ваља напоменути да многи експерименти показују да суперпроводност постоји и на далеко вишим температурама (у физици ниских температура све преко 10 К (-263°С) је висока температура). И овакав тип материјала неће бити наша тема у овом тренутку. Штавише, испоставља се да не постоји још добра теорија која може да објасни високотемпературску (HTs) суперпроводност.
Бозе – Ајнштајнова представа
Задржимо се на тренутак на квантним статистикама. Као што смо напоменули у претходном тексту једино што разликује колективе слободних фермиона и бозона јесте један минус у функцијама расподеле. И то свега плус или минус 1, међутим последице су драстичне што произилази из самог Паулијевог принципа. Замислимо један број честица на одређеној температури.
Шта је температура? Интуитивно нам је јасно да се температура везује с неком средњом енергијом коју честице система поседују; уколико занемаримо разне нуклеарне и остале унутрашње ефекте доћи ћемо до тога да је температура повезана са тзв. кинетичком енергијом честица, односно енергијом њиховог кретања. У овој поједностављеној слици јасно нам је да виша температура значи и брже кретање наших честица, односно већу енергију. Застанимо за тренутак и замислимо да честице које живе у квантном свету могу бити у такозваним својственим стањима одређених енергија. У овом случају температура је повезана са енергијом стања која насељавају честице.
Дакле, виша температура – виша енергетска стања су попуњена, честице су узбуђеније због те температурске журке. Можда овај опис ради и у друштвима – више температуре више забаве, плажа и журки. Међутим, шта се дешава уколико температуру спуштамо ка апсолутној нули? Ваља одмах напоменути да као што сви знамо Трећи закон термодинамике нам каже да се она не може достићи, међутим то нас не спречава да о томе размишљамо. Такође у пракси температуре се могу спустити до 1 mK па и ниже, што је врло близу нули. Дакле, шта се дешава са честицама у том случају?
Да, погодили сте, оне теже да имају што нижу енергију, односно да окупирају најнижа доступна енергетска стања. И то је кључно место где настаје разлика између бозона и фермиона. То најниже стање је фундаментално различито за ова два типа честица. Као што смо поменули, бозони су дружељубиви и теже да се друже и одлазе у исто стање (тзв. основно енергетско стање, енг. ground state), док су фермиони снобови и морају насељавати различита стања. Дакле, када је основно попуњено, наредни фермион заузима прво наредно и тако даље док се сви не сместе.
Феномен преласка бозона у основно стање на ниским температурама је веома славан у научном свету и познат под именом – Бозе-Ајнштајнова кондензација. Важно је напоменути да овај феномен може постојати у колективима, односно када имамо мноштво честица где њихове колективне особине се разликују од појединачних водећи новим феноменима. Оно што је главна карактеристика оваквог кондензата јесте то што све честице прелазе у једно стање формирајући макроскопску таласну функцију. Такво стање материје „не осећа” отпор кристалне решетке. И убрзо је постало јасно да овакав феномен може стајати у позадини нулте отпорности неких материјала на ниским температурама.
Безобзирни фонони
Нашем читаоцу ће у око упасти једна ствар коју нисам у претходном тексту истакао. Електрони који су носиоци наелектрисања у металима су фермиони. Као што смо видели, њихова снобовска природа им не дозвољава да се кондензују у основно стање као бозони. Шта сада да радимо? Без бриге, овај мали проблем је мучио физичаре безмало пола века. Једноставно било је немогуће електроне уклопити у целу причу. А да бисмо закључили ову нашу причу, неопходно је разумети још један аспект метала, а то је онај део који није електронски.
Као што знамо, атоми се састоје од језгара и електрона. Знамо да неки електрони уз мање или више енергије могу бити отргнути од својих језгара формирајући електрон-јон пар. И то је једна слика којом ми представљамо себи метале. Дакле метал се састоји од кристалне решетке састављене од јона и одређеног броја електрона који мање-више слободно шетају кристалом. У овоме мање-више се крије тајна суперповодности.
Слика 1. Кристална решетка алуминијума (.alamy.com)
Оно што је карактеристично за све решетке јесте то што оне нису статичне. Наиме, јони који леже у чворовима решетке не мирују, већ вибрирају. Оно што је чар квантне механике јесте да и такве вибрације јесу квантоване, тако да вибрације решетке можемо разумети као такође једну скупину честица које су бозонске природе и које се зову – фонони. Будите пажљиви, то није исто што и фотони, који су честице преноснице електромагнетне интеракције, или народним језиком речено – честице светлости. Фононе можемо разумети као честице преноснице звука, односно вибрација кристалне решетке.
У нашем кристалу, дакле, поседујемо електроне који мисле да су слободни и још једну занимљиву врсту честица, поменуте фононе. Зашто је то нама уопште и важно? Одговор је једноставан и интуитиван – оне могу да интерагују. Може доћи по појаве расејања електрона на фононима посредством тзв. електрон-фонон интеракције. И то није тешко замислити – електрон одређеног импулса и енергије слободно шета решетком док се један фонон не испречи и мало га удари. Овај као природно мањи и слабији мора да мења енергију и импулс да бежи не би ли извукао живу главу. Овакав тип бокс меча може се сликовито представити тзв. Фајнмановим дијаграмима расејања.
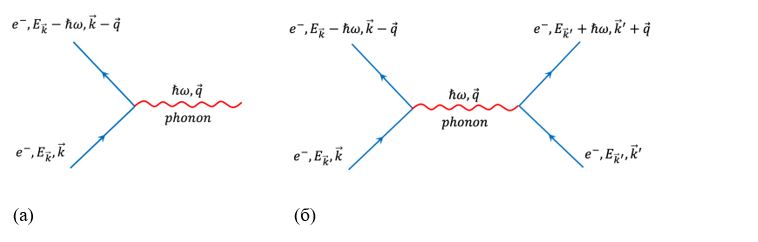
Слика 2. (а) Фајнманови дијаграми електрон-фонон расејања, (б) електрон-електрон интеракција посредована фононом
Једном расејан електрон (пуна плава линија) предаје одређену количину енергије и импулса фонону (црвена таласаста линија) на слици 2а и расејава се. Међутим, како имамо много честица у нашем металу фонон се може сударити са неким другим електроном предавши му тај вишак импулса и енергије (слика 2б). Оно што је занимљиво јесте да оваква интеракција посредована фононима делује ефективно да се електрони привлаче. Одмах ћете ме запитати, а шта је са Кулоновом електростатичком силом која има одбојни карактер у односу на електроне? Да, у праву сте и не само да има, него је поменута интеракција и по интензитету доста јача од ове фононске силе привлачења. Како сликовито ово можемо себи представити?
Електрон пролазећи привлачи многе фононе (који су практично позитивно наелектрисани јони кристалне решетке) себи, што доводи да је густина позитивног наелектрисања око његове путање гушћа. Како електрон иде брзо, иза њега остаје релативно дугачак траг позитивних честица. Ово ефективно позитивно неалектрисање утицаће да неки други електрон буде привучен ту. Погађајте, први је већ одавно отишао. Да, ова интекарција је привлачна, али није занемарива само зато што су електрони већ на великом растојању које више „не осећа” одбојну електростатичку силу. На неки начин можемо закључити да ова електрон-фонон интеракција ефективно утиче на формирање парова електрона, чувених Куперових парова.
Мистерија разбијена – BCS трио
Претходно описани механизам лежи у теоријском објашњењу нискотемпературске суперпроводности познатијем као Бардин-Купер-Шрифер теорија (BCS theory), насталом око пола века после открића суперпроводности. Оно што бисмо се могли запитати јесте – какве везе имају Куперови парови формирани на поменути начин са овим феноменом? Одговор је једноставан: Куперови парови се састоје од парова електрона са спином ½ који заједно дају честицу сада целобројног спина (у овом случају 0, јер се пројекције спинова могу и одузимати, и не бих улазио у ове математичке заврзламе), формирајући такозвано спин-синглетно стање.
Ово стање је сада бозонске природе и омогућено му је да на ниским температурама формира Бозе- Ајнштајнов кондензат који више неће „осећати кристалну решетку” омогућивши ток струје без отпора. Овaj елегантан и изненађујуће добар опис суперпроводности тројици поменутих физичара је донео Нобелову награду за физику 1972. године. Вероватно нисте знали јесте то да је Џон Бардин добио и шест година раније прву Нобелову награду за физику за откриће транзистора, што га смешта међу свега пар двоструких нобеловаца и јединог који је то остварио у физици. Оно што је важно рећи јесте да ови парови никако нису куглице два залепљена електрона. Као што смо рекли, да би ефекат био незанемарив електрони морају бити далеко. Они су парови у тзв. спинском и импулсном простору, не и у координантном.
BCS теорија и дан-данас представља основу у теоријским разматрањима нискотемпературске суперпроводности. За високе температуре она не даје добар опис, али као што сам рекао то питање у физици многочестичних система остаје отворено. А прича о високотемпературској суперпроводности можда неком другом приликом.

Слика 3. Џон Бардин (у средини), Леон Купер (десно) и Џон Шрифер (лево) (researchgate.net)






Jednostavno i lepo napisano, tako da svak, koga interesuje popularizacija nauke može da shvati suštinu fenomena superprovodnosti. Čitalac može jednostavno da poveže u celinu tokove rađanja i funkcionisanja teorije superprovodnosti.
У потпуности сам сагласан; млади физичар изузетно занимљиво и узбудљиво описује веома сложене и запетљане појаве у невидљивој стварности. Сви есеји су му изванредни, надајмосе да че још дуго, дуго писати за Галаксију
Izvrsno! Autor je na veoma, veoma inspirativan i razumljiv način dokučio suštinu problematike superprovodnosti. Kako što sam i očekivao prikazana je značajna uloga Bardina kao jednog od pronalazača tranzistora odakle je munjevitom brzinom krenula tehnološka revolucija kao i doprinos Fajnmanovih dijagrama u ispravnoj formulaciji kvantne elektrodinamike.