Dakle, možemo reći da su fermioni snobovi i da ne vole mnogo da se druže, te stoga neće u isto stanje, dok su bozoni temperamenti mediternaci koji vole druženje i žurke. Nekad se pitam, ko bismo bili mi Srbi u svetu čestica? To vama ostavljam na razmišljanje iako naslućujem odgovor.

Danilo Nikolić
- Mnoštvo je različito – dame i gospodo profesor Gibs
Da bismo nastavili našu priču započetu u prvom nastavku, a u cilju pokušaja da objasnimo lepotu superprovodnosti, reći ćemo par reči o sistemima sastavljenim od mnoštva čestica. Fizičari, kako oni koji se bave njome na istraživačkom nivou, tako i ljudi koji nisu istraživači ali su poklonici prirodnih nauka često su skloni da pod pojmom fundamentalna fizika podrazumevaju teorije elementarnih čestica od kojih je sazdan svet koji nas okružuje.
Jedna od takvih osobina jeste i fenomen
superprovodnosti – kolektiv čestica
koji pokazuje nultu otpornost pri
„prolasku” kroz kristalnu rešetku.
Međutim, nobelovac Filip Anderson u svom znamenitom tekstu More is different (Science, 1972.) ističe – ponašanje velikih i kompleksnih skupina elementarnih čestica, ispostavlja se, ne može biti shvaćeno kao jednostvna ekstrapolacija osobina nekoliko čestica. Ispostavlja se da mnoštvo čestica ispoljava određene osobine umnogome različite od osobina koje poseduju pojedinačno. Jedna od takvih osobina jeste i fenomen superprovodnosti – kolektiv čestica koji pokazuje nultu otpornost pri „prolasku” kroz kristalnu rešetku. Da bismo došli do objašnjenja ovog fenomena krenimo sa istorijom kako to uvek biva.
U prvoj polovini 19. veka pažnju naučnika počinju da privlače toplotne pojave. Razvojem parne mašine i industrijske revolucije postalo je jasno da je značaj toplotnih mašina veoma veliki, čime se na noge postavlja nauka o prenosu toplote – termodinamika. Pionirom termodinamike smatra se Nikola Karno čiji rad je direktno bio motivisan povećanjem efikasnosti toplotnih mašina što je smatrao osnovnim uslovom koji može obezbediti pobedu Francuske u Napoleonovim ratovima. Kako bilo, Napoleon je poražen na kraju.
Vremenom se shvatilo da nauka o toploti ima određene univerzalne principe koji se ne tiču samo rada toplotnih mašina (tzv. toplotni ciklusi), tako da termodinamika svoje prve definicije dobija sredinom 19. veka kroz radove lorda Kelvina i Rudolfa Klauzijusa, da bi svoj vrhunac doživela kroz statističku definiciju Maksvela i Bolcmana. Sva ova imena su vrlo dobro poznata poštovaocima prirodnih nauka.
Međutim, jedan od glavnih heroja u našoj današnjoj priči jeste jedan drugi fizičar – Džosaja Vilard Gibs (Josiah Willard Gibbs, 1839-1903.), ime možda manje poznato od prethodno pomenutih, a koje je zaokružilo priču započetu radovima Maksvela i Bolcmana. Iako njegovo ime ne zvuči poznato svima, ja ću vam reći da je to jedan od najvećih fizičara ikada. Teorijski koncept koji je on razvio pretrpeo je sve revolucije u nauci do danas u manje-više neizmenjenoj formi – koncept usrednjavanja što predstavlja centralno mesto statističkog opisa prirode. Motivisan radovima pomenute gospode Maksvela i Bolcmana koji zasnivaju statistički opis (klasična Maksvel-Bolcmanova statistika), Gibs ga matematički zaokružuje 1902. uvodeći pojam statističkog ansambla.
Pošto nam namera nije da uranjamo u komplikovane matematičke račune, pokušaću u par rečenica da objasnim pojam ansambla na način nadam se razumljiv našim čitaocima. Razmotrimo vazdušni pritisak. Intuitivno je jasno da je on povezan za broj sudara čestica vazduha (recimo da su to sve identični atomi) sa zidovima suda. Postavlja se pitanje kada merimo pritisak nekim barometrom, šta mi tačno merimo? Da, upravu ste, merimo sudare čestica i površine sonde našeg instrumenta. Pitanje je koji broj sudara merimo? Da li detektujemo svaki pojedinačni sudar sa sondom?
Ne, naš instrument ne može imati tu rezoluciju, naš instrument meri neki srednji broj sudara u nekom vremenskom intervalu. Zato i ima potrebe i jedinog značaja u termodinamici konstantno govoriti o nekim srednjim vrednostima. Međutim, pitanje je šta će nam neki ansambli tu? Jednostavno, naše teorije ne mogu da usrednjavaju po vremenu. Sistemi su i suviše kompleksni da bismo mogli sve jednačine kretanja pojedinačnih čestica da rešimo i da dobijemo vremensku evoluciju sistema.
Zato veliki Gibs nudi alternativu. Zamislimo da imamo sistem čestica gasa (recimo vazduha) određene zapremine i temperature. Pretpostavimo da je i energija gasa fiksirana i neka nas interesuje recimo pritisak, odnosno srednji broj sudara sa granicama naše zapremine. Šta da radimo kad ne znamo vremensku evoluciju sistema? Pa Gibs nam daje recept – usrednji po svim mogućim mikroskopskim realizacijama. Kako to mislite, profesore? Pa, lepo ispitaj koje sve konfiguracije čestica u tvom sudu će zadovoljiti uslove zadate temperature i energije u našem sudu. Ujedno, ovo je i definicija statističkog ansambla.
Malo ću ovde zaroniti u matematiku
pa ću vam reći da jednoj konfiguraciji
odgovara jedna tačka u faznom prostoru,
koji ima 6N dimenzija, gde je N broj
čestica! Uvrnuto, reći ćete. A ja kažem
– da, uvrnuto, ali mene više leđa ne bole,
što bi rekla baka na reklami.
Dakle, statistički ansambl predstavlja skup svih kopija, svih mikroskopskih scenarija koji će zadovoljiti makroskopski zadate parametre. Dakle, kao da zaledimo 50 konfiguracija čestica koje će nam dati tu i tu energiju i temperaturu. Naravno podrazumevamo i da je broj čestica zadat. Malo ću ovde zaroniti u matematiku pa ću vam reći da jednoj konfiguraciji odgovara jedna tačka u faznom prostoru, koji ima 6N dimenzija, gde je N broj čestica! Uvrnuto, reći ćete. A ja kažem – da, uvrnuto, ali mene više leđa ne bole, što bi rekla baka na reklami. Napomenuo bih samo da energija ne mora biti fiksirana, kao ni broj čestica. Ali ne bih više o ovome debatovao, jer sve dalje bi nas bacalo u matematički opis, što nije cilj na ovom mestu.

Slika 1. Maksvel-Bolcmanova raspodela čestica po brzinama za različite gasove (levo) i Džozaja Vilard Gibs (desno) (preuzeto sa Vikipedije)
- Kvantne komplikacije – nastupa Pauli
Kao što smo videli u prvom delu smo se bavili klasičnim gasom. I stvari su već počele da deluju komplikovano (moramo da mislimo u 6N dimenzija). Međutim, mi smo avanturisti i ne volimo jednostavne stvari, tako da život može biti još komplikovaniji. Da, kvantne komplikacije su ono što želimo.
Podsetimo se na trenutak da u kvantnoj mehanici centralno mesto zauzima talasno-čestični dualizam. Dakle, čestice se na neki magični način nekada ponašaju kao talasi određenih talasnih dužina. Kada su visoke temperature čestice su srećne i vrlo razdragane, tako da možemo reći da su dobro lokalizovane i na plesnom podijumu rastojanja su velika, odnosno da ih možemo smatrati kuglicama. Međutim, snižavanjem temperature njima se spava, tako da se polako „guraju” jedna do druge do trenutka kada su rastojanja među njima u proseku uporediva s talasnim dužinama dodeljenih talasa i tada dolazi do omiljene pojave mnogih fizičara s magičnim imenom – interferencija.
Centralno mesto naše priče u ovom
odeljku zauzima možda i najvažniji
princip prirode, za koji nemamo
objašnjenje pored toga da ima univerzalnu
važnost – Paulijev princip isključenja.
Uslovno rečeno, talasne funkcije se preklapaju ispoljavajući nove – kvantne osobine. Dakle, možemo očekivati na niskim temperaturama ispoljavanje drastično dručačijih osobina gasova nego na sobnoj temperaturi, a to sa sobom vuče i novu fiziku, fiziku kvantnih statistika.
Centralno mesto naše priče u ovom odeljku zauzima možda i najvažniji princip prirode, za koji nemamo objašnjenje pored toga da ima univerzalnu važnost – Paulijev princip isključenja. Kao što znamo svaki elektron ima svoju masu, naelektrisanje, ali i nešto što se zove spin. Ako bih na bilo koji način pokušao da ga oslikam pogrešio bih. Uobičajeno je da se on zamišlja kao rotacija elektrona oko svoje ose, što je malo besmisleno ukoliko razumemo da elektron nije kuglica.
Zato ću ja reći da je spin fundamentalna karakteristika čestica kao što je recimo naelektrisanje. Spin elektrona može imati dve vrednosti (tzv. projekcije spina) , gde je potonji znak tzv. Plaknova konstanta (ili preciznije redukovana Plankova konstanta). I to važi za sve elektrone u univerzumu. Međutim, elektroni nisu jedine čestice u prirodi. Postoje čestice i sa drugim izborom ovih projekcija i to nas vodi jednoj univerzalnoj podeli – čestice sa polucelobrojnom projekcijom spina zvane fermioni, dok su njihovi drugari sa celobrojnim spinom ( ) poznati u društvu čestica kao bozoni. Ali kakve to veze ima sa Paulijem, tim simpatičnim bucom iz Austrije?
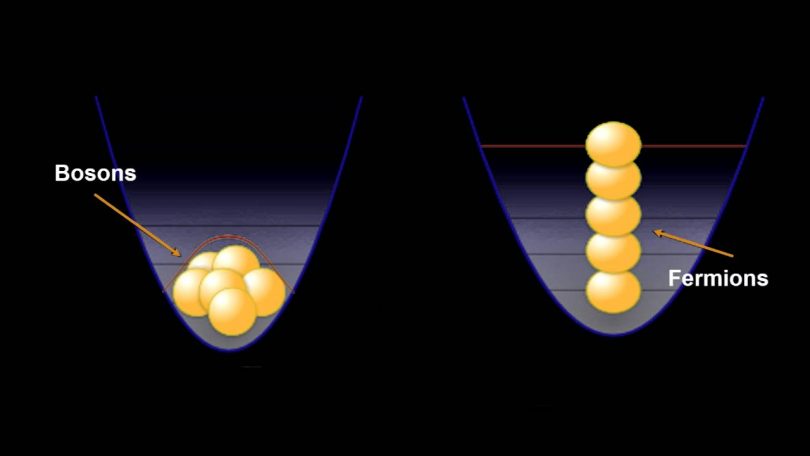
Kao što znamo čestice mogu imati različite energije. Svakoj od tih energija u kvantnoj mehanici odgovara jedno stanje (nekada i više, ali radi jednostavnosti pretpostavimo da je samo jedno). Dakle, talas može imati različite forme, sa različitom energijom. Pauli kaže sledeće – samo dve (ili više) čestice sa celobrojnim spinom se mogu nalaziti u istom kvantnom stanju, dok je za one druge to strogo zabranjeno. Dakle, možemo to reći u maniru da su fermioni snobovi i da ne vole mnogo da se druže, te stoga neće u isto stanje, dok su bozoni temperamenti mediternaci koji vole druženje i žurke. Nekad se pitam, ko bismo bili mi Srbi u svetu čestica? To vama ostavljam na razmišljanje iako naslućujem odgovor.
Verovali ili ne, kao što rekoh ovaj jednostavan princip je možda najvažniji i najuniverzalniji princip prirode! Ali kakve to veze ima s našom početnom pričom? I te kako ima. Iz gornjeg iskaza vidimo da kvantna stanja se ne popunjavaju uvek na istovetan način, odnosno gorepomenuta interferencija nije identična za fermione i bozone, što se fundamentalno odražava u činjenici da Maksvel-Bolcmanova statistika koja važi za klasične gasove, nije više na snazi i biva zamnjena dvema novim tzv. kvantnim statistikama – Fermi-Dirakovom (pa otuda fermioni) i Boze-Ajnštajnovom (bozoni). Ove statistike se razlikuju samo za jedan minus, ali posledice su fantastične! A kakve to veze ima sa našom pričom o superpovodnosti videćemo u sledećem i poslednjem delu naše priče.

Slika 2 Volfgang Pauli (levo) i Nils Bor (desno) se igraju kineskom čigrom (tippe top). Stiče se utisak da veliki umovi ostaju deca tokom celog svog života (preuzeto sa Cosmolearning.org)





Bajkovito, maštovito i meni slikovito,
Citat:
„Teoretičari postižu svoje vrhunske životne domete najčešće u mladosti; kod njih kreativni sokovi krenu rano, a počnu da presušuju već sa petnaest godina – tako se, barem, čini. Potrebno je da teoretičar ima samo onoliko znanja koliko mu je potrebno, i ne više od toga; dok je mlad, još nije poguren pod teretom suvišnog intelektualnog prtljaga koji se vremenom nagomilava“.
Svedoči – LION LEDERMEN
Veoma inspirativan i intrigantan tekst. Veoma se retko u naučnim raspravama sa ozbiljnom tematikom može videti ovako duhovit i koncizan pristup. želeo bih da se u sledećem nastavku baci akcenat na postizanje superprovodnosti na višim temperaturama što bi imalo dalekosežne benefite na zemlji kao i moguće futurističke projekte u kosmosu s obzirom na temperature koje tamo vladaju.