Петербуршки парадокс први је разматрао Николаус Бернули 1713. и актуелан је и у данашње доба, специјално за математичаре и економисте који се баве теоријом одлучивања. Стандардна верзија изведена је из игре из Санкт Петербурга у којој играч А (казино у модерном добу) и играч B бацају исправан новћић („глава”/„писмо”) све док се не појави писмо. Ако је n број узастопног појављивања главе, играч А исплаћује играчу B 2n-1 круна.

Проф. др Миодраг Петковић
Kористећи основне елементе теорије вероватноће произилази да је износ у крунама који би играч B реално могао да очекује (једнак математичком очекивању) бесконачно велики! Kолико новца играч B би требало да уложи да би играо ову игру? Парадокс произилази из противречност између оног износа који је играч B спреман да плати да би играо ову лутријску игру и (теоријски) бесконачног износа који очекује.
Многи математичари из 18. и 19. века бавили су се проблемом познатим као Петербуршки парадокс. Проблем је формулисао швајцарски математичар Николас Бернули (1687-1759) у писму Пјеру Рејмону де Монмору 9. септембра 1713. године. Међутим, парадокс је добио име по анализи коју је разрадио Николасов рођак Данијел Бернули (1743-1794) који је један део живота провео у руском граду Санкт Петербургу. Он је своју анализу објавио 1738. године у часопису Commentarii Петербуршке академије. Парадокс се односи на математичко очекивања при лутријској игри бацања новчића.
Двојица играча А (рецимо казино) и B играју игру под следећим условима: При бацању исправног новчића (глава/писмо) играч А врши исплату играчу B при сваком бацању када падне „глава”. Игра се завршава када се први пут појави „писмо”. Ако се глава појави у првом бацању, А плаћа играчу B једну круну; ако се појави у другом бацању, А исплаћује две круне; ако се појави у трећем, четири круне и тако даље, удвостручавајући суму сваки пут. Kоначно, ако се глава појави у n-том бацању, играч B добија 2n-1 круна од играча А. Претпоставка је да се игра може наставити бесконачно. Kолики износ може да очекује играч B?
Питање се може формулисати и овако: „Kолико новца би играч B требало да уложи да би играо ову игру”?
Вероватноћа да играч B добије једну круну износи 1/2, да добије две круне 1/4 и тако даље. Дакле, укупан број круна који би играч B реално могао да очекује (једнако математичком очекивању) износи
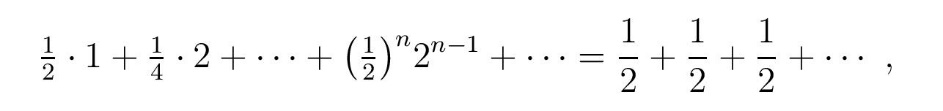
што даје бесконачан збир! Неки аутори описују да се у овој игри на срећу збир приближава бесконачности, а не да је бесконачан узимајући у обзир реалну ситуацију да није могуће физички обавити бесконачан број бацања новчића.
Парадокс произилази из противречности између оног износа који је играч B спреман да плати да би играо ову лутријску игру и (теоријски) бесконачног износа који очекује. Р. Мартин у књизи The St. Petersburg Paradox” (The Stanford Encyclopedia of Philosophy, Stanford University, 2004) пише: „У строго логичком смислу, Петербуршки парадокс није парадокс јер се не изводи никаква формална контрадикција. Међутим, тврдња да рационални власник казина ризикује (истина с врло малом вероватноћом) да плати милионе, чак милијарде, изгледа апсурдно”. Мартин, такође, наводи да би само мали број играча B платило 25 долара да уђе у ову игру.
Још је Данијел Бернули изјавио да, иако математичко очекивање заиста даје бесконачан износ, играч А (у модерном добу казино) би радо стартовао са 20 дуката. Извесно је да ће играч B освојити веома скроман износ. Објашњење је једноставно: вероватноц́а да играч B не освоји више од 2 долара је 1/2, а да не освоји више од 4 долара је 3/4. Вероватноћа да при бацању новчића глава узастопце падне (рецимо) 10 пута износи 1/(210 )= 1/1024 или око 0,1%.
Овај неочекиван резултат привукао је пажњу многих математичара, укључујући браћу Данијела и Николаса III Бернулија и велику групу француских математичара. Жан ле Рон Даламбер (Jean le Rond D’Alambert, 1717-1783), један од највећих математичара тог доба, писао је Жозефу Лују Лагранжу, другом славном француском математичару: „Ваша књига о играма чини ме веома нестрпљивим да нам дате решење Петербуршког проблема, који ми се чини нерешивим на основу познатих принципа”. Француски математичари Kондорсе (Nicolaus Condorcet, 1743-1794) и Поасон (Simèon Poisson, 1781-1840) сматрали су да играч А улази у аранжман који је за њега неповољан и да игра садржи неке контрадикције.
С друге стране, Жозеф Бертран (Joseph Bertand, 1822-1900) je тврдио да је ова теорија (и резултат који је горе дат) сасвим коректна и једино услови игре дају предност играчу B, што доводи до неочекиваног резултата. Он је сматрао да, ако би се број бацања ограничио, тада би шансе двојице играча биле другачије. На пример, за сто бацања играч B би морао да уложи 15 круна да би играо (сума једнака математичком очекивању његовог добитка) и тада би његов ризик да изгуби био већи. Услови игре би и даље фаворизовали играча B, што проистиче из могућности великог добитка, мада је вероватноћа за то мала. Улог играча B зависи од броја бацања које мора А да изведе. Ако је тај број n, Бертран је израчунао да улог играча B треба да буде
![]()


Епитаф Николасу Бернулију (1759), Портрет Данијела Бернулија
(1725) (CC-BY-SA-4.0)
Неки математичари понудили су решење које се заснива на чињеници да је срећа играча у пракси коначна па, према томе, његов добитак не може бити неограничен. Гроф Де Бифон (De Buffon, 1707-1788) је, чак, извео емпиријски тест како би пронашао просечну суму. Данијел Бернули је трагао за решењем преко свог принципа моралног очекивања, у складу с којим је заменио износе
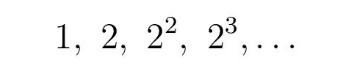
са
![]()
Заправо, он је сматрао да вредност добитка није само у броју освојених круна, већ се састоји и од задовољства услед добитка. Према његовом резоновању, настала срећа због добитка од 100 милиона круна неће се удвостручити ако се добије још 100 милиона. Уопште, ако је а почетни износ а додатни износ b, користећи свој принцип моралног очекивања Данијел Бернули је пораст среће настале услед добитка додатног износа б изразио интегралом
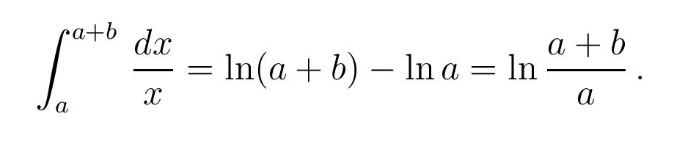
На пример, у случају удвостручавања неког добитка (суме новца или броја неких предмета), увећање среће по D. Бернулију биће око 70% а не 100% јер је
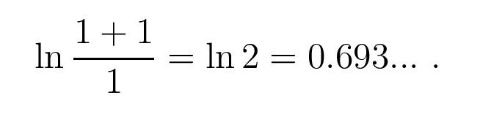
Покушајте себе да тестирате: ако сте добили нови аутомобил, а потом још један истих карактеристика, да ли ћете бити двоструко срећнији?


Санкт Петербург (Pixabay)
Данијел Бернули је Петербуршки парадокс прокоментарисао следећим речима; „Одређивање вредности неке ствари не сме бити засновано на цени, већ на корисности коју она доноси… Нема сумње да је добитак од хиљаду дуката значајнији за сиромаха него за богаташа, иако и један и други добијају исти износ”.
Међу различитим приступима да се проблем модификује да би се добио коначан одговор, један од најприхватљивијих је предложио Габријел Kрамер (око 1730). Kрамер је пошао од претпоставке да играч А поседује ограничену суму новца, рецимо 224=16.777.216 круна. Тада постоји вероватноћа 1/(2n ) да ће играч B добити 2n-1 круна у n-том бацању само док је n < 25; након тога он може добити само 224 круна. Kако је
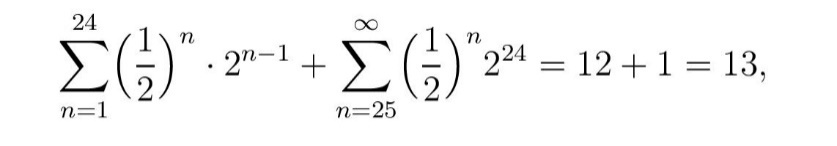
очекивање играча B је 13 круна, што је разумна сума. Интересантно је поменути да би у случају данас најбогатије особе на свету Илона Маска (чије је богатство у априлу 2022. процењено на 265 милијарди долара) улог у игри Kрамеровог типа био само 20 (= 19 + 1) долара јер је после 38-ог бацања добитак константан и износи „само” 238 долара (једнако Масковом богатству, 265 милијарди ≈ 238 ), али је број бацања новчића теоријски бесконачан. У то се можемо лако уверити ако број 24 у претходној формули заменимо бројем 38.
Постоје више варијанти Петербуршког парадокса конструисане увођењем разних услова у игри који доводе до различитих исхода, при чему се користе разноврсни алати и анализе из различитих дисциплина, почев од економије, филозофије, социологије, вероватноће, па све до Ремзијеве теорије и психологије (прецизније, људског понашања у рискантним ситуацијама која донекле имају везе са популарним квизовима типа „Kако постати милионер” или понашањем брокера на берзи када је у питању избор између понуђених алтернатива). Детаље у вези Петербуршког парадокса дискутовали су History of the Mathematical Theory of Probability, London, 1865), E. Kamke, Einführung in die Wahrscheinlichkeitstheorie, Leipzig, 1932), M. Kretik (Mathematical Recreation, New York, 1953), Rauz Bol и Kokseter (Mathematical Recreations and Essays, New York, 1987) и други.








