Логично је претпоставити да се као прва цифра у довољно дугим листама нумеричких података подједнако појављују цифре од 1 до 9. Међутим, још 1881. Симон Њукомб је приметио парадоксалну појаву да се број 1 јавља као прва цифра у скоро 30% разматраних листа нумеричких података, док се проценат јављања осталих цифара смањује са растом цифара од 1 до 9! Овај неочекиван феномен прве цифре, који је касније темељно изучавао физичар Френк Бенфорд, тема је овог прилога.
Проф. др Миодраг Петковић
Kолико се често као прва цифра у довољно дугим листама нумеричких података појављују цифре од 1 до 9? Логично је очекивати да је фреквенција појављивања ових цифара приближно иста. Међутим, најпре је математичар и астроном Симон Њукомб приметио 1881, а затим је физичар Френк Бенфорд (General Electric Co.) у свом раду The Law of Anomalous Numbers из 1938. објавио да се јавља необична фреквенција цифара од 1 до 9 у листама нумеричких података, не само при извођењу експеримената у физици и инжењерским дисциплинама, већ и у географским подацима (нпр. површине острва и држава, дужине река, број становника), берзанским подацима, бројевима кућа у дужим улицама итд. Број 1 се јавља као прва цифра у скоро 30% разматраних случајева (у Бенфордовом истраживању било их је 20.229), док се проценат јављања осталих цифара смањује са растом цифара од 1 до 9! Најбоља провера се може запазити прелиставајући логаритамске таблице. Због тога се описано понашање често назива закон прве цифре или феномен водеће цифре.
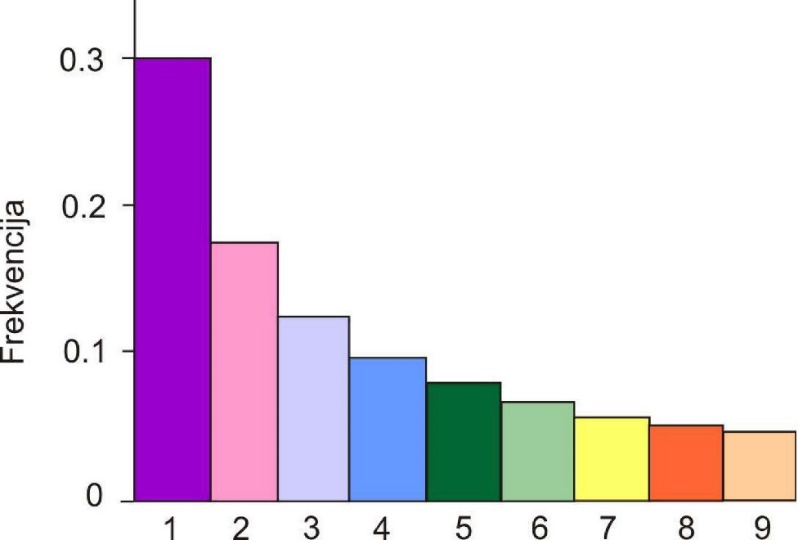
Сл. 1 Фреквенција појављивања цифара као водеће цифре
Бенфорд се посветио овом проблему и после испитивања великог броја нумеричких података различитог типа дошао је до емприријске формуле за вероватноћу појављивања P(n) цифре n као прве цифре, која гласи
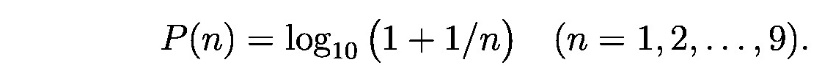
Овај закон назван је Њукомб-Бенфордов закон, мада се у литератури чешће среће назив Бенфордов закон. Теоријске фреквенције (према последњој формули) приказане су графички на слици 1, а нумеричке вредности су дате у табели 1 (видети, такође, последњу колону табеле 2).
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
P(n) |
30.1% |
17.6% |
12.5% |
9.7% |
7.9% |
6.7% |
5.8% |
5.1% |
4.6% |
Табела 1 Теоријске фреквенцијције бројева од 1 до 9 (у %)
Бенфордов закон се још назива и „законом моћи” или „законом величине”. На пример, велика језера су ретка а мала знатно чешћа. Слично, у првом интервалу 1-100 има 11 Фибоначијевих бројева, а у следећим интервалима [101-200, [201-300] и [301-400] само по један. Подсећамо да су први бројеви Фибоначијевог низа
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377…
Kод овог низа сваки члан, изузев прва два, једнак је збиру два претходна члана. Ево још пар сличних примера: добро познати бесконачни низови, као што су факторијели n! и степени броја 2 (али и других бројева) задовољавају Бенфордов закон тачно или асимптотски.
Kао добра илустрација може послужити и улагање у акције неке компаније. Једноставности ради, нека је почетна вредност акција 100 долара и годишња камата 10%. Прва цифра је 1. Следеће године стање на рачуну је 110 долара, дакле 1 је поново водећа цифра. Да би се дошло до вредности акција од 199 долара потребно је да прође 88 месеци. После тога вредност акција се изражава бројевима који почињу цифром 2, од 200 до 299, и за то су потребна 52 месеца. Цифра 9 јављаће се само 12 месеци (вредност акција од 900 до 999).
Од интереса је следећа примена Бенфордовог закона. Засновано на прихватљивој претпоставци да су људи који измишљају бројеве склони да своје цифре расподељују прилично равномерно, особе које желе да кривотворе податке при пријављивању пореза или сличним преварама, настоје да у својим пријавама упишу бројеве тако да се све цифре јављају приближно подједнак број пута. Ова превара се детектује применом Бенфордовог закона према коме се фреквенције појављивања цифара разликују. Према истраживањима Хала Варијана са Универзитета Kалифорнија у Берклију, Бенфордов закон могао би се користити за откривање могућих превара у социо-економским подацима који се подносе у прилог одлукама у области јавног планирања.
Интересантан је пример у коме се посматрају водеће цифре висина 58 највиших зграда на свету, видети табелу 2. Водеће цифре висина зграда понашају се приближно по Бенфордовом закону, и то независно да ли су висине изражене у метрима (m) или стопама (ft).
5858
|
Vodeća cifra n |
m |
ft |
Po Benfordovom zakonu |
||
|
Broj zgrada sa vodećom cifrom visine n |
% |
Broj zgrada sa vodećom cifrom visine n |
% |
||
| 1 | 24 | 41.4 % | 16 | 27.6 % | 30.1 % |
| 2 | 9 | 15.5 % | 8 | 13.8 % | 17.6 % |
| 3 | 7 | 12.1 % | 5 | 8.6 % | 12.5 % |
| 4 | 6 | 10.3 % | 7 | 12.1 % | 9.7 % |
| 5 | 1 | 1.7 % | 10 | 17.2 % | 7.9 % |
| 6 | 5 | 8.6 % | 4 | 6.9 % | 6.7 % |
| 7 | 1 | 1.7 % | 2 | 3.4 % | 5.8 % |
| 8 | 4 | 6.9 % | 5 | 8.6 % | 5.1 % |
| 9 | 1 | 1.7 % | 1 | 1.7 % | 4.6 % |
| 58 | 58 | ||||
Табела 2 Водеће цифре висина највиших зграда на свету (Wikipedia)
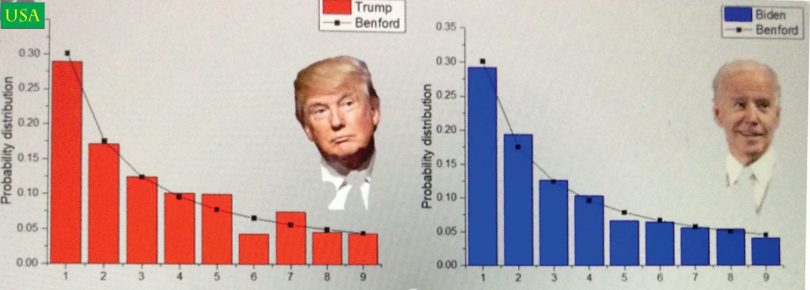
Француз Будевин Рукема је само неколико дана после оспораваних парламентарних избора јуна 2009. године у Ирану обавио истраживање на основу фреквенције водећих цифара у бројевима који представљају резултате избора по разним регионима и закључио да је број гласова у изборима за председника коригован навише. С друге стране, одступања података са председничких избора у САД 2020. од оних добијених помоћу Бенфордовог закона била су минимална, што се може видети из насловне илустрације овог прилога. Ипак, истраживања на Kолумбија универзитету последњих година показала су да примена Бедфордовог закона за откривање превара на изборима није довољно веродостојна уколико постоји велики број изборних јединица које имају мали број гласача.
Наведимо једну интересантну и корисну примену Бенфордовог закона: однедавно овај закон се примењује као један од метода при утврђивању плагијата у „научним радовима” у којима се, на пример, резултати експеримента фалсификују. Плагијатори, пре него што одлучите да се бавите овим неакадемским криминалом, најпре добро проучите Бенфордов закон!
(Насловна илустрација Дијаграмска анализа (S. Kuestenmacher/twitter.com)