Manje je poznato da se naš slavni matematičar Mihajlo Petrović bavio i popularizacijom nauke, pre svega matematike, što je uostalom bio manir svih velikih naučnika – traganje za lepotom u nauci. U ovom prilogu biće izložena dva izazovna matematička problema koja su privukla pažnju velikog Mike Alasa.

Prof. dr Miodrag Petković
Ove godine navršilo se 150 godina od rođenja akademika Mihaila Petrovića-Alasa (1868-1943), jednog od najvećih srpskih naučnika i osnivača srpske matematičke škole. Osim matematike, bavio se i drugim naučnim disciplinama, pre svih fizikom, hemijom i biologijom, nastojeći da ih poveže univerzalnim metodama. Mihailo Petrović je bio jedna od najpopularnijih ličnosti starog Beograda, poznat kao Mika Alas, nadimak koji je dobio kao izvrsni poznavalac ribolova, ali i putopisac, filozof i muzičar: svirao je violinu, a krajem 19. veka osnovao je sviračko društvo pod nazivom „Suz”. Kao pasionirani putnik, proputovao je kroz sve evropske zemlje, a obišao je i severni i južni pol.
Izneti podaci su uglavnom dobro poznati širokom krugu poštovalaca lika i dela Mihaila Petrovića. Manje je poznato da se on bavio i popularizacijom nauke, pre svega matematike, što je uostalom bio manir svih velikih naučnika – traganje za lepotom u nauci. U ovom prilogu biće izložena dva izazovna matematička problema koja su privukla pažnju velikog Mike Alasa. Po mišljenju autora ovih redova, oba problema su dovoljno interesanta za širok krug ljubitelja elementarnih ali lepih i ne tako lakih matematičkih zadataka.
Trećina zapremine
Pitanje je jednostavno: Kako izmeriti trećinu zapremine posude oblika kocke bez ikakvih oruđa za merenje?
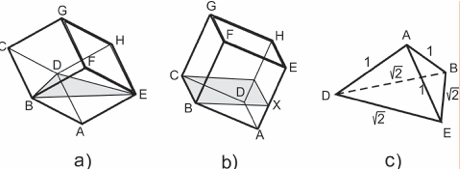
Pretpostavimo da je zapremina suda oblika kocke jedan litar, što očigledno ne utiče na rešenje. Pred nama je zadatak kako da odmerimo 1/3 litra vode. Postavimo sud na teme A (sl. a) i nalivajmo u njega vodu sve dok se površina vode ne izjednači sa ravni trougla EBD. U tom momentu voda zauzima 1/6 zapremine suda, što se može lako dokazati koristeći sliku c. Ne prolivajući vodu, postavimo posudu na ivicu AD (sl. b). Nagnimo sud (oslonjen na ivicu AD) tako da površina vode „ prolazi” kroz ivicu BC. Označimo na ivici AE tačku X koja predstavlja „presek” ove ivice i površine vode. Očigledno je |AX|=|AE|/3, pri čemu |FG| označava dužinu duži FG. Postavimo sada sud na osnovu ABCD i dolijmo vodu do tačke X; na taj način izmerena je 1/3 litra vode.
Šahovski paradoksi
Sledećim interesantnim geometrijskim paradoksom bavili su se razni matematičari, uključujući i Mihaila Petrovića-Alasa. Posmatraćemo dva slučaja, u zavisnosti od parnosti broja n, koji označava dimenziju šahovske table n x n.
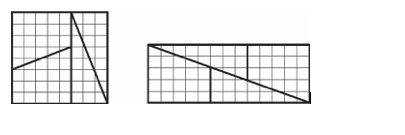
n je parno: Šahovska tabla dimenzija 8 x 8 isečena je na četiri dela (dva trougla i dva trapeza), kao što je pokazano na slici levo. Od ovih delova sastavljen je pravougaonik dimenzije 13 x 5 (slika desno). Dakle, od kvadrata površine 8 x 8=64 dobijen je pravougaonik površine 13 x 5 = 65, što dovodi do paradoksa
64 =65!?
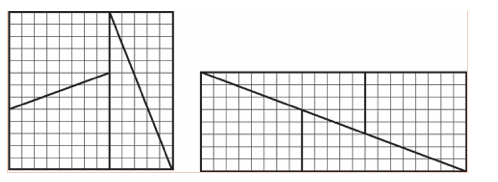
n je neparno:Na sličan način kao u gornjem primeru, od „šahovske table” dimenzije 13 x 13 i površine 169 (slika levo), isecanjem na četiri dela (dva trougla i dva trapeza) i ponovnim sastavljanjem dobijen je pravougaonik dimenzije 21 x 8 površine 168 (slika desno). U ovom slučaju dobijamo geometrijski paradoks
169=168 !?
Primetimo da se u ovim primerima javljaju brojevi 5, 8,13, 21. Ako se još malo potrudimo nalazimo da je 5+8=13, 8+13=21. Čitaocima koji su proučavali (ili proučavaju) nizove odmah će prepoznati (ili bar posumnjati) da je u pitanju niz kod koga se svaki član (osim prva dva) dobija kao zbir prethodna dva, dakle
Fn+1 = Fn + Fn-1, F1 = 1, F2 = 1, n≥2.
Ova relacija definiše poznati Fibonačijev niz {Fn} čiji su prvi članovi
1, 1, 2, 3, 5, 8, 13, 21, 34…
Primećujemo da je u prvom primeru 13 x 5 – 82=1, a u drugom 21 x 8-132 = -1. Nije teško dokazati da u opštem slučaju važi identitet
Fn+1Fn-1 – Fn2 = (-1) n (n > 0) (*)
koji je još pre trista godina izveo Đovani Kasini (1625-1712) , poznati italijanski matematičar, astronom i inženjer.
U prvom primeru dobijen je kvadrat više, a u drugom kvadrat manje. U opštem slučaju, uzimajući Fibonačijeve brojeve Fn-1, FniFn+1, konstruiše se kvadrat dimenzije Fn x Fn, deli se na 4 dela (dva trougla i dva trapeza) od kojih se sastavlja pravougaonik dimenzije Fn-1xFn+1.Prema Kasinijevom identitetu (*) jedan kvadrat će biti dobijen ili izgubljen, zavisno od toga da li je n paran ili neparan broj. Pokušajte sa kvadratom 21 x 21 i pravougaonikom 13 x 34.
Kasinijev identitet objašnjava konstrukciju kvadrata i pravougaonika, ali ne objašnjava dobitak ili gubitak jednog malog kvadrata, dakle ostaje pitanje kako objasniti navedene paradokse.
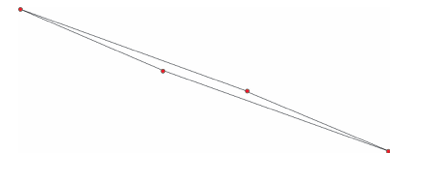
Posmatrajmo prvi primer u kome je podeljena standardna šahovska tabla. Kako je dobijen kvadrat više? Paradoks nastaje usled činjenice da se ivice četiri dela, koje leže duž dijagonale formiranog pravougaonika, ne poklapaju sasvim. Ova dijagonala nije duž već uski romboid (slika gore) čiji je oštar ugao približno jednak 1 stepen i 15 minuta.
Samo pri vrlo tačnom crtanju moguće je zapaziti ovaj ugao. Koristeći trigonometriju ili analitičku geometriju lako se pokazuje da je površina „skrivenog” romboida upravo 1. „ Prisustvo” ovog romboida u pravougaoniku objašnjava višak od jednog polja. Na gornjoj slici nacrtan je pomenuti romboid, ali samo približno, sa nešto uvećanim oštrim uglom da bi se izbeglo poklapanje ivica.
Ime Kasini koje smo pomenuli u vezi identiteta (*) nije poznato ni većini matematičara, ali ipak zvuči tako poznato, naročito onima koji prate kosmička istraživanja. Zajedničkim snagama NASA, Evropske svemirske agencije i Italijanske svemirske agencije krenulo se jula 2004.sa projektom Cassini (kompletan naziv je Cassini-Huygens projekat) s ciljem da satelit lansiran u pravcu Saturna uđe u orbitu ove planete i prouči ovu najneobičniju planetu Sunčevog sistema. Satelit je neprekidno slao izvanredne slike 13 godina, da bi se konačno u septembu 2017. završila njegova uspešna misija padom na tle Saturna. Na slici je prikazana jedna od najatraktivnijih slika poslata sa „Kasinija”.

Slika Saturna poslata sa satelita „Kasini” (Vikipedija)









Nisam nimalo upućen u matematiku, ali sa uživanjem čitam kratke eseje prof. Petkovića. Sve dok ne naiđu jednačine i formule, Ovo štivo je – ako sam dobro razumeo – namenjeno srednjoškolcima i visokoškolcima. U krajnjemm, na dobitku su svi čitaoci Galaksije zato što svoje umove podvrgavaju najstrožem logičkom propitivanju – matematici. Mihailo