Проблем се односи на број једнаких сфера које додирују дату сферу исте величине. Настао је након дискусије чувених математичара Исака Њутна и Дејвида Грегорија 1694. године. Чувен је из више разлога: 1) формулација је не само елегантна, геометријски атрактивна, већ и врло једноставна; 2) упркос једноставне поставке, било је потребно 250 година да се дође до решења.

Проф. др Миодраг Петковић
Паковање сфера, познато као Грегори-Њутнов проблем или проблем додирујућих сфера, односи се на број једнаких сфера које додирују дату сферу исте величине. О овоме су доста су дискутовали Дејвид Грегори (David Gregory, 1659-1708) и Исак Њутн (Isaac Newton, 1643-1727) током 1694. године. Први је био најпре професор математике у Единбургу, а касније професор астрономије на Универзитету у Оксфорду, а други професор математике на Универзитету у Kембриџу. Према историчарима математике и расположивим документима, дискусије су се водиле приликом њихових сусрета у Kембриџу или Оксфорду. Поменути проблем и њима слични привукли су пажњу великог броја чувених математичара, као што су Дирихле, Гаус, Ермит, Лагранж, Минковски, а и многи у данашње време.
Проблем је чувен из више разлога: 1) формулација је не само елегантна, геометријски атрактивна, већ и врло једноставна; 2) упркос једноставне поставке, било је потребно 250 година да се дође до решења. Славни математичар Давид Хилберт једном приликом је рекао да је први критеријум за добар математички проблем тај да се он може с лакоћом објаснити „првој особи коју сретнете на улици”. Можда ово није квалификација универзалног типа, али се испоставило да неки од најчувенијих математичких проблема заиста задовољавају Хилбертов критеријум, као што су Фермаова последња теорема (доказана после 360 година), проблем четири боје (решен после 116 година), Kеплеров проблем оптималног паковања сфера (решен после скоро 400 година), Голдбахов проблем о простим бројевима (још није решен). Овим проблемима, свакако, треба придодати Грегори-Њутнов проблем додирујућих сфера.

Сл. 1 Оксфордска дискусија Д. Грегорија и
И. Њутна (Фото и дизајн В. Петковић)
Дејвид Грегори био је нећак чувенијег математичара Џејмса Грегорија (James Gregory, 1638-1675). Постао је професор математике у својој 24. години на Универзитету у Единбургу где је предавао Њутнове теорије. Дејвид Грегори је јако подржавао Њутна у историјској расправи с Лајбницом у вези с приоритетом у открићу интегралног и диференцијалног рачуна. С друге стране, Њутн је много помогао Дејвиду Грегорију да оствари успешну каријеру.
Проблем додирујућих сфера произашао је као резултат чувене дискусије између Дејвида Грегорија и Исака Њутна 1694. године: Kолико највише јединичних сфера може истовремено додиривати дату сферу исте величине?
Њутн је сматрао да је максималан број 12 сфера, док је Грегори веровао да је тачан одговор 13. Међутим, ниједан није имао доказ за своје тврђење, тако да су њихови одговори били само нагађања. Чија интуиција је била боља, сазнало се 250 година касније. Захваљујући овој дискусији поменути проблем се у литератури често назива Грегори-Њутновим проблемом.
Нека k(n) означава максималан број n-димензионалних сфера које додирују дату сферу у n-димензионалном простору, при чему су све сфере једнаке величине. Тада је, очигледно, k(1)=2 и k(2)=6, као што је приказано на слици 2.
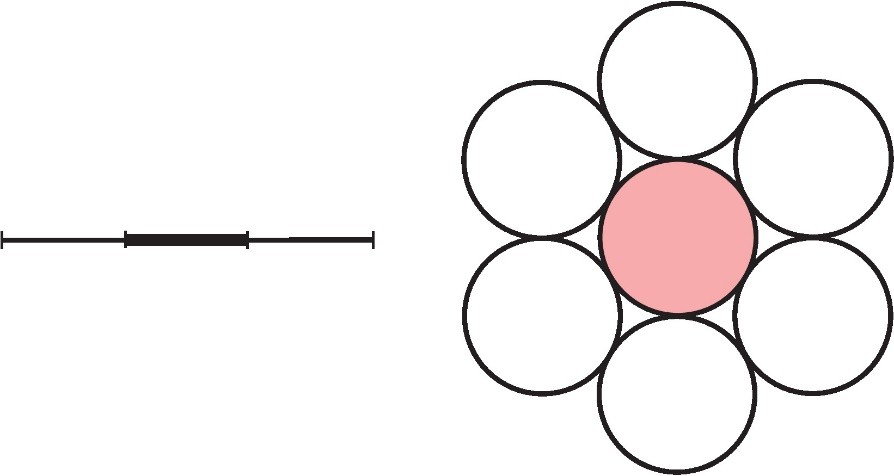
Сл. 2 Додирујуће сфере у једно и дводимензионалном простору
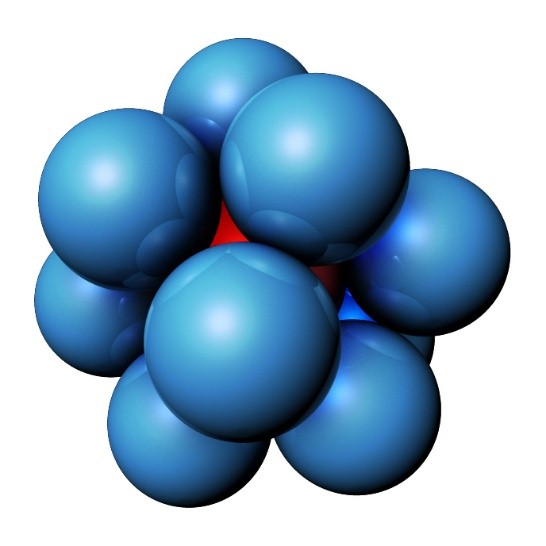
Сл. 3 Додирујуће сфере у тродимензионалном простору
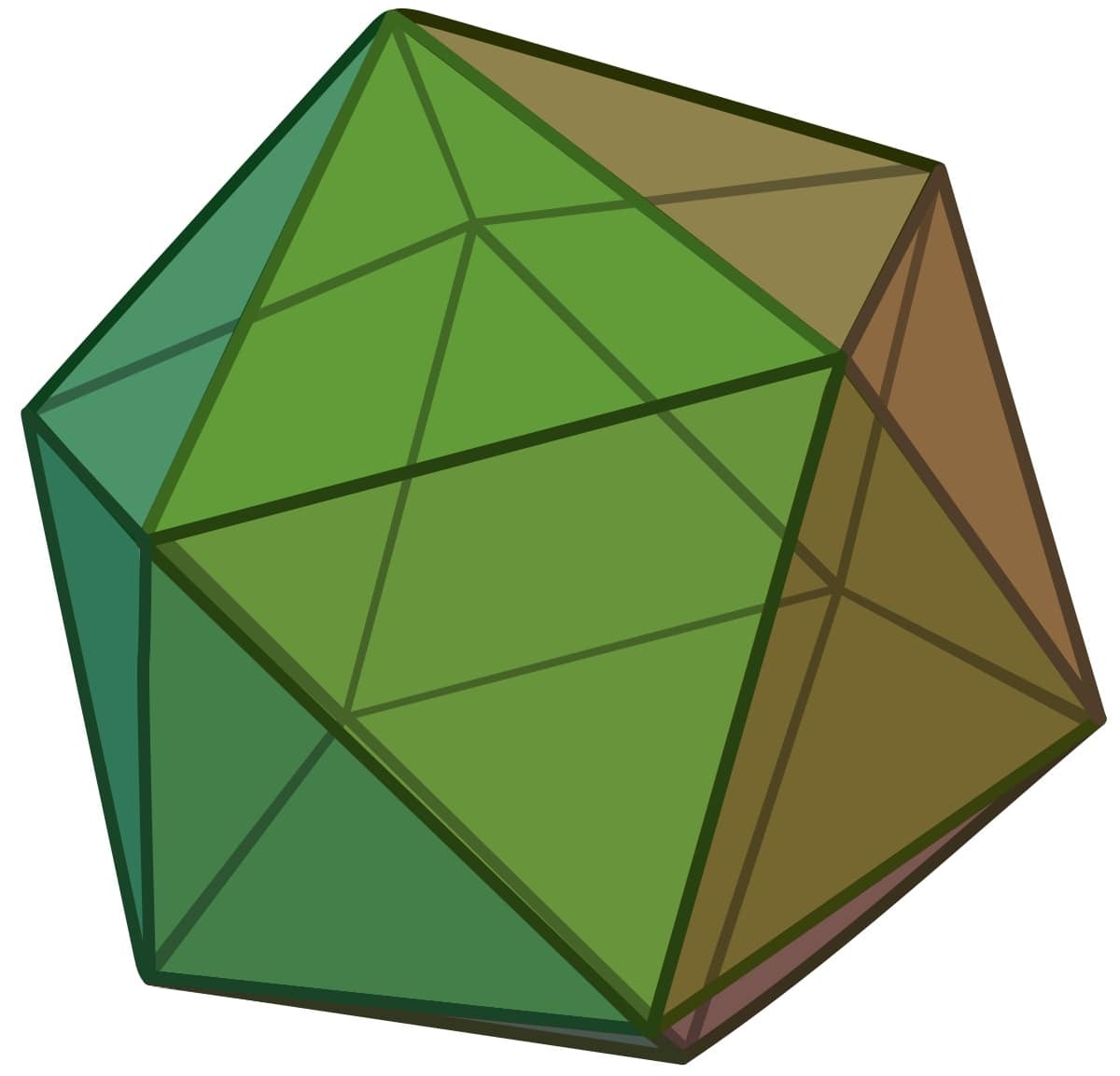
Сл. 4 Икосаедар
У тродимензионалном простору могуће је распоредити 12 сфера, тако да додирују дату сферу; на пример, додирујуће сфере могу се распоредити у теменима правилног икосаедра (икосаедар је правилни полиедар чије су стране једнакостранични троуглови (укупно 20) и има 12 темена и 30 ивица), што се може видети на слици 4. Дејвид Грегори и многи други аутори после њега сматрали су да ова конфигурација (као и неке друге конфигурације) оставља „доста простора” за тринаесту сферу. Дакле, k(3)=12 или k(3)=13, који је одговор тачан?
Више од 250 година овај проблем је остао нерешен, мада је било дато неколико „решења” у радовима и књигама из физике. Kоначно, проблем су дефинитивно решили Kурт Шитле и Бартел Л. ван дер Варден 1953. године.
Теорема. Не више од 12 јединичних сфера може се истовремено распоредити на такав начин да свака додирује дату сферу исте величине.
Другим речима, к(3)=12. Ово значи да је Њутнова интуиција била исправна мада за то није имао доказ. Три године после Шитлеа и Ван дер Вардена, Џон Лич дао је једноставно решење, разумљиво релативно широком кругу читалаца; довољно је познавање неких основних елемената из сферне геометрије и теорије графова. Његов доказ је садржао неке ситне некоректности, које су касније други аутори исправили. Заинтересовани читаоци могу наћи релативно једноставно и кратко решење руског математичара Олега Мусина (који живи у Лос Анђелесу) на линку https://arxiv.org/pdf/math/0410324.pdf
Да ли је могуће наћи k(n) за неко n > 3 у n-димензионалном простору? Прилично је изненађујуће да је проблем додирујућих сфера решен за врло високе димензије 8 и 24; нађено је k(8)=240 i k(24)=196560 (Ендру Одлиско, Нејл Слоун и Владимир Левенштајн, сви 1979.), али је проблем дуго остао отворен за димензију 4. Kоначно, већ поменути математичар Олег Мусин показао је 2004. године да је највећи број додирујућих сфера за димензију n=4 једнак 24.
У доњој табели дате су досад пронађене вредности за k(n).
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
24 |
|
k(n) |
2 |
6 |
12 |
24 |
40 |
72 |
126 |
240 |
196560 |