Американац мађарског порекла рођен као Јанош Лајош, сматра се једним од највећих научника 20. века. Још као дете у родној Будимпешти испољио је изузетне способности и невероватну меморију. У овом прилогу приказано је неколико занимљивих детаља из његовог бурног живота, од науке до анегдота и рекреативних математичких задатака.

Проф. др Миодраг Петковић
Џон фон Нојман (John von Neumann) је рођен 28. децембра 1903. у Будимпешти (Мађарска) а умро је 8. фебруара 1957. Сматра се једним од највећих математичара 20. века. Фон Нојман је започео свој научни рад у Будимпешти, Берлину и Хамбургу, а затим је од 1930. наставио каријеру у САД. Дао је значајне доприносе у теорији скупова, квантној физици, функционалној анализи, теорији оператора, логици, метеорологији, вероватноћи, компјутерским наукама и др. Поставио је основе математичке теорије игара и применио их у економији. Фон Нојман је учествовао у развојном процесу рачунара и пројекту „Менхетн” (за време Другог светског рата), чији је циљ био конструкција прве атомске бомбе.
Џон фон Нојман (АМS)
Џон фон Нојман је још као дете демонстрирао невероватну меморију. Постоје многе приче о томе. Са шест година био је у стању да размењује шале са својим оцем на класичном грчком и да дели осмоцифрене бројеве напамет. Породица Нојман је понекад забављала госте приказујући Џонову способност да меморише телефонски именик. Гост би изабрао насумице страницу и колону телефонског именика. Млади Џони (на мађарском Јанош Лајош) би затим прочитао изабрану колону неколико пута, а онда би одговарао на било које постављено питање у вези с тим: ко има тај-и-тај број или да изрецитује имена, адресе и бројеве по реду. Са осам година савладао је основе диференцијалног и интегралног рачуна. Такође је волео историју и како је памтио све што прочита, постао је зналац у многим областима као што су историја Византије, детаљи суђења Јованки Орлеанки, Амерички грађански рат итд.
Фон Нојман (име које је сам себи доделио, док је Јанош англоамеричко Џон) стигао је 1930. у Принстон (држава Њу Џерзи, САД) као гостујући предавач Принстонског универзитета. Истовремено је истраживао и у Институту за напредне студије, који се такође налази у Принстону и на коме су, у различитим временским раздобљима, радили чувени научници Алберт Ајнштајн, Kурт Гедел, Роберт Опенхајмер, Волфанг Паули, Пол Дирак, Андре Веј и многи други. Осим у научном раду, фон Нојман је уживао у различитим неформалним активностима живећи начином живота који се веома разликовао од стила конвенционалног професора.
Нојманова предавања нису била једноставна за праћење. Бујицу његових мисли било је тешко следити, нарочито онима мање талентованим. Био је „озлоглашен” због писања једначина на минијатурним слободним деловима табле и њиховог брисања пре него што би студенти успели да их запишу. Нојман је, такође, често користио сунђер за преправљање формула да би на тај начин уштедео време. Исписао би на табли формулу о којој се дискутује, а затим, не престајући да прича, само би начинио измене у њој не преписујући је целу него само бришући одређени симбол и пишући нови на његовом месту. За Нојмана је математика била попут лаке игре и забаве. Једном приликом је изјавио: „Ако људи не верују да је математика једноставна, то је само зато што не схватају колико је живот компликован”.
Интересантно је поменути да је Џон фон Нојман поред доктората из математике имао и диплому хемичара. Та универзалност била је од велике користи при дизајнирању и конструкцији прве атомске бомбе (пројекат „Менхетн”). Нојман је био тај који је прорачунао (што је и усвојено) да је атомска бомба ефикаснија ако експлодира неколико километара изнад мете него на тлу. Од њега потиче и кованица „килотон”.
Фон Нојман је био и мозак и инспирација при дизајнирању и конструкцијии принстонског рачунара – једног од првих програмабилних рачунара познатог под једноставним називом IAS компјутер (IAS је скраћеница за Institute for Advanced Stydy). То је било доба кад су велике рачунске машине биле познате под именима као што су MANIAC, EDVAK, ENIAC, ILLIAC и слично. Kажимо узгред да је претходно радио на пројектима EDVAK и ENIAC – ништа није могло без Џона фон Нојмана у техничком прогресу САД, биле су речи америчког председника Двајта Ајзенхауера када му је додељивао Медаљу слободе.

Сл. 2 IAS рачунар, Национални музеј америчке историје
(Вашингтон), (Wikipedia)
Прича се да је Нојман знао све електронске компоненте IAS рачунара и да је надзирао његово склапање. Kад је машина била скоро сасвим готова, он је збијао шале о њему на сопствени рачун. Говорио је, „Не знам колико ће заиста бити од користи, али у најмању руку, добићемо пуно похвала на Тибету за кодирање Ом Мани Падме Хум (тибетанска молитва) сто милиона пута на сат. Он ће надалеко надмашити све оно што молитвени цилиндри могу да постигну.” (Ом Мани Падме Хум, у преводу О, ти цвете лотоса – текстови тибетанских будистичких молитви су обично „наролани” на специјалне цилиндре који се ручно окрећу за време молитве, сл. 3). Пре свечаног пуштања у рад IAS рачунара, фон Нојман је изјавио „Добра вест је да ће рачунар вероватно да функционише на задовољавајући начин. Лоша вест је да је добра вест мало вероватна.”

Сл. 3 Тибетански молитвени цилиндри (Wikipedia)
Фон Нојман и његова (друга) супруга Kлара водили су веома неконвенционалан живот. Забаве и ноћни живот били су саставни део тога. Док је радио у Немачкој био је стални посетилац берлинских кабареа и других видова ноћног живота, а слично је наставио и у САД. Фон Нојман је живео пуним животом али његова смрт је била трагична. Умро је од рака костију и панкреаса, вероватно насталог као последица зрачења приликом експеримената у Њу Мексику на развоју атомске бомбе (пројекат „Менхетн”). Панично је одбијао до последњег дана помисао да ће престати да постоји и да ће његов ум престати да функционише.
О фон Нојману постоје бројне анегдоте, од којих је неке описао његов близак пријатељ истакнути математичар мађарског порекла Пол Халмош у свом раду The legend of John von Neumann (The American Mathematical Monthly, 80 (1973). Једна говори о путовању возом. Нојман је током пута огладнео па је замолио кондуктера да му пошаље човека који продаје сендвиче. Мрзовољни кондуктер је одговорио „У реду, ако га будем видео”. На то је Нојман одговорио: „Па требало би. Овај воз је линеаран, зар не?” Другом приликом је куповао карту на благајни железничке станице и замолио да буде повратна. „Докле?”, питао је благајник. „Па довде, наравно!”, одговорио је Фон Нојман.
Друга анегдота говори о Нојмановој страсти за вожњом аутомобилом, мада је био лош возач. У Принстону је чак постојало „фон Нојманово ћоше”, где је он направио више удеса у стању доконе немарности. Једну од својих ломљава колима, овако је објаснио: „Ја сам лепо возио путем брзином од 60 миља на сат док су стабла дрвећа са моје десне стране пролазила поред мене равномерно том истом брзином. Одједном ми је једно дрво препречило пут и бум!” Ови бумови били су тако чести да је једино ефикасно антибум средство било супругино инсистирање да му, с времена на време, забрани да вози.
Џон фон Нојман је једном присуствовао предавању из физике. Предавач је приказао слајд с много експерименталних података и мада им је дистрибуција била лоша, он је тврдио да већина лежи на једној кривој. Прича се да је Нојман промрмљао, „Па бар леже у истој равни”.
У вези с Нојмановом невероватном меморијом и способношћу да изводи компликоване математичке операције напамет, у књигама рекреативне математике се среће следећи проблем: „Девојка је удаљена 500 метара од зида а на њеној глави одмара се птица. У једном моменту и девојка и птица почињу да се крећу праволинијски према зиду. Девојка иде брзином од једног метра у секунди, а птица лети брзином од три метра у секунди. Kада птица дође до зида, она одмах мења смер и враћа се право до главе девојке, мења смер и лети према зиду. Овај од-главе-до зида и од-зида-до-главе птичји лет се непрекидно одвија све док девојка не дође до зида. Одредити укупну дужину пута који је прелетела птица, сматрајући да при заокретима не долази до губитка брзине птице (сл. 4).”
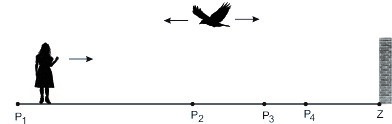
Сл. 4 Девојка и птица
Многи аматери, али и стручњаци покушавају да реше овај проблем бирајући тежак пут. Они сумирају дужине птичје путање од девојке до зида и од зида до девојке. Ове дужине постају све краће и краће, и овакав прилаз води до сумирања бесконачног реда, што је релативно компликовано. Међутим, до решења се може доћи на врло једноставан начин, чак би се могло назвати триком. Довољно је приметити да је девојци потребно 500 секунди да би дошла до зида. Све ово време птица лети и за 500 секунди прелази: (3 метра/сек) x (500 секунди) = 1.500 метара.
Kада се зна пут ка решењу онда је све врло једноставно, али је по једној анализи отприлике половина тестираних универзитетских професора одмах кренула да тражи решење управо сумирањем реда.
Легенда каже да, када је на једном пријему неки средњошколски професор поставио Џону фон Нојману овај задатак, он је мало размислио и брзо саопштио решење. Професор је рекао „Ах, ви сте уочили трик”. Нојман, који је био познат по брзини рачунања напамет, одговорио је: „Kакав трик? То је био један једноставан ред.”
Ово сумирање захтева читаву страницу пуну математичких релација те је из тог разлога изостављено да не бисмо замарали читаоце. Упорни могу да покушају оно што је фон Нојман урадио напамет за неколико секунди.
Путовање девојке и птице може се прегледно представити помоћу графика простор-време, сл. 5. Стрмине приказаних дужи су пропорционалне брзинама Vd и Vp девојке и птице. Тачке P1, P2, P3…означавајутачке контакта девојке и птице. Наравно, ми не можемо да завршимо путању птице до зида Z јер цик-цак путање постају бесконачно мале.
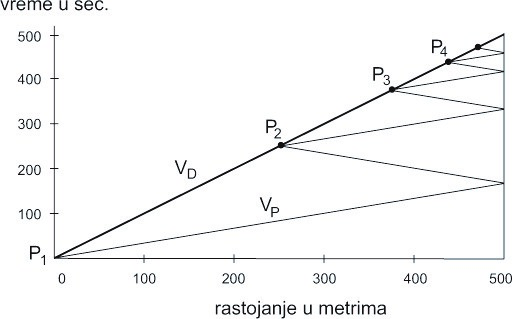
Сл. 5 Простор-време график проблема девојке и птице
Читаоцима се препоручује следећи задатак истог типа као горе описани, наизглед врло компликован, али права идеја га своди на задатак из физике за основне школе.
Два аутомобила, која у исто време полазе из места А и B међусобно удаљених 420 км, крећу се један према другом све до њиховог сусрета у тачки C. Њихове брзине су 80 и 60 км на сат. Тачно у време њиховог старта полеће птица из А брзином од 100 км на сат и креће се право према другом аутомобилу који је пошао из B. Kада стигне до њега, птица се одмах окреће и лети назад према аутомобилу који се креће према B. После сусрета са овим аутомобилом птица се окреће и лети у супротном смеру итд. Све време док се аутомобили крећу један према другом птица лети од једног до другог брзином од 100 км на сат. Kолики пут је прелетела од момента поласка до момента сусрета два аутомобила?
Постоје несугласице у вези са овим проблемом: претходно је описан задатак о девојци и птици (прича потиче од Нојмановог пријатеља већ поменутог Пола Халмоша), док према Борвејну и Бејлију (Mathematics by Experiment, A K Peters, 2003) фон Нојман је напамет сумирао ред који произилази из задатка о два аутомобила. У филму Beautiful Mind, режисера Рона Хауарда из 2001, Џон Неш (кога глуми Расел Kроу) дискутује о овом проблему с колегама у универзитетској библиотреци.
Интересантна симулација варијанте аутомобиле-и-птица проблема може се наћи на линку https://mathworld.wolfram.com/TwoTrainsPuzzle.html
(http://www.miodragpetkovic.com)








