Иако је био један од највећих светских аутора математичких и логичких загонетки, ребуса, шаховских проблема и занимљивих играчака (звали су га „Kраљ загонетки”), имао је поприличну ману – присвајао је загонетке других аутора и објављивао их под својим именом, што му је најчешће и успевало јер је био првокласан манипулатор и менаџер.

Проф. др Миодраг Петковић
Повремено ће се у овој рубрици у појављивати занимљиви прилози из света математике који укључују интересантне математичке формуле, догађаје из света математике и живота великих математичара, као и елементарне али интригантне и изазовне задатке за чије решавање је довољно средњошколско знање математике. Већина ових прилога, као и још математичких прича и занимљивости може се наћи на сајту аутора ових прилога, опција теме:
Kрајем 19. века Лојдова „слагалица-15”, Aмериканца Семјуела Лојда (1841-1911), изазвала је праву светску хистерију. Слагалица има 15 квадратних плочица и једно празно место на плочи димензије 4×4. Ове плочице су смештене у кутији тако да се не могу вадити, али се могу померати хоризонтално и вертикално. На почетку, плочице су поређане као на слици 1, редом од 1 до 13, затим 15 па 14.
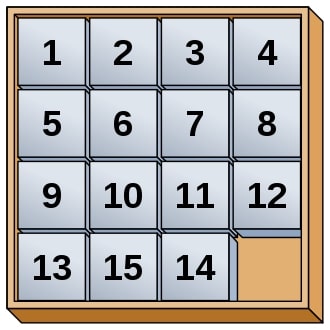
Сл. 1 Лојдова слагалица с 15 бројева
Треба рећи да Семјуел (Сем) Лојд није креатор слагалице већ Нојес Чепман који је лансирао ову загонетку 1880. Године 1891. Сем Лојд је објавио слагалицу под својим именом и тако је остало и до данас. Иако је био један од највећих светских аутора математичких и логичких загонетки, ребуса, шаховских проблема и занимљивих играчака (звали су га „Kраљ загонетки”), имао је поприличну ману – присвајао је загонетке других аутора и објављивао их под својим именом, што му је најчешће и успевало јер је био првокласан манипулатор и менаџер.
Kод слагалице-15 задатак се састоји у томе да се квадратне плочице померају горе, доле, десно и лево, користећи празан квадрат, све док се бројеви не поставе у строго растућем поретку 1, 2…14, 15. Прича се да је Сем Лојд понудио 1.000 долара за тачно решење (данас би то било око 30.000 долара). Одмах да кажемо да је Лојд, као добар математичар, знао да из ове почетне позиције загонетка нема решење тако да је и могао да буде тако дарежљив.
Интересантна је прича о Лојдовом покушају да патентира ову слагалицу.
Kада га је службеник pатентног уреда замолио да демонстрира решење, Лојд је одговорио да то није могуће (наравно, реч је о почетној позицији 15-14 која се налазила у кутијама). „Наш завод прихвата патенте само оних ствари које раде, овде то није случај”, одговорио је службеник и одбио захтев. Слагалица се и дан-данас може набавити у радњама са играчкама и то у разним варијантама (често и као слагалица-мозаик уместо бројева).
Читаоце сигурно занима под којим условима је могуће решити Лојдову слагалицу. Постоје почетне позиције за које је могуће решити слагалицу, док за друге почетне позиције то није могуће, и то у односу отприлике пола-пола. Ова чињеница је веома импресионирала математичаре током деценија, и они су се дали на посао да математичким путем одреде када је слагалицу могуће решити, а када не.
Пре него што дамо услове под којима је могуће решити слагалицу-15, подсетимо се неких најосновнијих особина из области математике која се назива комбинаторика. Посматрајмо скуп S={a,b,c} од 3 елемента. Тада се под пермутацијом без понављања реда 3 подразумевају сви распореди (1,2,3), (1,3,2), (2,1,3), (2,3,1), (3,1,2), (3,2,1). Дужина пермутације може бити и мања од укупног броја елемената скупа S, на пример, ако је дужина 2 тада имамо следеће пермутације реда 2: (1,2), (2,1), (1,3), (3,1), (2,3), (3,2).
Важан појам у комбинаторици јесте инверзија пермутације: уређен пар елемента {Pi,Pj} (код кога се зна који елемент је на првој, а који на другој позицији) назива се инверзијом у пермутацији P ако се Pi јавља пре Pi, а притом је Pi > Pj. На пример, пермутација (3,1,4,5,2) има 4 инверзије (3,1), (3,2), (4,2) и (5,2).
Укупан број инверзија I(P) у пермутацији P добија се као сума елемената вектора пермутационих инверзија. Број инверзија у пермутацији је једнак броју размена суседних елемената неопходних за добијање њиховог природног уређења. Приметимо да у правоугаоној слагалици било које димензије m x n која има један празан квадрат, свако померање једне плочице мења број инверзија у пермутацији за два; паран број остаје паран а непаран остаје непаран.
У случају Лојдове слагалице-15 {P1,P2…P15} нека је i редни број квадата слагалице рачунајући почев од првог елемента прве врсте и идући с лева на десно, врсту по врсту. Ако је број Pi већи од Ni бројева који се јављају после броја Pi, кажемо да је ред његове инверзије једнак Ni. Укупан број инверзија једнак је
I(P) = N1 + N2 +… + N15 = N2 +… + N15,
при чему се сабирање може вршити од 2 до 15 јер је увек N1 = 0 с обyиром да не постоје природни бројеви мањи од 1.
За оне који нису довољно упознати са термином пермутација, појаснићемо горње излагање на следећем примеру почетне позиције у слагалици-15 представљене преко квадратних шема 4 x 4 броа, слика лево. На слици десно је број инверзија за одговарајући број из шеме на левој страни. На пример, за број 7 (лево) број инверзија је 4 јер се 7 јавља испред бројева 4, 8, 1, 12, 14, 9, 3, 15, 2, али је већи само од 4, 1, 3 и 2.
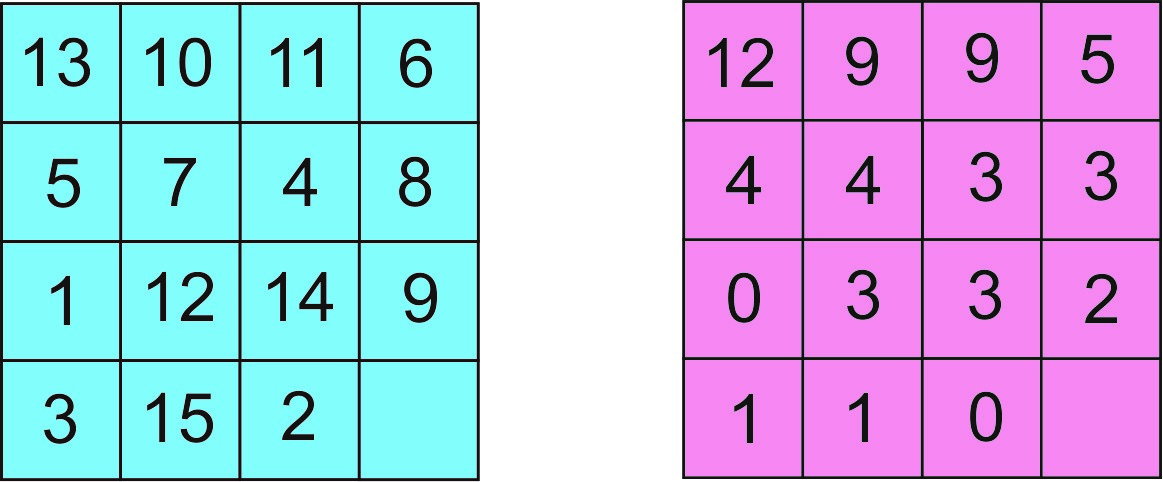
Из шеме инверзија (десно) налазимо да је укупан број инверзија I(P) = 59.
Математичари су брзо дошли до услова за решивост слагалице 15:
Ако је укупан број инверзија I(P) који се односи на почетну позицију паран, решење слагалице-15 постоји; ако је овај број непаран, решење не постоји.
На основу овог услова решивости следи да је последњи пример слагалице нерешив јер је укупан број инверзија 59 непаран број. У случају Лојдове загонетке са замењеним местима бројевима 14 и 15 (слика 1) имамо да је N14 = 1, док за све остале важи Ni = 0 Према томе, I(P) = 1 дакле непаран број, тако да се из почетне позиције коју је задао Лојд постављање бројева у растући низ од 1 до 15 не може постићи.
Немачки математичар В. Аренс описао је атмосферу у Европи насталу после појаве Лојдове слагалице: „Kрајем деветнаестог века слагалица ,петнаест’ појавила се у САД и врло брзо се проширила захваљујући огромном броју играча које је освојила изазвавши велике невоље. Иста ствар се десила и у Европи. У канцеларијама и продавницама послодавци су били ужаснути понашањем запослених који су играли игру за време радног времена и школских часова. Чак су се и озбиљни и времешни посланици за време заседања немачког Рајхстага (парламента) забављали овом слагалицом. Власници радњи су заборављали да ујутру отворе своје радње, возови су каснили, бродови су ударали у докове, уважена господа су у касним вечерњим сатима испод уличних лампи решавала слагалицу. На улицима су се пролазници сударали обузети премештањем плочица, играло се по парковима и трамвајима. (Да подсетимо, нешто слично се десило и сто година касније саРубиковом коцком и игром ,тетрис’). Из Париза игра се брзо проширила из главног града на све провинције. Један француски новинар је писао да је скоро свака сеоска кућа у провинцији имала ову слагалицу и читава домаћинства су заборављала (или одлагала) пољопривредне радове да би решавали Лојдову слагалицу.”
Разлог за ову хистерију је лако објаснити; игра је довољно једноставна тако да је могао да је игра свако, жеља за успехом била је огромна (у то време нудиле су се и награде за успешно решење), а хистерија је предуго трајала јер слагалица са почетном позицијом није могла да се сложи како је захтевано.
Интересантно је напоменути да је чувени шахиста и бивши светски првак Боби Фишер био експерт за решавање ове загонетке-играчке; он је био у стању да реши слагалицу за мање од 30 секунди из било које решиве почетне позиције.
Од интереса је поменути да Семјуела Лојда сматрају једним од највећих састављача математичких и логичких загонетки, шаховских проблема и ребуса. Не само аматери, већ и универзитетски професори су дане и недеље проводили у решевању његових главоломки. Због тога аутор овог прилога сматра да је он, осим слагалице, заслужио да се помену још две његове чувене загонетке.
Прва од њих је математичко-логичког карактера, опште позната под именом Анамарија проблем, и гласи овако: Ана и Марија имају заједно 44 године. Марија је два пута толико стара колико је Ана била када је Марија била упола толико стара колико ће Ана бити када Ана буде три пута толико стара колико је Марија била када је Марија била три пута толико стара колико је тада била Ана.
По колико година имају Ана и Марија? За решавање овог проблема довољно је знање из основне школе, наравно уз добру идеју.
Решење: Нека је M број Маријиних година, а A Аниних. Даље, нека је пре X година „… Марија била два пута толико стара колико је Ана била…”, а да ће кроз Y година „… колико ће Ана бити…”, и да је пре Z година „… Марија била три пута толико стара колико је тада била Ана”. На основу овог имамо следећи систем од пет једначина:
M + A = 44
M = 2(A-X)
A + Y = 2(M-X)
A + Y = 3(M-Z)
M – Z = 3(A-Z).
Решавањем горњег система налазимо да је М=27,5 и А=16,5. Дакле, Марија има 27 и по, а Ана 16 и по година.
Сем Лојд се сматра и једним од највећих састављача шаховских проблема свих времена. Експерти који прате ову посебно врсту задатака су сагласни да је он унео у шаховску композицију скоро све важне идеје, мотиве и теме, и то пре 150 година. За љубитеље ове врсте задатака, који су деценијама (а и данас) били саставни део скоро свих дневних новина и недељника, ево једног интересантног шаховског проблема. Бели игра први и најдаље у свом трећег потезу матира црног. Решење изостављамо да не бисмо кварили ужитак читалаца при решавању овог чувеног проблема.
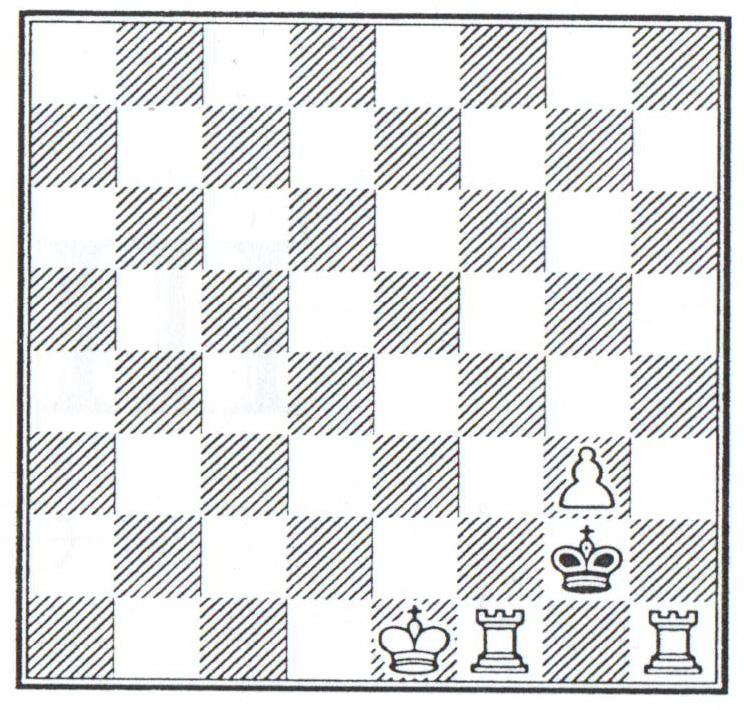









Putem imejla (dostupan preko mog sajta) nekoliko čitalaca zamolilo me za rešenje Lojdovog šahovskog problema – mat u 3 poteza. Evo rešenja:
Označimo vertikale šahovske table slovima a,b,c,d,e,f,g,h a horizontale brojevima od 1 do 8 (standardna šahovska notacija). U prvom potezu beli igra 1. Tf4. Ako crni kralj uzme topa na h1, beli igra kraljem 2. Kf2 i mat je neizbeżan topom na h4. Druga varijanta je mnogo interesantnija, zbog koje je problem i postao tako čuven. Ako crni kralj uzme pešaka na g3, beli vuče veoma domišljat potez: vrši malu rokada i crni će biti matiran u 3. potezu.
Postavlja se pitanje da li je Lojdova pozicija regularna? Naime, kako je crni kralj dosao na g2 s obzirom da beli kralj i ugaoni top na h1 nisu povukli nijedan potez (zbog kasnije rokade u resenju)?
Pitanje je sasvim na mestu, šahovski problem se smatra korektnim jedino ako je do postavljene pozicije moguće doći regularnim šahovskim potezima. Analiza korektnosti šahovskog problema pripada oblasti retrogradne analize, nekoj vrsti “šahovskog vremeplova.” Lojdov problem je korektan; jedna jednostavna pozicija iz koje se može doći je postavka u kojoj se crni kralj nalazi na polju h3, bilo koja crna figura na g3 i beli pešak na h2, dok su beli kralj i topovi na istim poljima kao na dijagramu. Beli uzima pešakom crnu figuru na g3 i topom daje šah a crni kralj dolazi na polje g2. I to je Lojdova pozicija data u prilogu. Alternativno, beli pešak može biti na polju f2, a crni kralj na f3.
I jedna ispravka tipo-greške u prilogu: umesto „… ako se Pi javlja pre Pi, a pritom je Pi > Pj“,
treba „…ako se Pi javlja pre Pj, a pritom je Pi > Pj“