Peterburški paradoks prvi je razmatrao Nikolaus Bernuli 1713. i aktuelan je i u današnje doba, specijalno za matematičare i ekonomiste koji se bave teorijom odlučivanja. Standardna verzija izvedena je iz igre iz Sankt Peterburga u kojoj igrač A (kazino u modernom dobu) i igrač B bacaju ispravan novćić („glava”/„pismo”) sve dok se ne pojavi pismo. Ako je n broj uzastopnog pojavljivanja glave, igrač A isplaćuje igraču B 2n-1 kruna.

Prof. dr Miodrag Petković
Koristeći osnovne elemente teorije verovatnoće proizilazi da je iznos u krunama koji bi igrač B realno mogao da očekuje (jednak matematičkom očekivanju) beskonačno veliki! Koliko novca igrač B bi trebalo da uloži da bi igrao ovu igru? Paradoks proizilazi iz protivrečnost između onog iznosa koji je igrač B spreman da plati da bi igrao ovu lutrijsku igru i (teorijski) beskonačnog iznosa koji očekuje.
Mnogi matematičari iz 18. i 19. veka bavili su se problemom poznatim kao Peterburški paradoks. Problem je formulisao švajcarski matematičar Nikolas Bernuli (1687-1759) u pismu Pjeru Rejmonu de Monmoru 9. septembra 1713. godine. Međutim, paradoks je dobio ime po analizi koju je razradio Nikolasov rođak Danijel Bernuli (1743-1794) koji je jedan deo života proveo u ruskom gradu Sankt Peterburgu. On je svoju analizu objavio 1738. godine u časopisu Commentarii Peterburške akademije. Paradoks se odnosi na matematičko očekivanja pri lutrijskoj igri bacanja novčića.
Dvojica igrača A (recimo kazino) i B igraju igru pod sledećim uslovima: Pri bacanju ispravnog novčića (glava/pismo) igrač A vrši isplatu igraču B pri svakom bacanju kada padne „glava”. Igra se završava kada se prvi put pojavi „pismo”. Ako se glava pojavi u prvom bacanju, A plaća igraču B jednu krunu; ako se pojavi u drugom bacanju, A isplaćuje dve krune; ako se pojavi u trećem, četiri krune i tako dalje, udvostručavajući sumu svaki put. Konačno, ako se glava pojavi u n-tom bacanju, igrač B dobija 2n-1 kruna od igrača A. Pretpostavka je da se igra može nastaviti beskonačno. Koliki iznos može da očekuje igrač B?
Pitanje se može formulisati i ovako: „Koliko novca bi igrač B trebalo da uloži da bi igrao ovu igru”?
Verovatnoća da igrač B dobije jednu krunu iznosi 1/2, da dobije dve krune 1/4 i tako dalje. Dakle, ukupan broj kruna koji bi igrač B realno mogao da očekuje (jednako matematičkom očekivanju) iznosi
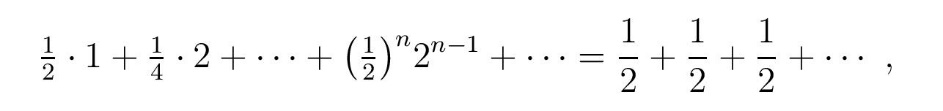
što daje beskonačan zbir! Neki autori opisuju da se u ovoj igri na sreću zbir približava beskonačnosti, a ne da je beskonačan uzimajući u obzir realnu situaciju da nije moguće fizički obaviti beskonačan broj bacanja novčića.
Paradoks proizilazi iz protivrečnosti između onog iznosa koji je igrač B spreman da plati da bi igrao ovu lutrijsku igru i (teorijski) beskonačnog iznosa koji očekuje. R. Martin u knjizi The St. Petersburg Paradox” (The Stanford Encyclopedia of Philosophy, Stanford University, 2004) piše: „U strogo logičkom smislu, Peterburški paradoks nije paradoks jer se ne izvodi nikakva formalna kontradikcija. Međutim, tvrdnja da racionalni vlasnik kazina rizikuje (istina s vrlo malom verovatnoćom) da plati milione, čak milijarde, izgleda apsurdno”. Martin, takođe, navodi da bi samo mali broj igrača B platilo 25 dolara da uđe u ovu igru.
Još je Danijel Bernuli izjavio da, iako matematičko očekivanje zaista daje beskonačan iznos, igrač A (u modernom dobu kazino) bi rado startovao sa 20 dukata. Izvesno je da će igrač B osvojiti veoma skroman iznos. Objašnjenje je jednostavno: verovatnoća da igrač B ne osvoji više od 2 dolara je 1/2, a da ne osvoji više od 4 dolara je 3/4. Verovatnoća da pri bacanju novčića glava uzastopce padne (recimo) 10 puta iznosi 1/(210 )= 1/1024 ili oko 0,1%.
Ovaj neočekivan rezultat privukao je pažnju mnogih matematičara, uključujući braću Danijela i Nikolasa III Bernulija i veliku grupu francuskih matematičara. Žan le Ron Dalamber (Jean le Rond D’Alambert, 1717-1783), jedan od najvećih matematičara tog doba, pisao je Žozefu Luju Lagranžu, drugom slavnom francuskom matematičaru: „Vaša knjiga o igrama čini me veoma nestrpljivim da nam date rešenje Peterburškog problema, koji mi se čini nerešivim na osnovu poznatih principa”. Francuski matematičari Kondorse (Nicolaus Condorcet, 1743-1794) i Poason (Simèon Poisson, 1781-1840) smatrali su da igrač A ulazi u aranžman koji je za njega nepovoljan i da igra sadrži neke kontradikcije.
S druge strane, Žozef Bertran (Joseph Bertand, 1822-1900) je tvrdio da je ova teorija (i rezultat koji je gore dat) sasvim korektna i jedino uslovi igre daju prednost igraču B, što dovodi do neočekivanog rezultata. On je smatrao da, ako bi se broj bacanja ograničio, tada bi šanse dvojice igrača bile drugačije. Na primer, za sto bacanja igrač B bi morao da uloži 15 kruna da bi igrao (suma jednaka matematičkom očekivanju njegovog dobitka) i tada bi njegov rizik da izgubi bio veći. Uslovi igre bi i dalje favorizovali igrača B, što proističe iz mogućnosti velikog dobitka, mada je verovatnoća za to mala. Ulog igrača B zavisi od broja bacanja koje mora A da izvede. Ako je taj broj n, Bertran je izračunao da ulog igrača B treba da bude
![]()


Epitaf Nikolasu Bernuliju (1759), Portret Danijela Bernulija
(1725) (CC-BY-SA-4.0)
Neki matematičari ponudili su rešenje koje se zasniva na činjenici da je sreća igrača u praksi konačna pa, prema tome, njegov dobitak ne može biti neograničen. Grof De Bifon (De Buffon, 1707-1788) je, čak, izveo empirijski test kako bi pronašao prosečnu sumu. Danijel Bernuli je tragao za rešenjem preko svog principa moralnog očekivanja, u skladu s kojim je zamenio iznose
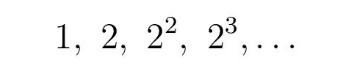
sa
![]()
Zapravo, on je smatrao da vrednost dobitka nije samo u broju osvojenih kruna, već se sastoji i od zadovoljstva usled dobitka. Prema njegovom rezonovanju, nastala sreća zbog dobitka od 100 miliona kruna neće se udvostručiti ako se dobije još 100 miliona. Uopšte, ako je a početni iznos a dodatni iznos b, koristeći svoj princip moralnog očekivanja Danijel Bernuli je porast sreće nastale usled dobitka dodatnog iznosa b izrazio integralom
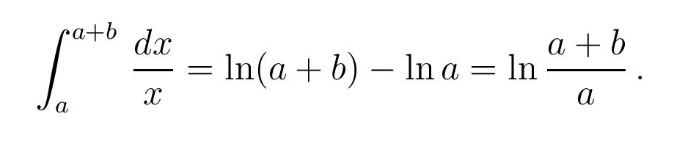
Na primer, u slučaju udvostručavanja nekog dobitka (sume novca ili broja nekih predmeta), uvećanje sreće po D. Bernuliju biće oko 70% a ne 100% jer je
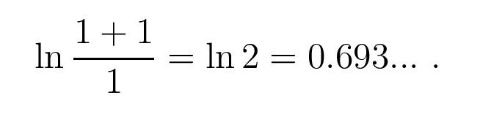
Pokušajte sebe da testirate: ako ste dobili novi automobil, a potom još jedan istih karakteristika, da li ćete biti dvostruko srećniji?


Sankt Peterburg (Pixabay)
Danijel Bernuli je Peterburški paradoks prokomentarisao sledećim rečima; „Određivanje vrednosti neke stvari ne sme biti zasnovano na ceni, već na korisnosti koju ona donosi… Nema sumnje da je dobitak od hiljadu dukata značajniji za siromaha nego za bogataša, iako i jedan i drugi dobijaju isti iznos”.
Među različitim pristupima da se problem modifikuje da bi se dobio konačan odgovor, jedan od najprihvatljivijih je predložio Gabrijel Kramer (oko 1730). Kramer je pošao od pretpostavke da igrač A poseduje ograničenu sumu novca, recimo 224=16.777.216 kruna. Tada postoji verovatnoća 1/(2n ) da će igrač B dobiti 2n-1 kruna u n-tom bacanju samo dok je n < 25; nakon toga on može dobiti samo 224 kruna. Kako je
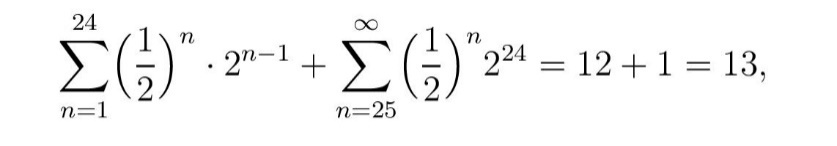
očekivanje igrača B je 13 kruna, što je razumna suma. Interesantno je pomenuti da bi u slučaju danas najbogatije osobe na svetu Ilona Maska (čije je bogatstvo u aprilu 2022. procenjeno na 265 milijardi dolara) ulog u igri Kramerovog tipa bio samo 20 (= 19 + 1) dolara jer je posle 38-og bacanja dobitak konstantan i iznosi „samo” 238 dolara (jednako Maskovom bogatstvu, 265 milijardi ≈ 238 ), ali je broj bacanja novčića teorijski beskonačan. U to se možemo lako uveriti ako broj 24 u prethodnoj formuli zamenimo brojem 38.
Postoje više varijanti Peterburškog paradoksa konstruisane uvođenjem raznih uslova u igri koji dovode do različitih ishoda, pri čemu se koriste raznovrsni alati i analize iz različitih disciplina, počev od ekonomije, filozofije, sociologije, verovatnoće, pa sve do Remzijeve teorije i psihologije (preciznije, ljudskog ponašanja u riskantnim situacijama koja donekle imaju veze sa popularnim kvizovima tipa „Kako postati milioner” ili ponašanjem brokera na berzi kada je u pitanju izbor između ponuđenih alternativa). Detalje u vezi Peterburškog paradoksa diskutovali su History of the Mathematical Theory of Probability, London, 1865), E. Kamke, Einführung in die Wahrscheinlichkeitstheorie, Leipzig, 1932), M. Kretik (Mathematical Recreation, New York, 1953), Rauz Bol i Kokseter (Mathematical Recreations and Essays, New York, 1987) i drugi.








