Logično je pretpostaviti da se kao prva cifra u dovoljno dugim listama numeričkih podataka podjednako pojavljuju cifre od 1 do 9. Međutim, još 1881. Simon Njukomb je primetio paradoksalnu pojavu da se broj 1 javlja kao prva cifra u skoro 30% razmatranih lista numeričkih podataka, dok se procenat javljanja ostalih cifara smanjuje sa rastom cifara od 1 do 9! Ovaj neočekivan fenomen prve cifre, koji je kasnije temeljno izučavao fizičar Frenk Benford, tema je ovog priloga.
Prof. dr Miodrag Petković
Koliko se često kao prva cifra u dovoljno dugim listama numeričkih podataka pojavljuju cifre od 1 do 9? Logično je očekivati da je frekvencija pojavljivanja ovih cifara približno ista. Međutim, najpre je matematičar i astronom Simon Njukomb primetio 1881, a zatim je fizičar Frenk Benford (General Electric Co.) u svom radu The Law of Anomalous Numbers iz 1938. objavio da se javlja neobična frekvencija cifara od 1 do 9 u listama numeričkih podataka, ne samo pri izvođenju eksperimenata u fizici i inženjerskim disciplinama, već i u geografskim podacima (npr. površine ostrva i država, dužine reka, broj stanovnika), berzanskim podacima, brojevima kuća u dužim ulicama itd. Broj 1 se javlja kao prva cifra u skoro 30% razmatranih slučajeva (u Benfordovom istraživanju bilo ih je 20.229), dok se procenat javljanja ostalih cifara smanjuje sa rastom cifara od 1 do 9! Najbolja provera se može zapaziti prelistavajući logaritamske tablice. Zbog toga se opisano ponašanje često naziva zakon prve cifre ili fenomen vodeće cifre.
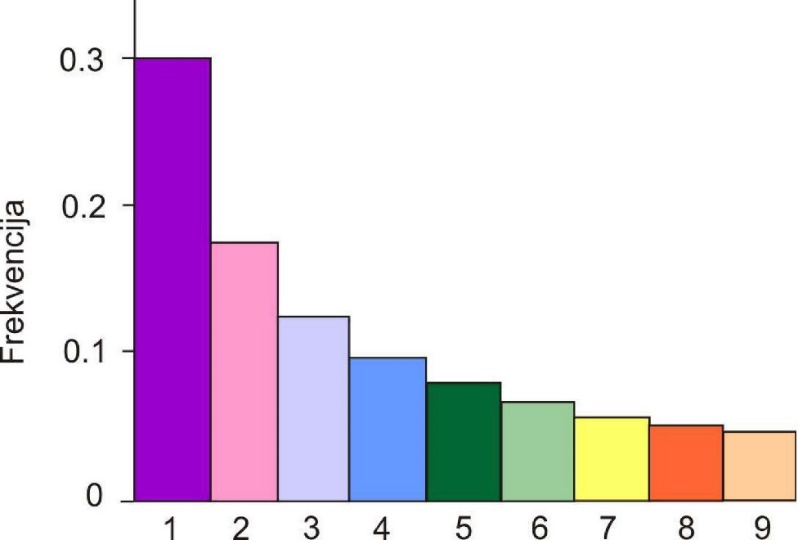
Sl. 1 Frekvencija pojavljivanja cifara kao vodeće cifre
Benford se posvetio ovom problemu i posle ispitivanja velikog broja numeričkih podataka različitog tipa došao je do empririjske formule za verovatnoću pojavljivanja P(n) cifre n kao prve cifre, koja glasi
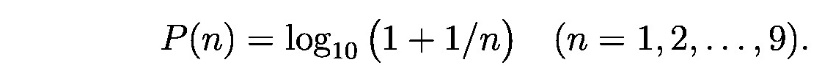
Ovaj zakon nazvan je Njukomb-Benfordov zakon, mada se u literaturi češće sreće naziv Benfordov zakon. Teorijske frekvencije (prema poslednjoj formuli) prikazane su grafički na slici 1, a numeričke vrednosti su date u tabeli 1 (videti, takođe, poslednju kolonu tabele 2).
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
P(n) |
30.1% |
17.6% |
12.5% |
9.7% |
7.9% |
6.7% |
5.8% |
5.1% |
4.6% |
Tabela 1 Teorijske frekvencijcije brojeva od 1 do 9 (u %)
Benfordov zakon se još naziva i „zakonom moći” ili „zakonom veličine”. Na primer, velika jezera su retka a mala znatno češća. Slično, u prvom intervalu 1-100 ima 11 Fibonačijevih brojeva, a u sledećim intervalima [101-200, [201-300] i [301-400] samo po jedan. Podsećamo da su prvi brojevi Fibonačijevog niza
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377…
Kod ovog niza svaki član, izuzev prva dva, jednak je zbiru dva prethodna člana. Evo još par sličnih primera: dobro poznati beskonačni nizovi, kao što su faktorijeli n! i stepeni broja 2 (ali i drugih brojeva) zadovoljavaju Benfordov zakon tačno ili asimptotski.
Kao dobra ilustracija može poslužiti i ulaganje u akcije neke kompanije. Jednostavnosti radi, neka je početna vrednost akcija 100 dolara i godišnja kamata 10%. Prva cifra je 1. Sledeće godine stanje na računu je 110 dolara, dakle 1 je ponovo vodeća cifra. Da bi se došlo do vrednosti akcija od 199 dolara potrebno je da prođe 88 meseci. Posle toga vrednost akcija se izražava brojevima koji počinju cifrom 2, od 200 do 299, i za to su potrebna 52 meseca. Cifra 9 javljaće se samo 12 meseci (vrednost akcija od 900 do 999).
Od interesa je sledeća primena Benfordovog zakona. Zasnovano na prihvatljivoj pretpostavci da su ljudi koji izmišljaju brojeve skloni da svoje cifre raspodeljuju prilično ravnomerno, osobe koje žele da krivotvore podatke pri prijavljivanju poreza ili sličnim prevarama, nastoje da u svojim prijavama upišu brojeve tako da se sve cifre javljaju približno podjednak broj puta. Ova prevara se detektuje primenom Benfordovog zakona prema kome se frekvencije pojavljivanja cifara razlikuju. Prema istraživanjima Hala Varijana sa Univerziteta Kalifornija u Berkliju, Benfordov zakon mogao bi se koristiti za otkrivanje mogućih prevara u socio-ekonomskim podacima koji se podnose u prilog odlukama u oblasti javnog planiranja.
Interesantan je primer u kome se posmatraju vodeće cifre visina 58 najviših zgrada na svetu, videti tabelu 2. Vodeće cifre visina zgrada ponašaju se približno po Benfordovom zakonu, i to nezavisno da li su visine izražene u metrima (m) ili stopama (ft).
5858
|
Vodeća cifra n |
m |
ft |
Po Benfordovom zakonu |
||
|
Broj zgrada sa vodećom cifrom visine n |
% |
Broj zgrada sa vodećom cifrom visine n |
% |
||
| 1 | 24 | 41.4 % | 16 | 27.6 % | 30.1 % |
| 2 | 9 | 15.5 % | 8 | 13.8 % | 17.6 % |
| 3 | 7 | 12.1 % | 5 | 8.6 % | 12.5 % |
| 4 | 6 | 10.3 % | 7 | 12.1 % | 9.7 % |
| 5 | 1 | 1.7 % | 10 | 17.2 % | 7.9 % |
| 6 | 5 | 8.6 % | 4 | 6.9 % | 6.7 % |
| 7 | 1 | 1.7 % | 2 | 3.4 % | 5.8 % |
| 8 | 4 | 6.9 % | 5 | 8.6 % | 5.1 % |
| 9 | 1 | 1.7 % | 1 | 1.7 % | 4.6 % |
| 58 | 58 | ||||
Tabela 2 Vodeće cifre visina najviših zgrada na svetu (Wikipedia)
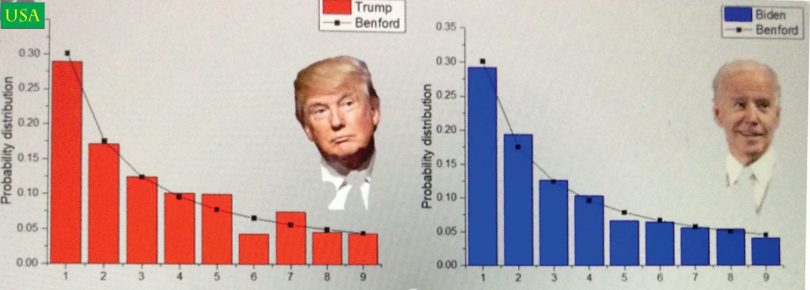
Francuz Budevin Rukema je samo nekoliko dana posle osporavanih parlamentarnih izbora juna 2009. godine u Iranu obavio istraživanje na osnovu frekvencije vodećih cifara u brojevima koji predstavljaju rezultate izbora po raznim regionima i zaključio da je broj glasova u izborima za predsednika korigovan naviše. S druge strane, odstupanja podataka sa predsedničkih izbora u SAD 2020. od onih dobijenih pomoću Benfordovog zakona bila su minimalna, što se može videti iz naslovne ilustracije ovog priloga. Ipak, istraživanja na Kolumbija univerzitetu poslednjih godina pokazala su da primena Bedfordovog zakona za otkrivanje prevara na izborima nije dovoljno verodostojna ukoliko postoji veliki broj izbornih jedinica koje imaju mali broj glasača.
Navedimo jednu interesantnu i korisnu primenu Benfordovog zakona: odnedavno ovaj zakon se primenjuje kao jedan od metoda pri utvrđivanju plagijata u „naučnim radovima” u kojima se, na primer, rezultati eksperimenta falsifikuju. Plagijatori, pre nego što odlučite da se bavite ovim neakademskim kriminalom, najpre dobro proučite Benfordov zakon!
(Naslovna ilustracija Dijagramska analiza (S. Kuestenmacher/twitter.com)