Sve je rezultat njegoševskog „soglasija opšteg”, koje se svodi na to da su u prirodi mogući samo oni sistemi koji su determinisani najboljom mogućom – simetrijom, proporcijom i harmonijom, u čijoj osnovi je zlatni presek. Kako je pre četrdeset gdina đavo došao po svoje?

Prof. dr Miloje M. Rakočević
Ni u čemu što nam se dešava
nismo sami, ni prvi ni jedini.
Ivo Andrić (Znakovi pored puta)
Pre četrdeset godina došao je đavo po svoje! Probudio sam se jednog jutra do dna svog bića pogođen neobičnom zagonetkom prirode. I kako tada, tako i danas, đavo mi ne da mira – ne prestajem da se pitam zašto je to sa životom baš tako, svodivo na samo dva pitanja (oba pitanja sa po jednim potpitanjem): 1. Svi geni svega živog, od bakterije do čoveka, sazdani su od samo četiri mala molekula, četiri specifične azotne, to jest nukleotidne baze, dve pirimidinske (jednoprstene) i dve purinske (dvoprstene); i potpitanje: zašto baš ta četiri molekula? 2. Svi proteini svega živog sazdani su od tačno dvadeset aminokiselina – dvadeset aminokiselinskih molekula; i potpitanje: zašto baš tih 20 molekula?
[Svaka od dve pirimidinske baze (timin/uracil, citozin) i dve purinske (adenin, guanin) sjedinjava se sa po jednim molekulom šećera riboze, ili dezoksiriboze, i sa po jednim molekulom fosforne kiseline, pa tako nastaje novi, još uvek relativno mali molekul – nukleotid, osnovna gradivna jedinica makromolekula ribonukleinske kiseline (RNK, sa uracilom), odnosno dezoksiribonukleinske kiseline (DNK, sa timinom)].[1]
Da bi se moglo odgovoriti na dva osnovna pitanja – zašto 4 i zašto 20 – možda se i ne mora znati hemija, ali da bi se moglo odgovoriti na dva potpitanja – zašto baš ta i takva 4 nukleotidna molekula, i zašto baš tih i takvih 20 aminokiselina – mora se biti hemičar, što se meni, više slučajnim negoli namernim izborom studija, i dogodilo (iako u gimnaziji hemiju nisam ni voleo).
Na putu ka mogućim odgovorima na postavljena pitanja postoji jedno „ali”. Postavljena pitanja spadaju u tzv. fundamentalna pitanja, a kod njih ne funkcioniše forma zašto, već jedino kako. Ne možemo odgovoriti na pitanje zašto je to tako, već jedino na pitanje – kako stoje stvari u vezi sa postavljenim pitanjem. Ne možemo znati zašto je to tako da univerzum postoji, a nije tako – da ne postoji. Ne znamo zašto je to tako da su hemijski elementi sagrađeni od atoma, a nije tako da su sagrađeni na neki drugi (i koji?) način.
[1] Broj atoma u četiri molekula koji grade informacionu ribonukleinsku kiselinu, iRNK, korespondentno sa Tablicom genetskog koda (Tabela 1), iznosi: U = 12, C = 13, A = 15, G = 16; odnosno, u parovima: UG = 28 x 1 i CA = 28 x 1. Kad poprime formu nukleotida, tada je broj atoma sledeći: U = 34, C = 35, A = 37, G = 38; odnosno, u parovima: UG = 36 x 2 i CA = 36 x 2 (uporediti: Rakočević, 1997a / 1997b, Solutions 25-29, pp. 62-63; www.rakocevcode.rs). Postavlja se pitanje: da li je ovo kuriozitet i koincidencija, ili je u pitanju izvesna prirodno-kodna suština kad sume broja atoma po parovima korspondiraju sa kvadratom prvog savršenog broja (6) i prvim stepenom drugog savršenog broja (28)? [Savršen je onaj broj koji je jednak sumi svojih činilaca.]
Jedinstven broj
Sa ovim saznanjem, pogledajmo kako stoje stvari u vezi sa dva osnovna pitanja. Prvo pitanje tiče se broja 4. Taj broj je specifičan i unikatan u tom smislu što poseduje jedno svojstvo koje ne poseduje nijedan drugi broj u nizu prirodnih brojeva. Posmatran kao celina, taj broj se sa svojom polovinom (simetrija!) nalazi u relaciji jednakosti kroz tri operacije: 2 + 2 = 2 x 2 = 22 = 4. Osim toga, relacija jednakosti ostvaruje se i kroz operaciju inverzije, i to u granicama skupa {2, 4}, gde je 24 = 42; a, takođe i u granicama proširenog skupa, proširenog sledećim parnim brojem, brojem šest {2, 4, 6}, gde je 26 = 43 = 64; a, upravo toliko ima kodovnih „reči” (kodona) u genetskom kôdu. Sve ovo nas dovodi u vezu i sa drugim značajnim relacijama, kroz odgovarajuća matematička uopštavanja.
Tako jednostavna tablica, a u njoj
sadržana kompletna priča o jednom
čudesnom jeziku – jeziku gena;
priča o četvoroslovnoj azbuci iz
koje nastaju 64 troslovne reči.
A najznačajnija veza, neposredno vidiljiva kroz ta uopštavanja, jeste ona koja predstavlja neposrednu korespondenciju izraza za genetski, i izraza za hemijski kôd, kako je i prikazano u pregledu 1 (u relaciji sa pregledom 2): mn = nm / n2 = 2n. Naravno, ova veza se može uočiti samo pod uslovom da se periodni sistem hemijskih elemenata (PSE) predstavi na adekvatan (istinit) način, kako sam i pokazao još pre 26 godina (Rakočević, 1991).[2]
[2] U pitanju je Tabela 4.1 u navedenom radu (Rakočević, 1991), koja se nalazi i u knjizi (Rakočević, 1997b), kao Tabela 18, str. 180 (www.rakocevcode.rs). Glavno u toj Tablici PSE jeste to što je 14 lantanida raspoređeno u 14 grupa, na isti način kako je to učinio Mendeljejev (Kedrov, 1977, Tablica 18, str. 188). U tom smislu, ostaje nejasno zašto već decenijama IUPAC (International Union of Pure and Applied Chemistry), u čijoj kompetenciji je, pored svega drugog u hemiji, i nomenklatura PSE, ignoriše Mendeljejeva, (stavljanjem svih 14 lantanida, zajedno sa lantanom, u treću grupu), ignorišući time i osnovni zakon hemije (koji proističe iz zakona periodičnosti), prema kojem svaki neparni elemenat mora biti u neparnoj, a parni u parnoj grupi. [IUPAC: „Project No.: 2015-039-2-200; Start Date: 18 December 2015; Division Name: Inorganic Chemistry Division; Division No.: 200. Objective: This project will deliver a recommendation in favor of the composition of group 3 of the periodic table as consisting either of: 1. the elements Sc, Y, Lu and Lr, or 2. the elements Sc, Y, La and Ac. The task group does not intend to recommend the use of a 32-column periodic table or an 18-column. This choice which is a matter of convention, rather than a scientific one, should be left to individual authors and educators.“ (Oba podvlačenja – lutecijuma i lantana – jesu moja, da bi se istaklo da IUPAC svojim projektom želi da razreši navodnu dilemu koji od ova dva elementa treba da bude upisan u treću grupu?!)]
Drugo pitanje tiče se broja 20, a da bi se sagledala njegova specifičnost i unikatnost nužno je da se tablica množenja u dekadnom brojevnom sistemu predstavi na adekvatan (istinit) način, kada je neposredno očigledno da se broj 20 u formi 20-20 nalazi tačno na sredini tablice (videti uokvireni tekst).
Što se tiče mogućeg odgovora na dva potpitanja – zašto baš ta 4 nukleotidna molekula, i baš tih 20 aminokiaelinskih molekula – potrebno je napisati bar još jednu, dobro argumentovanu, makar i malu studiju, što ovim člankom delimično i činimo.
*
Te, sada davne, 1977. godine, Tablica genetskog kôda (tabela 1) postojala je tek desetak godina, mada je predistorija njenog nastanka već uveliko nastanjivala sve srednjoškolske udžbenike širom sveta. Tako jednostavna tablica, a u njoj sadržana kompletna priča o jednom čudesnom jeziku – jeziku gena; priča o četvoroslovnoj azbuci iz koje nastaju 64 troslovne reči, za koje bi matematičari rekli da su to varijacije treće klase (sa ponavljanjem) iz skupa od četiri elementa.
I već u ovome se vidi jedinstvenost, tj. unikatnost genetskog koda. Jedino u ovom (mogućem kodogenom) slučaju važe dva osnovna mendeljejevska principa – princip minimuma promene, i princip kontinuiteta: azbuka je četvoroslovna, reč troslovna, koren reči dvoslovan, start jednoslovan. A, ako bi azbuka bila, na primer, petoslovna, poštovanjem dva navedena principa reči bi morale biti četvoroslovne, ali tada postoji neizvesnost za koren reči – da li je sa tri, ili sa dva slova?
Brojeve po dijagonali tablice množenja (Tabela 2): 0, 2, 6, 12, 20, 30, … , prepoznajemo i kao vrednosti za q u jednačini generalisanog zlatnog preseka x2 + px = q (q = 0, 2, 6, 12, 20, 30, …) u skupu familije „metalnih preseka” (Spinadel, 1998, 1999; Rakočević, 2004b), gde se rešenja tih jednačina generišu iz skupa prirodnih brojeva: (0, 1), (1, 2), (2, 3), (3, 4), (4, 5), … ; a, sve saglasno sa dva odnovna mendeljejevska principa – principa minimuma promene, i principa kontinuiteta [Prva familija „metalnih preseka”: „zlatni” (p=1; q=1), „srebrni” (p=2; q=1), „bronzani” (p=3; q=1), …; Druga familija „metalnih preseka”: „zlatni” (p=1; q=1), „bakarni” (p=1; q=2), „nikleni” (p=1; q=3, …).]
Dvostruke vrednosti brojeva koje nalazimo na dijagonali tablice množenja: 0, 4, 12, 24, 40, 60… prepoznajemo i kao vrednosti jedne od kateta Diofantovih trouglova. Uvećane za po 1 te vrednosti postaju hipotenuze istih tih Diofantovih trouglova: 1, 5, 13, 25, 41, 61itd. Kad znamo da se druga kateta Diofantovih trouglova generiše iz skupa neparnih prirodih brojeva (1, 3, 5, 7, 9, 11…), tada imamo i kompletan zapis za sve Diofantove trouglove: 0. (1, 0, 1), 1. (5, 4, 3), 2. (13, 12, 5), 3. (25, 24, 7), 4. (41, 40, 9), 5. (61, 60, 11) itd. Nadalje, kad znamo sve ove veze sa zlatnim presekom, i još znamo da je genetski kôd takođe determinisan zlatnim presekom (Rakočević, 1998), razumemo i nalaz V. Ščerbaka (V. Shcherbak), prema kome kôdiranje tzv. četvorokodonskih aminokiselina „ide” preko Pitagorine trojke (5,4,3) (Shcherbak, 1994).
Jedna ili više troslovnih reči (kodona) daju značenje slovima druge azbuke genetskog kôda, nekom od 20 aminokiselinskih molekula. A to davanje značenja nije ništa drugo do stvaranje stereohemijskih uslova za hemijsku reakciju u kojoj se nad svaka tri molekula nukleotidnih baza (koje izgrađuju dugačke niti nukleinskih kiselina DNK i RNK, kao na slikama 1 i 2), ugrađuje po jedna nova aminokiselina u proteinski lanac.
Molekul dezoksiribonukleinske kiseline (DNK) je, zapravo, makromolekul. Prilikom deobe ćelije, njegove dve spiralno uvijene niti se raspliću, ali tako da svaka od njih izgrađuje novu, sebi komplementarnu nit. Od jednog molekula nastaju dva, pa kad se ćelija podeli – dve novonastale ćelije imaju isti genetski zapis. Ali, ne samo to. Nad jednom od dve niti molekula DNK (kodogena nit) sintetizuje se jednostruka nit informacione ribonukleinske kiseline (iRNK). Ona se kreće kroz citoplazmu i tom prilikom se niz nju kotrljaju ćelijska telašca ribozomi koji su, zapravo, male fabrike za proizvodnju proteina.
Mehanizam je sledeći: transportna ribonukleinska kiselina (tRNK) koja doprema aminokiselinu, sa tri svoja slova (tri nukleotida) na suprotnom kraju od privezane aminokiseline, tzv. antikodonom, povezuje se sa tri komplementarna nukleotida iRNK. Time su stvoreni stereohemijski uslovi da se pridošla aminokiselina prisajedini prethodno povezanim aminokiselinama u proteinski lanac, kako je pokazano na slici 2. [Kao što je opštepoznato, način funkcionisanja molekula nasleđa – molekula DNK – kroz sparivanje komplementarnih nukleotida otkrili su Džejms Votson (James Watson) i Frensis Krik (Francis Crick) 1953. godine, za koje otkriće su 1962. godine dobili Nobelovu nagradu].
Iznenađenje u iznenađenju
Kada sam se prvi put, početkom sedamdesetih godina prošlog veka, istraživački udubio u tablicu genetskog kôda, bio sam u isto vreme dvaput iznenađen i začuđen. Bilo je to svojevrsno – iznenađenje u iznenađenju. Začudila me najpre jednostavnost te tablice, i činjenica da je jedan matematički izraz u potpunosti realizovan u stvarnosti; ali me još više začudilo to što se ljudi nad ovom jednostavnošću nisu dovoljno začudili. Srećom, i to se dogodilo desetak godina kasnije.
Američka hemičarka Rozmeri Svenson (Rosemarie Swanson), sa Univerziteta u Teksasu, pokazala je, 1984. godine, da se genetski kôd može svesti na grej kôd (Gray code), na odavno poznati binarni mašinski kôd u kojem se naizmenično smenjuju svetla i tamna polja. Pokazala je, naime, da se 64 genetsko-kodne reči (kodoni) mogu poređati tako da čine jedan krug u kojem se svaka sledeća reč od prethodne razlikuje tačno za jedno slovo. S pravom je slavodobitno zaključila da za genetski kôd važe dva ključna principa: princip minimuma promene i princip kontinuiteta. Prava je šteta da se tom prilikom nije setila kako su to zapravo dva izvorna mendeljejevska principa, što bi joj ukazalo na očekivanu mogućnost da to znači da genetski kod „vuče” svoje korene upravo iz periodnog sistema hemijskih elemenata (PSE).
Naoružan ovim saznanjima krenuo sam da tražim zadovoljenje mojoj radoznalosti i začuđenosti. Odlučio sam da grej kôd model i samu tablicu genetskog kôda razvijem u binarno-kôdno drvo, 0–63 (slika 3) i preispitam sve bitne odnose između osam potklasa kodona (osam okteta) u okviru celine kao svojevrsne klase sastavljene od 64 kodonske reči. Rezultati do kojih sam došao objavljeni su jednim delom, najpre u mojoj knjizi „Geni, molekul i jezik” (Naučna knjiga, 1988), a potom, u definitivnoj formi, u prestižnom internacionalnom časopisu (Biosystems, 1998).
Međutim, objavljivanje knjige je imalo svoju predistoriju. Već pripremljena za štampu ostala je da čeka nekoliko meseci tokom 1987. godine, dok se nisu završila dva moja nenadano dobijena, veoma povoljna studijska boravka u Nemačkoj, dva meseca u Berlinu i mesec dana u Minhenu, u Maks Plank institutu, u odeljenju za proteinsku hemiju. Ali, ono što je bilo neobično u mom studijskom programu, i što je pomalo iznenadilo stipenditore, bilo je to što sam tražio da se usavršavam istovremeno u istraživanju genetičkih informacija i u pretraživanju naučnih informacija. Na taj način sam se našao na izvorima svih relevantnih svetskih naučnih baza podataka, i kad sam se vratio kući moja knjiga je dopunjena posebnim dodatkom od čitavih pedesetak stranica, i sve su bile posvećene genetskom kôdu.
Videvši binarno-kôdno drvo genetskog
kôda u mojoj knjizi, nekoliko dobronamernih,
ali i nedobronamernih istraživača u
našoj sredini, upozorilo me na to da ono
podseća na isto takvo binarno drvo koje
se nalazi u kineskoj „Knjizi promena”.
Tokom boravka u Minhenu, u Maks Plank institutu, baš tada je tu nastajala Međunarodna baza proteinskih i nukleinsko-kiselinskih baza – zapisa svih do tada hemijski analiziranih makromolekula ove vrste, tako da sam na licu mesta mogao da se uverim da moj, hemijski i kodogeno zasnovan, hijejarhijski redosled 20 proteinskih aminokiselina bolje „pasuje” od službenog, sadržanog u rečenim bazama podataka.
Videvši binarno-kôdno drvo genetskog kôda u mojoj knjizi, nekoliko dobronamernih, ali i nedobronamernih istraživača u našoj sredini, upozorilo me na to da ono podseća na isto takvo binarno drvo koje se nalazi u jednoj od najstarijih knjiga na svetu, u kineskoj „Knjizi promena” (Ji-Đing), staroj oko tri hiljade godina. Bio sam skeptik i, uprkos svim upozorenjima, u početku mi nije bilo ni na kraj pameti da proverim, da pogledam o kakvoj je to starostavnoj knjizi reč. Naročito zbog toga što sam na predavanjimna iz filozofije već odavno bio saznao za izričito negativan Hegelov stav prema toj knjizi.
Izvorni ključ života
Do preokreta je došlo kad mi je, jednom potpuno slučajnom okolnošću (najpre na nemačkom, a potom i na engleskom) dopala ruku knjiga, za mene tada neočekivanog naslova, „Ji Đing i genetski kôd”, s podnaslovom „Zaboravljeni ključ života”. Autor je bio nemački lekar Martin Šenberger (Martin Schoenberger), koji je odmah nakon obelodanjivanja genetskog kôda uvideo moguću analogiju i vezu. [Martin Šenberger je knjigu objavio 1973. godine. Kasnije sam našao da je poznati molekularni biolog Ganter Stent (Gunther S. Stent) još 1969. objavio knjigu The comming of the golden age u kojoj je analizirao analogije i veze između genetskog kôda i „Ji Đinga”, tako da mu pripada prioritet].
Kinezi nisu čekali na nas iz trećeg
milenijuma, nego su pre tri hiljade
godina na osnovu 64 heksagrama na
šestobitnom binarno-kôdnom drvetu
izgradili svoje pismo i filozofiju.
Ponovo je đavo došao po svoje! Moje istraživačke obaveze su se udvostručile. Sada je trebalo istraživati ne samo genetski kôd već i stvaralaštvo starih naroda i klasika, a sve s ciljem da se odgonetne moguće „soglasije opšte”, kako bi rekao Njegoš, i da se vidi u čemu je tajna: da li je genetski kôd, možda, samo jedan aspekt nekog univerzalnog kôda prirode i koje bi bile karakteristike jednog takvog kôda?
Silom prilika moja istraživanja su morala da krenu dvema linijama. Jedna je bila tajna, a druga javna. Ono što je bilo na tajnoj liniji ni za živu glavu nisam smeo da objavim u bilo kojem od zvaničnih naučnih časopisa, jer bih odmah bio optužen za numerologiju. „Ali, ako ne u časopisima, objaviću u knjigama, što na srpskom, što na engleskom jeziku”, tako sam rezonovao. I sada svako može da nađe moju knjigu Genetic code as a unique system (Studentski kulturni centar u Nišu, Bina u Beogradu, 2007b, str. 60), ako ne u knjižarama, a ono na mom sajtu (www.rakocevcode.rs), i uveri se da zlatni presek, savršeni i prijateljski brojevi zaista jesu determinante genetskog kôda – determinante sekvence prirodnih brojeva 0-63 (tabela 3).
[Ako je čitaocu prejak izraz determinante, može se reći da aminokiseline korespondiraju s rečenim entitetima–kvantitetima, preko logičke relacije: „ako–onda”: ako zlatni presek linearne duži 0–63 pada između brojeva 38 i 39, a na tim pozicijama se nalaze kodoni CAA i CAG koji kodiraju aminokiselinu glutamin, onda je ona „zlatna” aminokiselina, na poziciji f^1(fi na prvi stepen); istim postupkom se nadalje otkrivaju i preostale „zlatne” aminokiseline, na pozicijama od f^2 do f^9 (slika 3 u relaciji s tabelom 3]
Šestobitno binarno drvo je posebno i specifično, pored svega drugog i po tome što je jedino na njemu zbir brojeva na dvema unutrašnjim granama (dva okteta) toliki da odgovara prvom paru prijateljskih brojeva (220 + 284 = 504), a po dve susedne grane se dopunjuju do njihovog zbira (504); sve zajedno, realizuje se svojevrsni logički kvadrat: (0) 220 + 284 = 504; (1) 156 + 348 = 504; (2) 92 + 412 = 504; (3) 28 + 476 = 504. S druge strane, zbir brojeva prvog kvarteta iznosi 6, prvog okteta 28; zbir brojeva na levoj grani (što se podudara sa zbirom brojeva u prvoj polovini tablice GK), od 0 do 31, iznosi 496, što je redom realizacija prva tri savršena broja (6, 28, 496).
Ako, pak, izbrojimo sve brojeve 0-63, pa se vratimo natrag (cikličnost!), pri čemu broj 0 postaje 127, pa sve brojeve sekvence 0-127 saberemo, dobićemo kao rezultat 8128, što je zapravo četvrti savršeni broj. Nakon ovih uvida postaje jasno zašto Kinezi nisu čekali na nas iz trećeg milenijuma, nego su sve ovo još pre tri hiljada godina uvideli i na osnovu 64 heksagrama na šestobitnom binarno-kôdnom drvetu izgradili ne samo svoje pismo i filozofiju nego podatkali i osnove svoje kulture.
Da bi se potvrdilo da sve ovo ima ne samo kodogeni već i hemijski smisao, trebalo je „zlatnim” aminokiselinama pridružiti njihove hemijske komplemente i ispitati moguće ravnoteže, saglasnosti i pravilnosti (Rakočević, 1998, Survey 2.1 & 2.2, p. 289). [„Zlatne” aminokiseline: (F, L, Q, T, P, S, G); „zlatne” aminokiseline s pridruženim hemijakim komplementima: (F-Y, L-A, Q-N, T-M, P-I, S-C, G-V); preostali hemijski nekomplementi, šest AK, spakovanih u tri hemijska para: (D-E, K-R, H-W.] Ovo hemijsko sparivanje 20 AK u deset parova bilo je, u nauci o genetskom kôdu, prvo predočavanje da iz hemijske prirode 20 proteinskih aminokiselina neminovno slede deset aminokiselinskih parova (Rakočević, 1998, Biosystems, 46, 283-291).[3]
Broj atoma u bočnim nizovima molekula predočenih triju klasa aminokiselina razlikuje se tačno za (1 x 6), (2 x 6) i (3 x 6). Naime, u sedam „zlatnih aminokiselina” ima tačno 60 atoma, a u njihovih sedam komplemenata – isto toliko plus (1 x 6), što ukupno iznosi 66; u preostalih šest nekomplemenata ima 66 plus (2 x 6) atoma što je ukupno 78 atoma. Ako „zlatne aminokiseline” napišemo ne redosledom kako su skinute s binarnog drveta već redosledom prema broju atoma koje u sebi poseduju, zajedno sa njihovim komplementima (G-V, S-C, T-M, P-I, Q-N, L-A, F-Y), i ispred njih se dodaju tri para nekomplemenata, tada se dobija uređen sistem proteinskih AK, prema pozicijama njihovih atoma u PSE, koji sam nazvao Cyclic Invariant Periodic System, u skraćenoj formi CIPS: {H-W, K-R, D-E (G-V [S-C, T-M] P-I), Q-N, L-A, F-Y}.
Kako vidimo, dobijaju se četiri klase aminokiselina, prema hemijskoj sličnosti, tri klase alaninskog stereohemijskog tipa, i jedna klasa nealaninskog tipa (Popov, 1989; Rakočević & Jokić, 1996). U sredini se nalaze četiri halkogene AK (imaju kiseonik, ili sumor u bočnom nizu): S-C, T-M; u sledećem ciklusu nalaze se četiri AK nealaninskog tipa: G-V, P-I; sledi ciklus jedine dve A AK koje poseduju karboksilnu grupu u bočnom nizu, zajedno sa njihova dva amidna derivata: D-E, Q-N; potom dolaze četiri alifatične aminokiseline: K-R, L-A; konačno, u poslednjem ciklusu nalaze se četiri aromatične aminokiseline, hemijski kompleksnije od alifatičnih: H-W, F-Y (uporediti: Rakočević, 2011, Fig. 6, p. 832).
[3] Nomenklatura proteinskih aminokiselina: alanin (Alanine, A), arginin (ARginine, R), asparagin (AsparagiNe, N), asparaginska kiselina (Aspartic acid, D), cistein (Cysteine, C), glutamin (Glutamine, Q), glutaminska kiselina (Glutamic acid, E), glicin (Glycine, G), histidin (Histidine, H), izoleucin (Isoleucine, I), leucin (Leucine, L), lizin (Lysine, K), metionin (Methionine, M), fenilalanin (Phenylalanine, F), prolin (Proline, P), serin (Serine, S), treonin (Threonine, T), triptofan (Tryptophan, W), tirozin (Tyrosine, Y), valin (Valine, V).
Put kojim se teže ide
Neznano kako i zašto, tek dogodilo se to da gore citirani rad E. M. Popova (Evgeniй Mitrofanovič Popov), iz 1989. godine, osim mene skoro niko više ne citira, kad je reč o primenama na genetski kôd.[4] A, bez činjenica saopštenih u njegovom radu genetski kôd praktično nije moguće razumeti; sledstveno tome, nije moguće razumeti postanak i suštinu života u univerzumu, pa se time ne može imati ni adekvatna biologija, niti medicina.
Pa, koje su to, onda, činjenice? Evo ih, belodano date na slici 4. Na samom početku data je formula najjednostavnije proteinske aminokiseline, glicina: za „glavu” te aminokiseline (za aminokiselinsku funkcionalnu grupu), jednu te istu u svih 20 aminokiselina, prikačeno je „telo” (bočni niz) od samo jednog atoma vodonika. Drugim rečima, između glave i tela nema ničeg umetnutog.
Tek sa uvidom u postojanje četiri tipa
diverziteta proteinskih aminokiselina,
bili su stvoreni uslovi da se uoči veza
između genetskog i hemijskog kôda, i to
kroz analogije, koje su i više od toga.
Međutim, ako posmatramo sledeću aminokiselinu (sledeću po hemijskoj složenosti), alanin, vidimo da je između glave i tela umetnuta jedna CH2 grupa. Ali, kad se upoznamo s radom E. M. Popova o četiri stereohemijska tipa proteinskih aminokiselina, tada uočavamo da čak još 15 aminokiselina imaju istu tu CH2 grupu između glave i tela. [Izuzetak je samo treonin u kome je jedan atom vodinika CH2 grupe supstituisan CH3 grupom (slika 4 druga kolona, treći red).] To, onda, znači da 16 aminokiselina pripada alaninskom stereohemijskom tipu, a samo jedna (glicin) pripada glicinskom stereohemijskom tipu.
Izborom glicina, priroda je iz neugljovodoničnosti izabrala najednostavniji mogući slučaj; ne uzima nadalje nijedan drugi, već prelazi na ugljovodoničnost, i iz otvorenog ugljovodoničnog niza uzima, takođe prvi mogući slučaj, metil grupu (CH3) iz najednostavnijeg organskog molekula, metana, i vezuje je za glavu aminokiseline – nastaje alanin. Očekivalo bi se da sledeća za vezivanje bude etil grupa (CH3-CH2), ali to se ne događa. Priroda i ovde – iz otvorenosti – uzima prvi mogući slučaj, i prelazi na polucikličnost[5] (slika 4, treća kolona, prvi red).]: „trougao” izopropil grupe veže se svojim „temenom” za glavu aminokiseline, nastaje valin; potom se veže svojom stranicom, pa nastaje prvi mogući ciklični aminokiselinski molekul, prolin (slika 4, druga kolona, prvi red).
[4] Teško je verovati, ali razlog bi mogao biti u činjenici da tzv. „Zapad“ sa potcenjivanjem gleda na rusku nauku. Tako, ozbiljan istraživač će sa nevericom utvrditi da se i danas na Zapadu u istu ravan stavljaju Dmitrij Ivanovič Mendeljejev i Lotar Majer, kad je reč o periodnog sistemu hemijskih elemenata. Navodno su „istu stvar“ obojica otkrili, nezavisno jedan od drugog, iako je samo Mendeljejev otkrio Zakon periodičnosti.
[5] Naravno, ni u jednom udžbeniku organske hemije, na čitavom svetu, ne može se naći pojam „polucikličnost“ molekula, ali priroda ne može da „preskače“, već se uvek ponaša u skladu sa dva prirodna principa, koje prepoznajemo kao mendeljejevske principe – sa principom minimuma promene i principom kontinuiteta.
Nakon toga priroda prelazi na račvastost. Prvi slučaj račvanja otvorenog niza moguć je tek sa četri atoma ugljenika: nastaju dve izomerne aminokiseline, leucin i izoleucin (slika 4, druga kolona, prvi red). Sa ovim su sva četiri stereohemijska tipa proteinskih aminokiselina generisana: glicinski (sa glicinom), prolinski (sa prolinom), valinski (sa valinom i izoleucinom), alaninski, sa preostalih 16 aminokiselina. Ključno u stereohemijskoj geometriji jeste sloboda rotacije oko hemijske veze koja povezuje glavu i telo aminokiseline: u slučaju glicina stoprocentna sloboda rotacije; u slučaju prolina rotacija nije moguća; u preostala dva tipa moguća je delimična rotacija, kod alaninskog tipa bliža modelu glicina, a kod valinskog bliža modelu prolina – nijansiranje, kao i u svemu drugom, kad je u pitanju genetski kod. Podrazumeva se da ne može biti drugačije nego da se ova svojstva aminokiselina odražavaju na strukturu i funkciju proteina, upravo od aminokiseina sagrađenih.
Takođe ne može biti drugačije nego to da predočena geometrija jeste samo jedan aspekt daleko šire geometrije genetskog koda, koja se svojom ukupnošću, a posebno preko zlatnog preseka odražava i na proteine, pa time i na sâm život – od najjednostavnijih do najsloženijih organizama.[6]
*
Kad jednom saznamo o neminovnosti postojanja četiri stereohemijska tipa proteinskih aminokiselina, tada smo na dobrom (i teškom!) putu da
[6] Primera radi, nobelovac Manfred Ajgen (Manfred Eigen), zajedno sa svojim kolegom Peterom Šusterom (Peter Schuster), i sâmu Tablicu genetskog koda predočio je, devedesetih godina prošlog veka, u formi trodimenzionalne kocke. Rozmeri Svenson, u već citiranom radu (Swanson, 1984) govori o „kocki kodonskog puta“. Što se, pak, mene tiče, u svojoj knjizi iz 1994. godine predočio sam LIGHT (Logical–Information–Geometric–Homomorphic–Topological) model kocke (Rakočević, 1994) koji važi, kako za Tablicu, tako i za binarno drvo genetskog koda; model u kome se integrišu logička, informaciona, geometrijska i topološka suština standardnog genetskog koda. U najnovije vreme (12. juna 2017.), u časopisu „Frontiers in Computational Neuroscience“, objavljena je vest o naučnom rezultatu [„Scientists discover hidden patterns of brain activity, École polytechnique fédérale de Lausanne (EPFL)“], prema kome se informacije koje se generišu u moždanim neuronima eksprimiraju u formi specifičnih geometrijskih obrazaca, što je u nauci potpuna novost. Moja hipoteza (i predikcija!), tokom višedecenijskog istraživanja genetskog koda, sve vreme je bila ta da se ukupna geometrija i stereohemija genetskog koda moraju eksprimirati u strukturi i funkciji proteina, a to znači i u sâm život, ma gde on bio u Univerzumu, u čemu i jeste smisao traganja za adekvatnom biologijom i medicinom.
uvidimo i postojanje četiri tipa diverziteta istih tih – proteinskih aminokiselina. Uočavamo da postoje tačno četiri aminokiseline u čijem bočnom nizu se nalaze hemijski elementi ugljenik i vodonik i nijedan drugi. Kažemo da su to standardne ugljovodonične aminokiseline. Ali takođe lako uočavamo da postoje i dve nestandarne, takođe ugljovodonične:[7] glicin i prolin.[8]
U daljem traganju za postojanjem tipova diverziteta, uočavamo da postoji tačno osam aminokiselina kod kojih se funkcionalne grupe iz glave aminokiseline preslikavaju i u telo, u bočni niz. Preostaje šest aminokiselina kod kojih nema tog preslikavanja. Sve zajedno, dobijamo četiri (diverzitetski različite) klase aminokiselina, uređenih po hemijskim parovima: [(G, P), (A-L, V-I), (C-M, F-Y, H-W), (S-T, D-E, N-Q, K-R)].
Sa aspekta razlikovanja u osnovnom fizičko-hemijskom svojstvu, dve nestandardne ugljovodonične aminokiseline su semipolarne; četri ugljovodonične nepolarne; osam aminokiselina kod kojih postoji rečeno preslikavanje jesu polarne; i, konačno, preostalih šest aminokiselina predstavljaju kombinaciju nepolarnih, polarnih i semipolarnih. [Semipolarna je triftofan (W), polarne su histidin (H) i tirozin (Y), a nepolarne su: fenilanalin (F), cistein (C) i metionin (M).]
Tek sa uvidom u postojanje četiri tipa diverziteta proteinskih aminokiselina, bili su stvoreni uslovi da se uoči veza između genetskog i hemijskog kôda, i to kroz analogije, koje su i više od toga (one su suštinske karakteristike i jednog i drugog kôda). Pokazuje se, naime, da je kodiranje u oba kôda zasnovano na istom modelu. To je sistem od dve lenearne jednačine čija desna strana kod sumiranja x + y daje, u prvoj jednačini kvadrat broja 5, a u drugoj kvadrat broja 6; u slučaju razlika x – y rezultat je kvadrat broja 3 i broja 4.
U stvarnosti to znači sledeće: u standardnom genetskom kôdu postoji tačno 61 aminokiselinski kodon (daju značenje aminokiselinama) i 3 „stop” kodona (označavaju „stop” situacije, tj. prekid u sintezi proteina). Od 61 aminokiselinskih kodona, 25 se troši na kôdiranje 2+4 manje kompleksnih aminokiselina, onih koje u bočnom nizu sadrže samo elemente vodonik i ugljenik (kod glicina je samo vodonik).
S druge strane, 36 kodona se troši na kodiranje kompleksnijih aminokiselina, njih 6+8, kod kojih u bočnom nizu osim ugljenika i vodonika postoji bar još jedan elemenat – kiseonik, ili azot, ili sumpor. Dalji tok distribucije je, kako sledi. Rešenja linearne jednačine čija je desna strana 25, jesu 8 i 17, a to odgovara broju kodona u procesu kodiranja: 8 kodona kodira dve nestandardne ugljovodonične aminokiseline, a 17 kodona kodira četiri standardne ugljovodonične aminokiseline.
Linearna jednačina čija je desna strana 36 ima rešenja 10 i 26; od toga, 10 kodona se troši na kodiranje šest aminokiselina koje nemaju preslikavanje glava–telo, a 26 kodona na kodiranje onih osam aminokiselina koje preslikavanje glava–telo poseduju.
*
Analogne situacije postoje i u hemijskom kôdu, ovaploćenom u Periodnom sistemu hemijskih elemenata, kad se PSE posmatra do granice stabilnosti/nestabilnosti, do polonijuma (P-84). U tom skupu, 20 monoizotopnih elemenata odgovara stanju od 20 nekodonskih situacija (20 aminokiselina), 61 višeizotopni elemenat odgovara stanju „61 aminokiselinski kodon”, a tri prekida u stabilnoj izotopiji (tehnecijum, Tc; prometijum, Pm i polonijum, Po) odgovaraju trima „stop“ kodonima u standardnom genetskom kodu.
Nadalje se skup od 61 višeizotopnog elementa razbija tačno kao i u genetskom kôdu, na 25 i 36. Pri tome, 25 hemijskih elemenata su manje stabilni, a 36 su više stabilni. [Manje stabilni, nestabilni, u smislu da svaki od njih poseduje bar po jedan primordijalni nestabilni izotop; više stabilni, stabilni u smislu da nijedan od tih 36 elemenata ne poseduje nestabilne izotope, već samo stabilne.] Dalja distinkcija ide po istim onim dvema linearnim jednačinama koje važe za genestki kôd, i to u sledećem smislu: 25 nestabilnih elemenata, njih osam, nalazi se u neparnim grupama periodnog sistema, dok se njih 17 nalaze u parnim grupama periodnog sistema, takvog PSE, kakav je dat pre 26 godina (Rakočević, 1991).
Na približno isti način izvedena je distinkcija u skupu od 36 stabilnih elemenata, s malim pomeranjem u rešenjima linearne jednačine; umesto x = 10 i y = 26, ovde imamo rešenja x = 13 i y = 23. U realnosti to znači da se 13 stabilnih elemenata nalaze u neparnim grupama PSE, a 23 u parnim. (Detalje videti u članku Genetic code and periodic system: some analogies na sajtu www.rakocevcode.rs)[9]
Ovim se završava dokazni postupak u pokušaju da se odgovori i na dva potpitanja, sa početka ovog članka – zašto baš ta četiri molekula u izgradnji makromolekula DNK i RNK; i zašto baš tih 20 aminokiselinskih molekula u izgradnji makromolekula proteina? Odgovor je u predočenim jedinstvenostima i jednostavnostima tih molekula (proisteklih iz jednostavnosti atoma koji ih grade), i u korespondenciji njihovih kodirajućih aranžmana sa jedinstvenim i jednostavnim matematičkim pravilnostima i zakonitostima.
Nema te matematičke teorije verovatnoće kojom bi se moglo pokazati da sve ovo, što je gore izloženo, jeste slučajno. Naprotiv, sve je rezultat njegoševskog „soglasija opšteg”, koje se svodi na to da su u prirodi mogući samo oni sistemi koji su determinisani najboljom mogućom – simetrijom, proporcijom i harmonijom, u čijoj osnovi je zlatni presek.
[7] Uprkos tome što u bočnom nizu ima samo vodonikov atom, glicin je takođe ugljovodonična aminokiselina, s obzirom na to da u glavi poseduje ugljenik.
[8] Nestandardnost prolina potiče otuda što kod njega postoje povezanost glave i tela.
[9] Predočeno „pomeranje“ za 03 / 13, 23 drugačije je od svih drugih, mogućih u datoj linearnoj jednačini, sa aspekta važenja/nevaženja principa sličnosti i samosličnosti: (01 / 11, 25), (02 / 12, 24), (03 / 13, 23), (04 / 14, 22), itd.
ILUSTRACIJE

Pregled 1. Eksponencijalni izrazi prema kojima su generisani prirodni kodovi: levo – hemijski kod; i desno – genetski kod. Prema izrazima na levoj strani generiše se Tablica periodnog sistema hemijskih eeenata (PSE); odnose se na raspored elemenata do granice stabilnosti, do polonijuma, koji je 84. elemenat, sa 84 protona u jezgru attoma. Po 9 elemenata nalaze se u jednoj grupi osam puta; po 4 elementa dva puta, i po jedan elemenat četiri puta. Prema izrazima na desnoj strani generiše se Tablica genetskog kôda (tabela 1), sa 4 singleta, 16 dubleta i 64 tripleta; takođe i binarno drvo (slika 3) sa 2, 4, 5, 16 i 32 grane respektivno; u čestom koraku generišu se 64 kodonska tripleta.
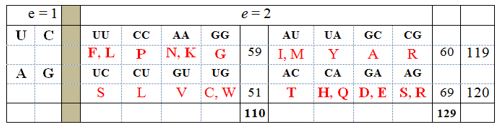
Pregled 2. Generisanje 16 nukleotidnih dubleta iz četvoroslovne genetsko-kodne azbuke, prema izrazu mn (m = 4; n = 2; e = eksponent). Ako je e = 1, tada imao četiri singleta, četiri baze – dve pirimidinske (uracil, U i citozin, C), sa po jedim prstenom u molekulu (hemijski jednostavnije), i dve purinske (adenin, A i glutamin, G), sa po dva prstena u molekulu (hemijski kompleksnije). Ako je e = 2, tada imao 16 nukleotidnih dubleta. Ako se dubleti urede po hemijskoj hijerarhiji (najpre jednostavniji UU, CC; potom kompleksniji AA, GG), tada vidimo da je ovu hemijsku suštinu prati ravnoteža broja atoma u bočnim nizovima aminokiselina, koje su tim dubletima kodirene (sve saglasno Aristotelovoj ideji o jedinstvu forme i suštine).
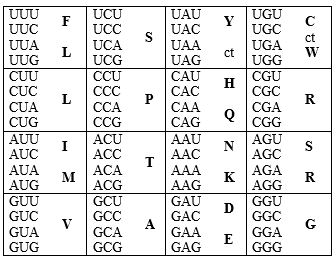
Tabela 1. Tablica standardnog genetskog kôda. Od tri moguća aranžmana (isto slovo po 16 puta, respektivno – u prvoj, drugoj, ili trećoj poziciji) ovde je dat onaj koji najbolje odgovara hemijskoj sličnosti, kako kodona, tako i aminokiselina (Crick, 1968).
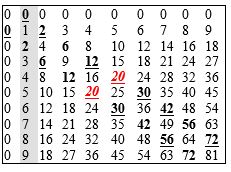
Tabela 2. Tablica množenja u dekadnom brojevnom sistemu (sa brojem 20 u sredini, u formi dubleta 20-20).

Tabela 3. Sekvenca niza prirodnih brojeva 0-63. Ako se uredi po oktetima, što je slučaj u GK (slika 3), tada je ta sekvenca strogo determinisana prvim parom tzv. prijateljskih brojeva (220 i 284), kao i trećim savršenim brojem (496). Osim toga, suma svaka dva okteta dopunjuje se do sume prva dva prijateljska broja, korespondentno sa logičkim kvadratom: (0) 220 + 284 = 504; (1) 156 + 348 = 504; (2) 92 + 412 = 504; (3) 28 + 476 = 504. Ovo ovako moguće je samo na šesto-bitnom binarnom drvetu, čime se potvrđuje njegova unikatnost, a time i unikatnost genetskog koda. [U prijateljskom paru suma činilaca prvog broja daje drugi, i obrnuto; a, savršen je onaj broj koji je jednak sumi svojih činilaca.]
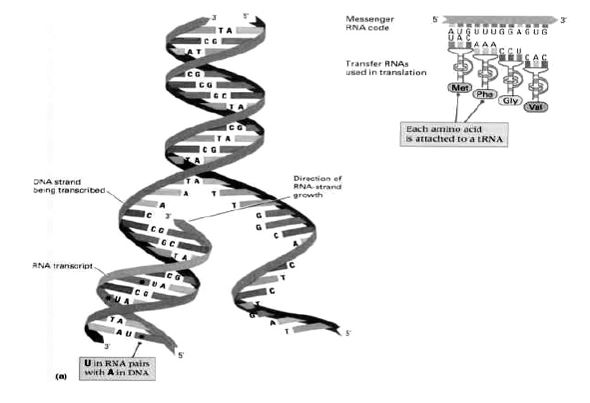
Slika1. Molekul dezoksiribonukleinske kiseline – makromolekul nasleđa (DNK). Rasplitanjem dve niti pri deobi generativne ćelije, jedna nit ostaje majci, a druga, u istovetnom zapisu se predaje ćerki-ćeliji; pritom svaka od dve nove niti dogradi sebi nedostajuću, komplementarnu nit.
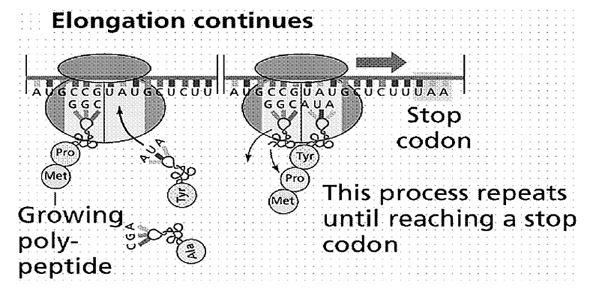
Slika 2. Rezultat genetskog kodiranja: nad jednom od dve niti makromolekula DNK sintetizuje se jednostruka nit ribonukleinske kiseline (RNK), niz koju se u citoplazmi ćelije kotrljaju mala loptasta telašca – ribozomi. Na njima se generiše sistem kodon-antikodon (kodoni na informacionoj i antikodoni na transportnoj RNK), sa donošenjem odgovarajuće aminokiseline (pomoću transportne RNK). Potom, kao na šivaćoj mašini, prišivaju se jedna po jedna aminokiselina, dobija se polipeptidni lanac, kao osnovna nit za izgradnju makromolekula proteina.
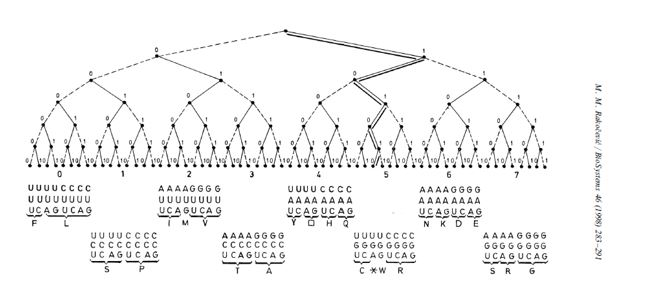
Slika 3. Šestobitno binarno drvo genetskog koda, sa rasporedom 64 troslovne „reči” (kodona), generisanih iz četvoroslovne azbuke (U,C,A,G), od početne, to jest nulte, UUU (000000), preko harmonijske (u poziciji harmonijske sredine), sa najvećom promenom, UGA 101010, do poslednje, na poziciji 63 (111111). [Prema: M. M. Rakočević, BioSystems 46 (1998), 283–291.]
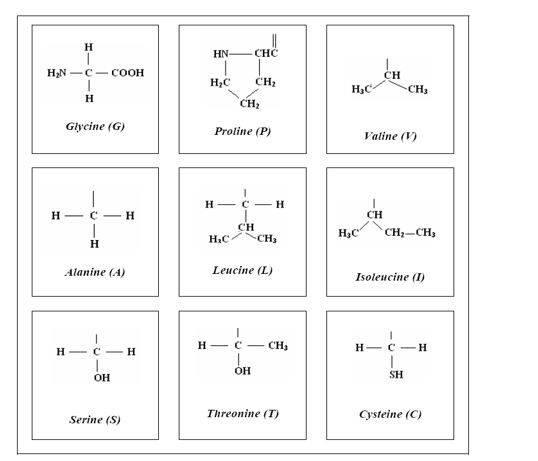
Slika 4. Strukturna formula glicina i bočnog niza preostalih 19 proteinskih aminokiselina. Formule korespondiraju sa četiri stereohemijska tipa: glicinski (sa glicinom), prolinski (sa prolinom), valinski (sa valinom i izoleucinom), alaninski, sa preostalih 16 aminokiselina, od kojih je ovde prikazano pet karakterističnih.
REFERENCE
Crick, F.H.C. (1968) The origin of the genetic code, J. Mol. Biol., 38, 367- 379, 1968.
Kedrov, B.M. (1977) Prognozы D.I. Mendeleeva v atomistike, Atomizdat, Moskva.
Popov, E. M. (1989) Strukturnaя organizaciя belkov, Nauka, Moskva.
Rakočević, M.M (1991) The coherence of the chemical and genetic code, Zbornik radova Filozofskog fakulteta u Nišu, Sekcija za hemiju, 2, 1-29 (Tabela 4.1; ova Tabela se nalazi i u knjizi: Rakočević, 1997b, kao Tabela 18).
Rakočević, M. M. (1988) Geni, molekuli, jezik, Naučna knjiga, Beograd. (www.rakocevcode.rs)
Rakočević, M. M. (1994) Logic of the Genetic Code, Naučna knjiga, Beograd. (www.rakocevcode.rs)
Rakočević, M. M.1(997a). Two classes of the amino acyl-tRNA synthetases in correspondence with the Codon path cube. Bull. Math. Biol. 59, 645-648.
Rakočević, M. M. (1997b) Genetic code as a unique system, Studentski kulturni centar u Nišu, Bina u Beogradu. (www.rakocevcode.rs)
Rakočević, M. M. (1998) The genetic code as a Golden mean determined system, Biosystems, 46, 283-291, (www.rakocevcode.rs).
Rakočević, M. M. (2004a) A harmonic structure of the genetic code, Journal of Theoretical Biology, 229, 221-234 (www.rakocevcode.rs)
Rakočević, M. M. (2004b) Further generalization of Golden mean in relation to Euler’s „divine“ equation, FME Transactions (Faculty of Mechanical Engineering, Belgrade, Serbia), 32, 95-98, 2004; arXiv:math/0611095v1[math.GM]. (www.rakocevcode.rs)
Rakočević M. M. (2011) Genetic code as a coherent system, NeuroQuantology, 9 (4), 821-841.
Rakočević, M., Jokić (1996) Four Stereochemical Types of Protein Amino Acids: Synchronic Determination with Chemical Characteristics, Atom and Nucleon Number, J Theor. Biol., 183, 345–349.
Shcherbak, V. I. (1994) Sixty-four Triplets and 20 Canonical Amino Acids of the Genetic Code: the Arithmetical Regularities. Part II. J. Theor. Biol. 166, 475-477.
Spinadel, V. W. de. (1998) From the Golden Mean to Chaos, Buenos Aires.
Spinadel, V.W. de. (1999) The family of metallic means, Visual Mathematics,1, No. 3. (http//members.tripod.com/vismath1/spinadel/).
Swanson, R. (1984) A unifying concept for the amino acid code, Bull. Math. Biol., 46, 187-207.





Zasto postoje 3 stop kodona?
Do odgovora na ovo pitanje doći ćete na sledeći način. Otvorite moj sajt http://www.rakocevcode.rs i u rubrici „pretraga“ otkucajte NQ [Rakočević M. M. (2011) Genetic code as a coherent system, NeuroQuantology, 9 (4), 821-841]. Uzmite u postupak „Table 4“, u relaciji sa „Figure 3“ i „Table 6“. Radi se o tome da aminokislinskih kodona mora biti 25 + 36 (plus 3 stop kodona); 25 kodona kodirajućih za aminokiseline niže kompleksnosti (u bočnom nizu poseduju samo vodonik ili vodonik i ugljenik) i 36 kodona, kodirajućih za aminokiseline više kompleksnosti. Želim Vam pun uspeh.
Miloje M. Rakočević
Dragi gospodine Rakocevic,
dalu ste culi za izjavu Nikole Tesle kojom je opisao mnoge naucnike?
„Mnogi naucnici od samog pocetka ne razmisle dobro i neznaju da od samog pocetka grese!“
Dali ste Vi sigurni u to sta Vi izjavljujete i o cemu pisete i o cemu predajete ?
Sta ako ste pogresili?
To sto ste Vi izjavili je simetralna perfekcija spajanja perfektno simetralnih srodnih hemijskih i fizikalnih i matematickih i bioloskih jedinjenja- spajanje srodnih stanica- inses, po tom principu je napravljena atomska bomba, nasilno spajanje srodnih atoma.
Ja Vam moram nesto reci,
u PRIRODI ne pistoji identican Atom s drugim, Atom je ziv i ima energiju i krece se, u zavisnosti od brzine i velicine kojom se spaja se na polovima s drugim polom drugog atoma koji nije istog magnetskog naboja, princip
Mesec Zemlja Sunce.
Zlatni presek se ne desava tacno u sredini , jer da je po toj vasoj perfekciji nastao zivot, zivot se nebi ni desio.
Za vrsta perfekcije postoji samo u onima koji su dosli na tu ideju da na taj nacin prave atomsko i biolosko oruzje koje ubija i truje, igrate se sa opasnim stvarima i mislite da ste pametni.
Genetska manipulacija je nasilno spajanje srodnih stanica.
Ljudski telo zivotinjsko telo biljno telo je nasilno „smuckano“ jedno s drugim.
Vatikanski naucnici glume pamet i misle da su pametniji od Tvorca i Majke Prirode, a Vi ste ucili po njihovim knjigama i ugledali se na budu, sve laz, to se moze tako ali to nije DOBRO.
Vi kao naucnik imate veliku odgovornost sta cete da izjavljujete i da tvrdite, a ne da slusate na sta Vas nagovara djavo, zasto ovo zasto ono, niste ni svesni koliko ste u pravu sto se tice djavola, on Vam pokaze perfekciju i Vi se zadivite kako je sve jedinstveno perfektno, perfekcija je zlo covece.
Par i par se ne spaja
nepar i nepar se ne spaja
ako hoces da dobijes zdravu materiju
Slepo crevo nije greske prirode
nego genetsko manipulisan crv vatikanskih naucnika kojeg su pustili u prirodu i on se ugnezdio u svim organizmima, zakacio se za creva, parazit koji se hrani od naseg organizma i producira crve kao sto je i on i ubrizgava u probavni sistem iz kojeg dospjevaju i u krv i u kostanu srz jer su osmisljeni i napravljeni i bore se za zivot.
Meso se ne jede, riba se ne jede, kukci se ne jedu, crvi se ne jedu,
Da bi procistio organizam pij caj i jedi samo povrce, sto manje to bolje, treniraj, treniraj misli,
ja sam zdrav ja sam uman
dobro ne ovosi o zlu
zlo se desava samo na Planeti Majci
u coveku jer su se neki uspeotivili Tvorcu.
Ja Vama ne zelim da pametujem jer ovo sto sam ja napisala nista nije moje novootkrice, to su znali mnogi ljudi pre mene, ja sam dosta vremena provodila uz Nikolu Teslu i Svetozara Radisica, bilo bi dobro da se obratite njima a ne Kinezima.
Sretno.