Problem se odnosi na broj jednakih sfera koje dodiruju datu sferu iste veličine. Nastao je nakon diskusije čuvenih matematičara Isaka Njutna i Dejvida Gregorija 1694. godine. Čuven je iz više razloga: 1) formulacija je ne samo elegantna, geometrijski atraktivna, već i vrlo jednostavna; 2) uprkos jednostavne postavke, bilo je potrebno 250 godina da se dođe do rešenja.

Prof. dr Miodrag Petković
Pakovanje sfera, poznato kao Gregori-Njutnov problem ili problem dodirujućih sfera, odnosi se na broj jednakih sfera koje dodiruju datu sferu iste veličine. O ovome su dosta su diskutovali Dejvid Gregori (David Gregory, 1659-1708) i Isak Njutn (Isaac Newton, 1643-1727) tokom 1694. godine. Prvi je bio najpre profesor matematike u Edinburgu, a kasnije profesor astronomije na Univerzitetu u Oksfordu, a drugi profesor matematike na Univerzitetu u Kembridžu. Prema istoričarima matematike i raspoloživim dokumentima, diskusije su se vodile prilikom njihovih susreta u Kembridžu ili Oksfordu. Pomenuti problem i njima slični privukli su pažnju velikog broja čuvenih matematičara, kao što su Dirihle, Gaus, Ermit, Lagranž, Minkovski, a i mnogi u današnje vreme.
Problem je čuven iz više razloga: 1) formulacija je ne samo elegantna, geometrijski atraktivna, već i vrlo jednostavna; 2) uprkos jednostavne postavke, bilo je potrebno 250 godina da se dođe do rešenja. Slavni matematičar David Hilbert jednom prilikom je rekao da je prvi kriterijum za dobar matematički problem taj da se on može s lakoćom objasniti „prvoj osobi koju sretnete na ulici”. Možda ovo nije kvalifikacija univerzalnog tipa, ali se ispostavilo da neki od najčuvenijih matematičkih problema zaista zadovoljavaju Hilbertov kriterijum, kao što su Fermaova poslednja teorema (dokazana posle 360 godina), problem četiri boje (rešen posle 116 godina), Keplerov problem optimalnog pakovanja sfera (rešen posle skoro 400 godina), Goldbahov problem o prostim brojevima (još nije rešen). Ovim problemima, svakako, treba pridodati Gregori-Njutnov problem dodirujućih sfera.

Sl. 1 Oksfordska diskusija D. Gregorija i
I. Njutna (Foto i dizajn V. Petković)
Dejvid Gregori bio je nećak čuvenijeg matematičara Džejmsa Gregorija (James Gregory, 1638-1675). Postao je profesor matematike u svojoj 24. godini na Univerzitetu u Edinburgu gde je predavao Njutnove teorije. Dejvid Gregori je jako podržavao Njutna u istorijskoj raspravi s Lajbnicom u vezi s prioritetom u otkriću integralnog i diferencijalnog računa. S druge strane, Njutn je mnogo pomogao Dejvidu Gregoriju da ostvari uspešnu karijeru.
Problem dodirujućih sfera proizašao je kao rezultat čuvene diskusije između Dejvida Gregorija i Isaka Njutna 1694. godine: Koliko najviše jediničnih sfera može istovremeno dodirivati datu sferu iste veličine?
Njutn je smatrao da je maksimalan broj 12 sfera, dok je Gregori verovao da je tačan odgovor 13. Međutim, nijedan nije imao dokaz za svoje tvrđenje, tako da su njihovi odgovori bili samo nagađanja. Čija intuicija je bila bolja, saznalo se 250 godina kasnije. Zahvaljujući ovoj diskusiji pomenuti problem se u literaturi često naziva Gregori-Njutnovim problemom.
Neka k(n) označava maksimalan broj n-dimenzionalnih sfera koje dodiruju datu sferu u n-dimenzionalnom prostoru, pri čemu su sve sfere jednake veličine. Tada je, očigledno, k(1)=2 i k(2)=6, kao što je prikazano na slici 2.
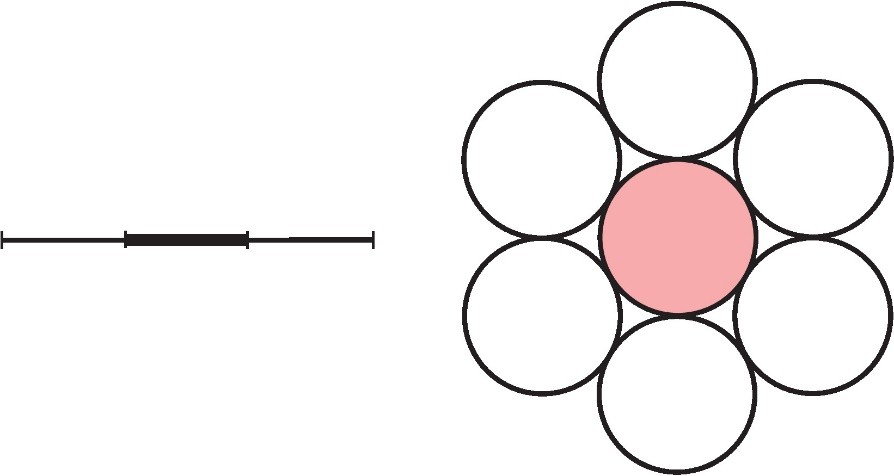
Sl. 2 Dodirujuće sfere u jedno i dvodimenzionalnom prostoru
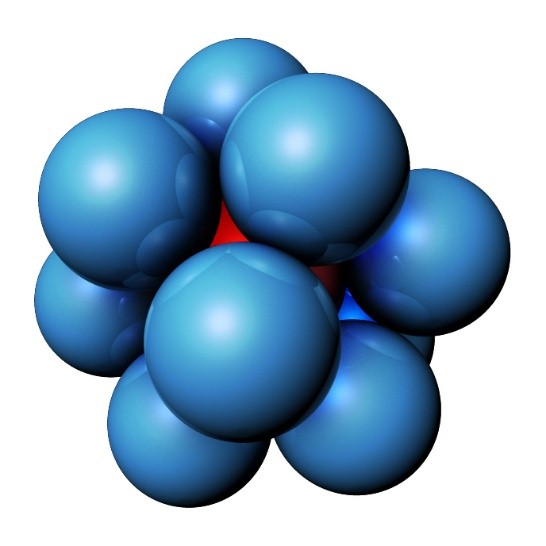
Sl. 3 Dodirujuće sfere u trodimenzionalnom prostoru
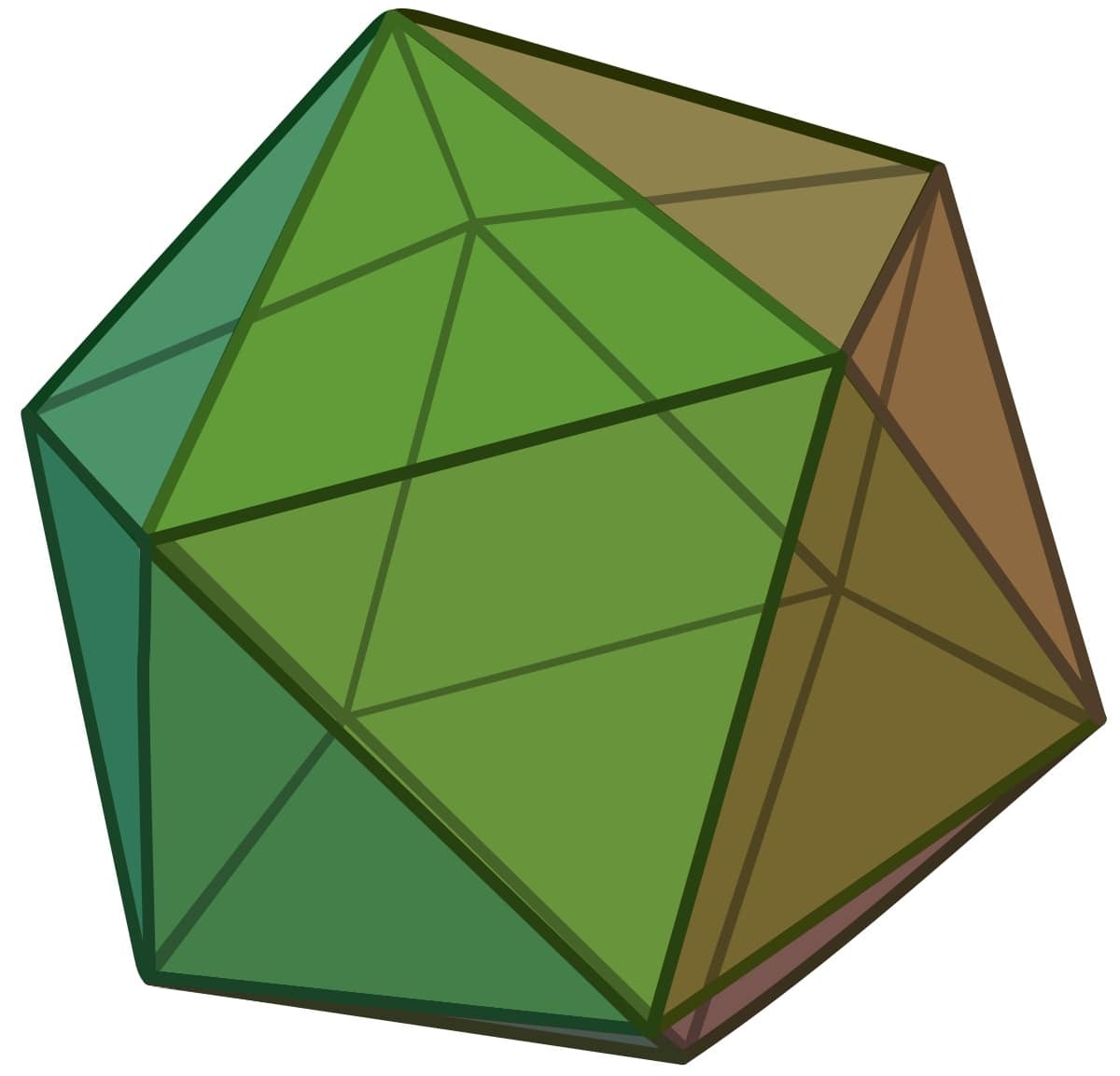
Sl. 4 Ikosaedar
U trodimenzionalnom prostoru moguće je rasporediti 12 sfera, tako da dodiruju datu sferu; na primer, dodirujuće sfere mogu se rasporediti u temenima pravilnog ikosaedra (ikosaedar je pravilni poliedar čije su strane jednakostranični trouglovi (ukupno 20) i ima 12 temena i 30 ivica), što se može videti na slici 4. Dejvid Gregori i mnogi drugi autori posle njega smatrali su da ova konfiguracija (kao i neke druge konfiguracije) ostavlja „dosta prostora” za trinaestu sferu. Dakle, k(3)=12 ili k(3)=13, koji je odgovor tačan?
Više od 250 godina ovaj problem je ostao nerešen, mada je bilo dato nekoliko „rešenja” u radovima i knjigama iz fizike. Konačno, problem su definitivno rešili Kurt Šitle i Bartel L. van der Varden 1953. godine.
Teorema. Ne više od 12 jediničnih sfera može se istovremeno rasporediti na takav način da svaka dodiruje datu sferu iste veličine.
Drugim rečima, k(3)=12. Ovo znači da je Njutnova intuicija bila ispravna mada za to nije imao dokaz. Tri godine posle Šitlea i Van der Vardena, Džon Lič dao je jednostavno rešenje, razumljivo relativno širokom krugu čitalaca; dovoljno je poznavanje nekih osnovnih elemenata iz sferne geometrije i teorije grafova. Njegov dokaz je sadržao neke sitne nekorektnosti, koje su kasnije drugi autori ispravili. Zainteresovani čitaoci mogu naći relativno jednostavno i kratko rešenje ruskog matematičara Olega Musina (koji živi u Los Anđelesu) na linku https://arxiv.org/pdf/math/0410324.pdf
Da li je moguće naći k(n) za neko n > 3 u n-dimenzionalnom prostoru? Prilično je iznenađujuće da je problem dodirujućih sfera rešen za vrlo visoke dimenzije 8 i 24; nađeno je k(8)=240 i k(24)=196560 (Endru Odlisko, Nejl Sloun i Vladimir Levenštajn, svi 1979.), ali je problem dugo ostao otvoren za dimenziju 4. Konačno, već pomenuti matematičar Oleg Musin pokazao je 2004. godine da je najveći broj dodirujućih sfera za dimenziju n=4 jednak 24.
U donjoj tabeli date su dosad pronađene vrednosti za k(n).
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
24 |
|
k(n) |
2 |
6 |
12 |
24 |
40 |
72 |
126 |
240 |
196560 |