Polimino, poznata i pod imenom super domina, jeste ravanska figura koja se sastoji od jediničnih kvadrata sastavljenih na različite načine preko zajedničkih ivica. Još od 1954, kada je matematičar Solomon Golomb lansirao polimino, ova vrsta ravanskih figura je postala svetski poznata zbog primene u zagonetkama-slagalicama, ali i u kombinatornoj geometriji.

Prof. Dr Miodrag Petković
Od svih slagalica sigurno je napoznatija (i najprodavanija ikada) video igra „tetris” koja je osvojila svet i našla svoje mesto u 185 država sveta. Iako postoje trdimenzionalne varijante, u ovom prilogu biće reči o dvodimenzionalnim problemima kojima su se bavili i svetski poznati matematičari i eksperti u računarskim naukama. Procenjuje se da je dosad na ovu temu napisano oko 300 naučnih radova i više hiljada stručnih članaka. Polimino problemi su veoma korisni ne samo za „gimnastiku mozga” za sve uzraste, već i za razvoj kognitivnih osobina najmlađih, što se praktikuje u većem delu sveta.
Polimino je ravanska figura koja se sastoji od jediničnih kvadrata (nazivaju se kompozitni kvadrati) sastavljenih na različite načine preko zajedničkih ivica. U slučaju pet kompozitnih kvadrata ove figure su prikazane na slici 1. Neki autori nazivaju polimono super dominom. Termin polimino prvi je uveo Solomon Golomb 1954. godine, dok je još bio asistent na Harvardskom univerzitetu. Na primer, svima dobro poznata domina je pravougaonik formiran od dva spojena kvadrata, tromino se sastoji od tri kvadrata, a tetramino se sastoji od četiri kvadrata.

Aleksej Pažitnov (Wikipedia)
Tetramino figure su 1984. godine iskorišćene za kreiranje veoma popularne igre za računare „tetris”. Autor je Aleksej Pažitnov (r. 1955.), tada zaposlen kao softverski inženjer u Institutu Sovjetske akademije nauka. Od prvih verzija za kućne personalne računare, ova igra je u kasnijim varijantama modifikovana za konzole za video-igre, plejere raznih vrsta, mobilne telefone i tablete i prodavana je u 185 zemalja sveta. Američki magazini za video igre proglasili su igru „tetris”, u različitim verzijama, „najvećom video igrom svih vremena”. Možda jeste a mozda i nije, rekli bi mlađi, ali ono što je sigurno jeste da je najprodavanija do današnjih dana: oko 520 miliona kopija (preuzeta kao aplikacija za PC i mobilne uređaje ili u obliku prenosivih elektronskih spravica).
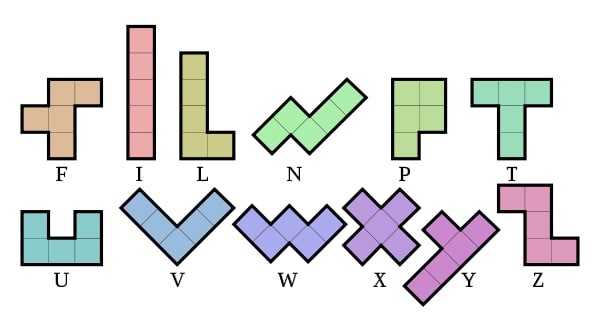
Sl. 1 Dvanaest figura pentamina
Za polimino figure vezan je jedan nerešen matematički problem koji se odnosi na broj različitih oblika P(n) polimino figura sastavljenih od n jediničnih kvadrata (izuzimajući oblike koji se dobijaju rotacijom ili refleksijom – kao likovi u ogledalu). Lako se nalazi P(1) = 1, P(2) = 1, P(3) = 2, P(4) = 5, P(5) = 12. Pomoću računara pronađeno je P(10) = 4.655, P(11) = 17.073 itd. Tomas Oliveira e Silva je 2007. tabelirao P (n) pomoću računara zaključno sa n = 28. Za sada su poznate grube granice za P (n) date sa
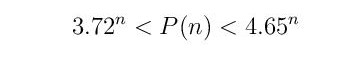
i to samo za dovoljno veliko n. Teorijski argumenti i numerički proračuni do izvesne mere daju procenu broja fiksnih polimina veličine n
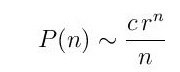
gde je r = 4,0626 i c = 0,3169, pri čemu su vrednosti r i c samo procene.
Osim domina, najširu popularnost imaju pentamino figure sastavljene preko zajedničkih stranica od pet jediničnih kvadrata. Ove figure najčešće su bile predmet raznovrsnih kombinatornih problema i igara na različitim tablama. Prve igre ovog tipa datiraju iz 1907. godine, ali su verovatno bile poznate i ranije. Opširno o ovome može se naći u knjizi Polyomineos (1965), čiji je autor već pomenuti Solomon Golomb, kasnije profesor Kalifornijskog univerziteta u Los Anđelesu (UCLA). Postoji tačno 12 različitih oblika pentamina koje zovemo kompletom pentamina. Ovih 12 pentamina se može efikasno, zbog sličnosti, predstaviti pomoću velikih slova latinice F, I, L, N, P, T, U, V, W, X, Y, Z (sl. 1).
Čuveni britanski matematičar Džon Horton Konvej predložio je alternativno označavanje figura pentamina koristići O umesto I, Q umesto L, R umesto F i S umesto N (sl. 2). Sličnost oblika figura sa slovima u ovom slučaju je malo isforsirana, ali ova šema obeležavanja ima prednost jer koristi 12 uzastopnih slova abecede. U ovom prilogu koristićemo način označavanja sa slike 1.
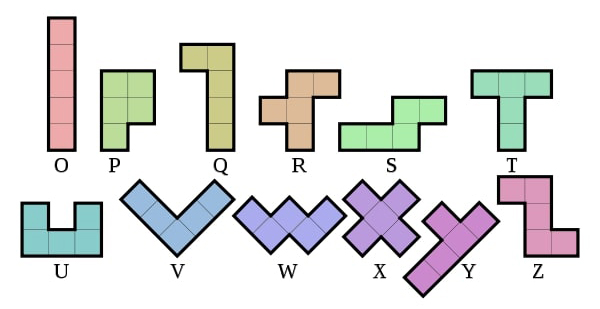
Sl. 2 Konvejev sistem označavanja pentamino figura
Postoji više igara sa figurama pentamina, od kojih je najpoznatija ona na šahovskoj tabli 8 x 8 koju dva igrača naizmenično „popločavaju” figurama pentamina (postoji i varijanta sa tri igrača). Igrač koji poslednji postavi svoju figuru je pobednik. Analizom 22 milijarde pozicija Hilari Orman je u radu objavljenom 1996. pokazala da igrač koji počinje igru uvek dobija. Vratimo se tetramino figurama i „tetrisu”, video igri-slagalici koju je kreirao sovjetski softverski inženjer Aleksej Pažitnov 1984. Tetramino figure koje učestvuju u ovoj igri prikazane su na slici 3.
Sl. 3 Tetramino figure koje
učestvuju u igri „tetris”
Pažitnov je dao ime svojoj igri kombinujući delove grčke reči tetra (što znači četiri) i reči tenis čiji je veliki ljubitelj. Kao državni službenik nije dobio nijednu rublju za svoj pronalazak prema zakonima tadašnjeg sovjetskog zakona da je svaki pronalazak vlasništvo države. Autorska prava dobio je tek 1996. godine u SAD gde je emigrirao s porodicom 1991. Mislim da ne treba objašnjavati pravila igre jer se mogu naći na internetu, a pored toga su suviše jednostavna. Svaka „srušena” linija se boduje (zavisno od nivoa igre) i na samom početku je postavljeno pitanje: „Da li bi bilo moguće igrati zauvek?”
Ovaj problem je prvi put razmatran u magistarskoj tezi Džona Brzustovskog 1992. godine, odbranjenoj na Univerzitetu Britanska Kolumbija. Zaključak je bio da statistički igra ima svoj kraj. Ako igraču počinje da se naizmenično javlja veći broj S i Z tetramina (oblik ovih figura prikazan je na sl. 3), „gravitacija” koju koristi standardna igra, igrač ne može izbeći „pukotine” koju stvaraju ova dva tetramina na tabli. Pukotine će se nužno nizati sve do vrha, a samim tim se linije ne mogi rušiti i na kraju će se igra završiti. Ovde svesno koristimo pogrešan termin linija mada je u pitanju pravougaonik formata 1 x 10 Postoje i verzije „tetrisa” sa širinom većom od 10.
Nije poznat najveći broj poena koji je čovek postigao, iz mnogo razloga nije moguće voditi takvu statistiku a proveravati rekorde jer je to skup posao bez imalo značaja. Bar do sada, poznato je da je najveći broj poena ostvaren korišćenjem veštačke inteligencije. Jubtjuber Greg Kenon smislio je specijalni algoritam StackRabbit postigao je 102 miliona poena (tačnije 102.252.920) na nivou 237 sa 3.112 „srušenih” linija.
U nastavku dajemo pet zanimljivih zadataka u kojima se kao glavni objekti javljaju polimino figure. Slova P i T ukazuju da se u zadatku koriste pentamino, odnosno tetramino figure. Neki od ovih zadataka pružiće čitaocima višenedeljno uživanje.
Zadatak P-1. Na koji način se od Y pentamina može sastaviti pravougaonik najmanje površine (tj. od minimalnog broja Y pentamina)?
Zadatak P-2. Koristeći komplet pentamina i jedan kvadratni tetramino (kvadrat 2 x 2) pokriti šahovsku tablu.
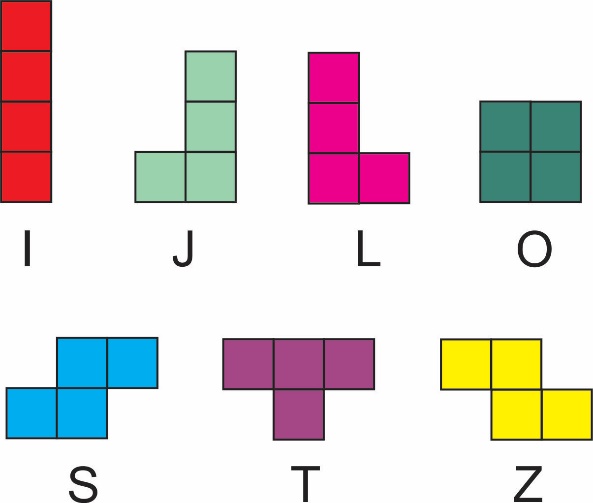
Zadatak P-3. Svaka figura pentamina ima površinu od 5 jediničnih kvadrata tako da se od kompleta pentamina može sastaviti pravougaonik dimenzije 6 x 10. Postoji veliki broj rešenja ovog zadatka do kojih je lako doći. Jedno rešenje je prikazano na slici 4. Međutim, zadatak postaje izazovan i težak ako se uvede sledeće ograničenje: Od kompleta pentamina sastaviti pravougaonik dimenzije 6 x 10 tako da svaka od 12 figura dodiruje graničnu ivicu pravougaonika.
Sl. 4 Pravougaonik 6 x 10 sastavljen od svih
figura pentamina
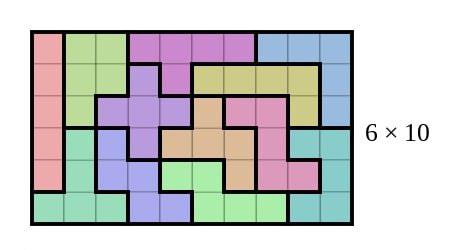
Zadatak T-4. Imamo 25 pločica L-tetramina oblika
od kojih je svaki sastavljen od 4 jedinična kvadrata. Da li je moguće potpuno pokriti (bez preklapanja) kvadratnu tablu 10 x 10 pomoću datog kompleta L-tetramina, pri čemu je dozvoljena rotacija tetramina za 90, 180 i 270 stepeni?
Pomenimo još jedan vrlo interesantan problem koji je u svoje vreme izazvao burnu diskusiju u časopisu Journal of Recreational Mathematics. U zadatku se koristi komplet pentamino figura prikazan na slikama 1 i 2. Zadatak je postavio Donald Knut, jedan od najvećih naučnika u računarskim naukama, dugogodišnji profesor Univerziteta u Stenfordu i dobitnik Tjuringove nagrade (najveće priznanje u kompjuterskim naukama) i član više nacionalnih akademija nauka. Dugogodišnja korespondencija sa profesorom Knutom na teme iz matematike, računarskih nauka i šaha bila je autoru ovog priloga posebna čast i zadovoljstvo.
Zadatak T-5. (D. Knut) Koristeći komplet od 12 pentamina napraviti ogradu bilo kog oblika koja će potpuno ograditi oblast maksimalne površine. Duž cele svoje dužine ograda mora imati širinu od bar jednog kompozitnog kvadrata 1 x 1, drugim rečima, figure se ne smeju spajati temenima već samo preko ivica.
U nastavku priloga dajemo rešenja postavljenih zadataka za čitaoce koji nisu uspeli da dođu do rešenja, od kojih su neka (mora se priznati) dosta teška.
Rešenje P-1: Najmanji pravougaonik koji se može sastaviti od Y-pentamina prikazan je na sl. 5. Postoje četiri različite šeme sastavljanja takvog pravougaonika.
Sl. 5 Pravougaonik minimalne
površine
Rešenje P-2: Jedno rešenje je
prikazano na sl. 6.

Sl. 6 Popločavanje šahovske table
Čuveni engleski kompozitor šahovskih (i drugih zanimljivih) problema i zagonetki T. R. Doson (Dawson) dokazao je da ovaj problem ima rešenje za proizvoljan položaj kvadratnog tetramina na šahovskoj tabli. Dejna Skot, matematičar sa Univerziteta Prinston, pomoću računara pronašao je 1958. godine 65 različitih rešenja (isključujući ona rešenja koja se dobijaju pomoću rotacije i refleksije) s kvadratom u centru table.
Rešenje P-3: Postoje samo dva rešenja, prikazana na slici 7.
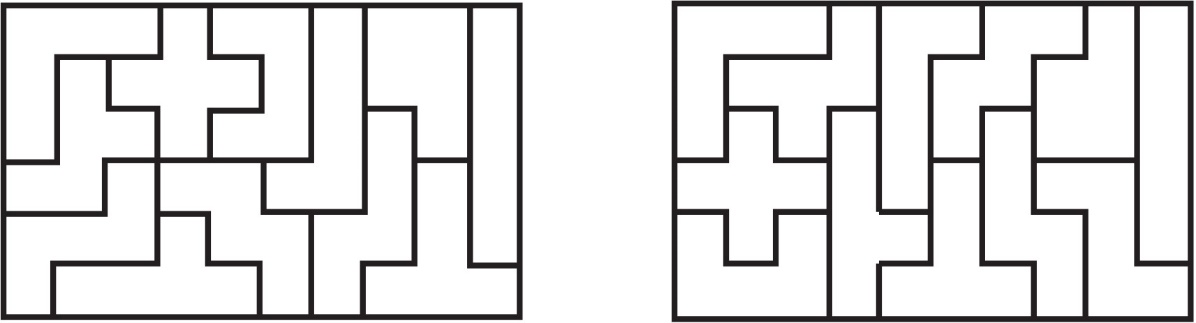
Sl. 7 Pravougaonik 6 x 10: svaka figura dodiruje graničnu ivicu pravougaonika
Rešenje T-4: Upišimo brojeve 1 i 5 u kvadrate table 10 x 10, kao što je prikazano na slici 8. Svaki L-tetramino pokriva ili tri jedinice i jednu peticu (suma brojeva iznosi 8) ili tri petice i jednu jedinicu (suma brojeva je 16), zavisno od orijentacije L-tetramina. Pretpostavimo da imamo x tetramina koji pokrivaju polja sa zbirom 16, tada 25–x tetramina pokriva polja sa zbirom 8. Suma brojeva na svim tetraminima jednaka je S’ = 16x + 8(25 – x) = 8x + 200. Suma brojeva na tabli je 300 i ako bi tabla mogla da se potpuno prekrije bez preklapanja onda jednačina 300 = 8x + 200 (=S’), odnosno 8x = 100 mora da ima celobrojno rešenje po x. Međutim, 100 nije deljivo sa 8 pa prema tome popločavanje nije moguće.

Sl. 8 Popločavanje table 10 x 10 pomoću L-tetramina
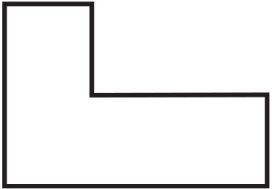
Rešenje T-5: Pentamino-ograda koja okružuje maksimalnu površinu od 128 jediničnih kvadrata prikazana je na slici 9. Rešenje je dao sam Donald Knut. Mada rešenje nije jedinstveno, on je pokazao da broj od 128 kvadratnih jedinica ne može biti nadmašen.

Sl. 9 Pentamino ograda najveće
površine








