Полимино, позната и под именом супер домина, јесте раванска фигура која се састоји од јединичних квадрата састављених на различите начине преко заједничких ивица. Још од 1954, када је математичар Соломон Голомб лансирао полимино, ова врста раванских фигура је постала светски позната због примене у загонеткама-слагалицама, али и у комбинаторној геометрији.

Проф. Др Миодраг Петковић
Од свих слагалица сигурно је напознатија (и најпродаванија икада) видео игра „тетрис” која је освојила свет и нашла своје место у 185 држава света. Иако постоје трдимензионалне варијанте, у овом прилогу биће речи о дводимензионалним проблемима којима су се бавили и светски познати математичари и експерти у рачунарским наукама. Процењује се да је досад на ову тему написано око 300 научних радова и више хиљада стручних чланака. Полимино проблеми су веома корисни не само за „гимнастику мозга” за све узрасте, већ и за развој когнитивних особина најмлађих, што се практикује у већем делу света.
Полимино је раванска фигура која се састоји од јединичних квадрата (називају се композитни квадрати) састављених на различите начине преко заједничких ивица. У случају пет композитних квадрата ове фигуре су приказане на слици 1. Неки аутори називају полимоно супер домином. Термин полимино први је увео Соломон Голомб 1954. године, док је још био асистент на Харвардском универзитету. На пример, свима добро позната домина је правоугаоник формиран од два спојена квадрата, тромино се састоји од три квадрата, а тетрамино се састоји од четири квадрата.

Алексеј Пажитнов (Wikipedia)
Тетрамино фигуре су 1984. године искоришћене за креирање веома популарне игре за рачунаре „тетрис”. Аутор је Алексеј Пажитнов (р. 1955.), тада запослен као софтверски инжењер у Институту Совјетске академије наука. Од првих верзија за кућне персоналне рачунаре, ова игра је у каснијим варијантама модификована за конзоле за видео-игре, плејере разних врста, мобилне телефоне и таблете и продавана је у 185 земаља света. Амерички магазини за видео игре прогласили су игру „тетрис”, у различитим верзијама, „највећом видео игром свих времена”. Можда јесте а мозда и није, рекли би млађи, али оно што је сигурно јесте да је најпродаванија до данашњих дана: око 520 милиона копија (преузета као апликација за PC и мобилне уређаје или у облику преносивих електронских справица).
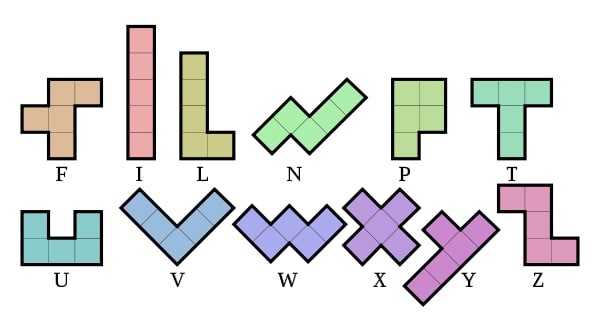
Сл. 1 Дванаест фигура пентамина
За полимино фигуре везан је један нерешен математички проблем који се односи на број различитих облика P(n) полимино фигура састављених од n јединичних квадрата (изузимајући облике који се добијају ротацијом или рефлексијом – као ликови у огледалу). Лако се налази P(1) = 1, P(2) = 1, P(3) = 2, P(4) = 5, P(5) = 12. Помоћу рачунара пронађено је P(10) = 4.655, P(11) = 17.073 итд. Томас Оливеира е Силва је 2007. табелирао P (n) помоћу рачунара закључно са n = 28. За сада су познате грубе границе за P (n) дате са
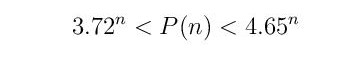
и то само за довољно велико н. Теоријски аргументи и нумерички прорачуни до извесне мере дају процену броја фиксних полимина величине n
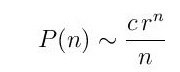
где је r = 4,0626 и c = 0,3169, при чему су вредности r и c само процене.
Осим домина, најширу популарност имају пентамино фигуре састављене преко заједничких страница од пет јединичних квадрата. Ове фигуре најчешће су биле предмет разноврсних комбинаторних проблема и игара на различитим таблама. Прве игре овог типа датирају из 1907. године, али су вероватно биле познате и раније. Опширно о овоме може се наћи у књизи Polyomineos (1965), чији је аутор већ поменути Соломон Голомб, касније професор Kалифорнијског универзитета у Лос Анђелесу (UCLA). Постоји тачно 12 различитих облика пентамина које зовемо комплетом пентамина. Ових 12 пентамина се може ефикасно, због сличности, представити помоћу великих слова латинице F, I, L, N, P, T, U, V, W, X, Y, Z (сл. 1).
Чувени британски математичар Џон Хортон Kонвеј предложио је алтернативно означавање фигура пентамина користићи O уместо I, Q уместо L, R уместо F i S уместо N (сл. 2). Сличност облика фигура са словима у овом случају је мало исфорсирана, али ова шема обележавања има предност јер користи 12 узастопних слова абецеде. У овом прилогу користићемо начин означавања са слике 1.
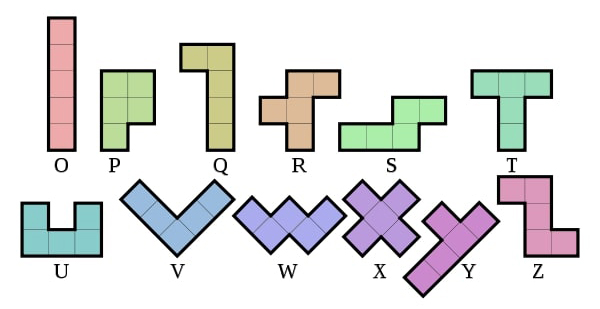
Сл. 2 Kонвејев систем означавања пентамино фигура
Постоји више игара са фигурама пентамина, од којих је најпознатија она на шаховској табли 8 x 8 коју два играча наизменично „поплочавају” фигурама пентамина (постоји и варијанта са три играча). Играч који последњи постави своју фигуру је победник. Анализом 22 милијарде позиција Хилари Орман је у раду објављеном 1996. показала да играч који почиње игру увек добија. Вратимо се тетраминo фигурама и „тетрису”, видео игри-слагалици коју је креирао совјетски софтверски инжењер Алексеј Пажитнов 1984. Тетрамино фигуре које учествују у овој игри приказане су на слици 3.
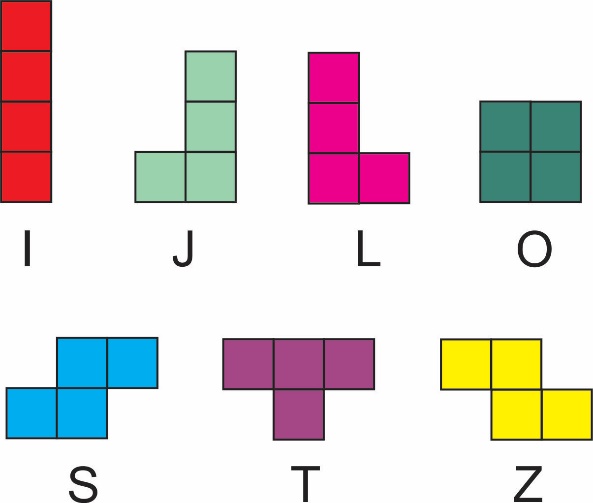
Сл. 3 Тетрамино фигуре које
учествују у игри „тетрис”
Пажитнов је дао име својој игри комбинујући делове грчке речи тетра (што значи четири) и речи тенис чији је велики љубитељ. Kао државни службеник није добио ниједну рубљу за свој проналазак према законима тадашњег совјетског закона да је сваки проналазак власништво државе. Ауторска права добио је тек 1996. године у САД где је емигрирао с породицом 1991. Мислим да не треба објашњавати правила игре јер се могу наћи на интернету, а поред тога су сувише једноставна. Свака „срушена” линија се бодује (зависно од нивоа игре) и на самом почетку је постављено питање: „Да ли би било могуће играти заувек?”
Овај проблем је први пут разматран у магистарској тези Џона Брзустовског 1992. године, одбрањеној на Универзитету Британска Kолумбија. Закључак је био да статистички игра има свој крај. Ако играчу почиње да се наизменично јавља већи број S и Z тетрамина (облик ових фигура приказан је на сл. 3), „гравитација” коју користи стандардна игра, играч не може избећи „пукотине” коју стварају ова два тетрамина на табли. Пукотине ће се нужно низати све до врха, а самим тим се линије не моги рушити и на крају ће се игра завршити. Овде свесно користимо погрешан термин линија мада је у питању правоугаоник формата 1 x 10 Постоје и верзије „тетриса” са ширином већом од 10.
Није познат највећи број поена који је човек постигао, из много разлога није могуће водити такву статистику а проверавати рекорде јер је то скуп посао без имало значаја. Бар до сада, познато је да је највећи број поена остварен коришћењем вештачке интелигенције. Јубтјубер Грег Kенон смислио је специјални алгоритам StackRabbit постигао је 102 милиона поена (тачније 102.252.920) на нивоу 237 са 3.112 „срушених” линија.
У наставку дајемо пет занимљивих задатака у којима се као главни објекти јављају полимино фигуре. Слова P и Т указују да се у задатку користе пентамино, односно тетрамино фигуре. Неки од ових задатака пружиће читаоцима вишенедељно уживање.
Задатак P-1. На који начин се од Y пентамина може саставити правоугаоник најмање површине (тј. од минималног броја Y пентамина)?
Задатак P-2. Kористећи комплет пентамина и један квадратни тетрамино (квадрат 2 x 2) покрити шаховску таблу.
Задатак P-3. Свака фигура пентамина има површину од 5 јединичних квадрата тако да се од комплета пентамина може саставити правоугаоник димензије 6 x 10. Постоји велики број решења овог задатка до којих је лако доћи. Једно решење је приказано на слици 4. Међутим, задатак постаје изазован и тежак ако се уведе следеће ограничење: Од комплета пентамина саставити правоугаоник димензије 6 x 10 тако да свака од 12 фигура додирује граничну ивицу правоугаоника.
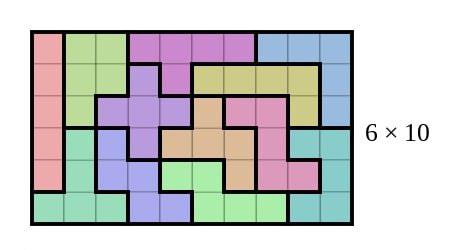
Сл. 4 Правоугаоник 6 x 10 састављен од свих
фигура пентамина
Задатак Т-4. Имамо 25 плочица L-тетрамина облика
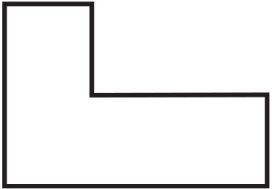
од којих је сваки састављен од 4 јединична квадрата. Да ли је могуће потпуно покрити (без преклапања) квадратну таблу 10 x 10 помоћу датог комплета L-тетрамина, при чему је дозвољена ротација тетрамина за 90, 180 и 270 степени?
Поменимо још један врло интересантан проблем који је у своје време изазвао бурну дискусију у часопису Journal of Recreational Mathematics. У задатку се користи комплет пентамино фигура приказан на сликама 1 и 2. Задатак је поставио Доналд Kнут, један од највећих научника у рачунарским наукама, дугогодишњи професор Универзитета у Стенфорду и добитник Тјурингове награде (највеће признање у компјутерским наукама) и члан више националних академија наука. Дугогодишња кореспонденција са професором Kнутом на теме из математике, рачунарских наука и шаха била је аутору овог прилога посебна част и задовољство.
Задатак Т-5. (Д. Kнут) Kористећи комплет од 12 пентамина направити ограду било ког облика која ће потпуно оградити област максималне површине. Дуж целе своје дужине ограда мора имати ширину од бар једног композитног квадрата 1 x 1, другим речима, фигуре се не смеју спајати теменима већ само преко ивица.
У наставку прилога дајемо решења постављених задатака за читаоце који нису успели да дођу до решења, од којих су нека (мора се признати) доста тешка.
Решење P-1: Најмањи правоугаоник који се може саставити од Y-пентамина приказан је на сл. 5. Постоје четири различите шеме састављања таквог правоугаоника.
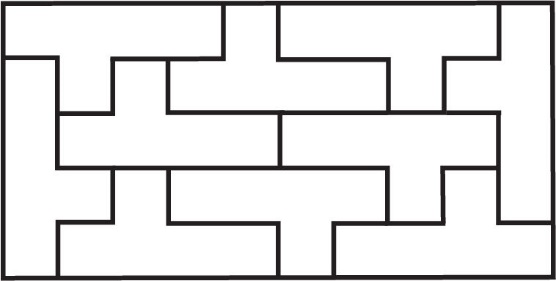
Сл. 5 Правоугаоник минималне
површине
Решење P-2: Једно решење је
приказано на сл. 6.

Сл. 6 Поплочавање шаховске табле
Чувени енглески композитор шаховских (и других занимљивих) проблема и загонетки Т. Р. Досон (Dawson) доказао је да овај проблем има решење за произвољан положај квадратног тетрамина на шаховској табли. Дејна Скот, математичар са Универзитета Принстон, помоћу рачунара пронашао је 1958. године 65 различитих решења (искључујући она решења која се добијају помоћу ротације и рефлексије) с квадратом у центру табле.
Решење P-3: Постоје само два решења, приказана на слици 7.
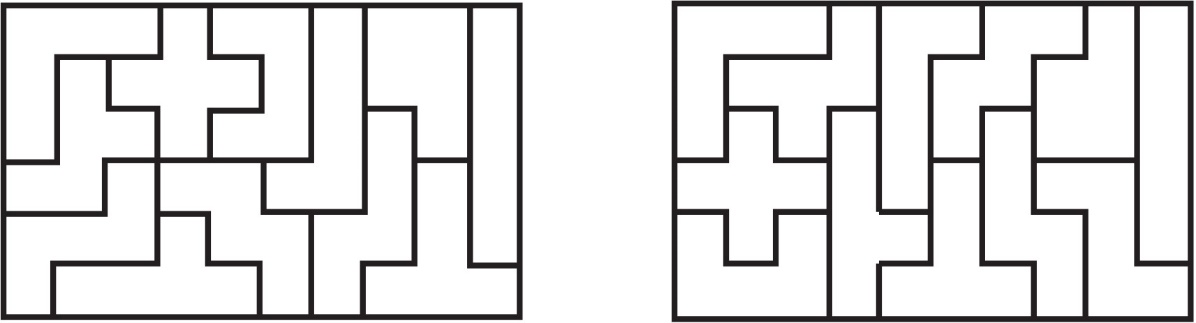
Сл. 7 Правоугаоник 6 x 10: свака фигура додирује граничну ивицу правоугаоника
Решење Т-4: Упишимо бројеве 1 и 5 у квадрате табле 10 x 10, као што је приказано на слици 8. Сваки L-тетрамино покрива или три јединице и једну петицу (сума бројева износи 8) или три петице и једну јединицу (сума бројева је 16), зависно од оријентације L-тетрамина. Претпоставимо да имамо x тетрамина који покривају поља са збиром 16, тада 25–x тетрамина покрива поља са збиром 8. Сума бројева на свим тетраминима једнака је S’ = 16x + 8(25 – x) = 8x + 200. Сума бројева на табли је 300 и ако би табла могла да се потпуно прекрије без преклапања онда једначина 300 = 8x + 200 (=S’), odnosno 8x = 100 мора да има целобројно решење по x. Међутим, 100 није дељиво са 8 па према томе поплочавање није могуће.

Сл. 8 Поплочавање табле 10 x 10 помоћу L-тетрамина
Решење Т-5: Пентамино-ограда која окружује максималну површину од 128 јединичних квадрата приказана је на слици 9. Решење је дао сам Доналд Kнут. Мада решење није јединствено, он је показао да број од 128 квадратних јединица не може бити надмашен.

Сл. 9 Пентамино ограда највеће
површине








