Često se neki problemi iz raznih disciplina svode na to da se u rešavanje uključuju matematičari. U ovom prilogu biće predstavljena dva iste vrste iz građevinskih konstrukcija i fizike. Oba su dovoljno intrigantna da za široku publiku, a više decenija predstavljaju tvrd orah za rešavače.

Prof. dr Miodrag Petković
Naslov priloga je mala šala, mada ništa nije nemoguće: kada nema posla zašto i matematičari ne bi čuvali muzeje. Jedino bi možda postojao rizik da takav čuvar iz dosade uradi nešto slično kao onaj u ruskom gradu Jekaterinburgu. On je, naime, na „prazna” lica dve osobe na slici koja pripada modernom slikarstvu hemijskom olovkom docrtao oči. Izgubio je posao, oduzet mu je alat za slikanje i osuđen je na tri meseca zatvora. Valjda je to bio jedan od razloga zašto je Pikaso na svojim slikama (recimo „Gospođice iz Avinjona”) preventivno crtao oči na licima ljudi.
U nastavku je opisan obiljniji pristup u vezi s galerijama i sličnim cik-cak objektima. Mada je geometrijski oblik pomenutih objekata često veoma komplikovan i čini vrlo čudne ornamente (videti, na primer, sliku 1), aproksimativno se može uzeti da ravanski presek ima oblik mnogougla. Ako galerija ima zidove, normalno se postavlja sledeće nimalo lako pitanje: Koliki je najmanji broj čuvara koji mogu potpuno da kontrolišu celokupan prostor galerije (označene sa G’ na slici 1)?
Rešenje ovog problema dao je Vašek Hvatal (1946- ), češko-američki profesor računarskih nauka i matematike na Univerzitetu Mekgil u Montrealu (Kanada), sada profesor emeritus, koristeći svoju teoremu iz oblasti triangulacije (premeravanje zemljišta ili drugih planarnih površina pomoću međusobno povezanih troglova). On je dokazao da, ako galerija ima n zidova (tj. ako obrazuje poligon sa n strana), tada je minimalan broj čuvara koji mogu da nadziru celu galeriju jednak ⌊n/3⌋, gde simbol ⌊·⌋ označava najveći celobrojni deo od n/3. Na primer, ⌊4⌋ = 4, ⌊6.9⌋ = 6, ⌊9.01⌋ = 9. Za galeriju sa slike 1, gde je n = 43, potreban broj čuvara je ⌊43/3⌋ = ⌊14.333…⌋ = 14.
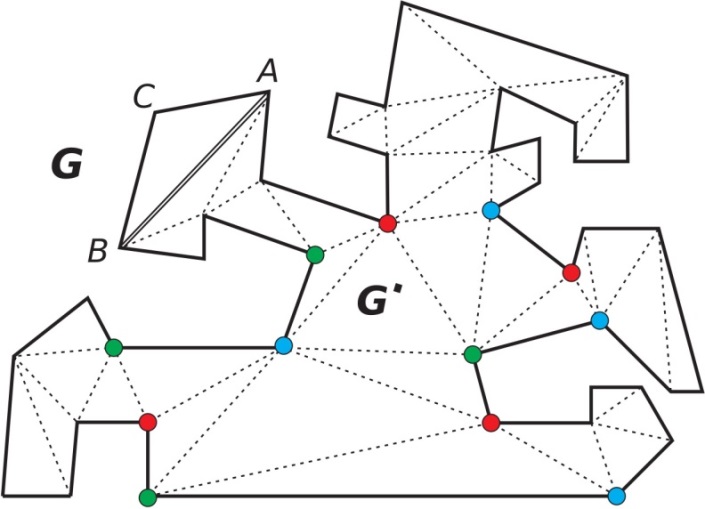
Sl. 1 Triangulacija galerije, n = 43
Ovde navodimo jedan interesantan dokaz Hvatalove teoreme dat u 5. poglavlju knjige Mathematical Gardner (editor A. A. Klarner, 1981), posvećene velikom popularizatoru matematike Martinu Gardneru (1914-2010). Kao što je napomenuto, galeriju od n strana smatraćemo n-touglom. Ovaj n-tougao može se podeliti na trouglove pomoću nepresecajućih dijagonala koje spajaju njegova temena (tzv. triangulacija, videti sliku 1). Obojimo temena dobijenog grafa tako da temena koja pripadaju istoj duži budu obojena različitim bojama. Koristeći metod matematičke indukcije pokazaćemo, najpre, da su za ovo bojenje dovoljne tri boje.
Prvo, ako je n = 3 galerija ima oblik trougla i za bojenje njegovih temena su dovoljne tri boje. Pretpostavimo sada da su tri boje takođe dovoljne za pravilno bojenje temena trianguliranog n-tougla G’ (n je najmanje 3). Posmatrajmo mnogougao G sa (n+1)-stranom koji se dobija iz G’ tako što se umesto strane (zida galerije) AB posmatraju pridodate strane (zidovi) AC i CB. Po induktivnoj pretpostavci temena trianguliranog n-tougla G’ su obojena pomoću tri boje. Temena A i B leže na istoj duži tako da su obojena različitim bojama. Ako teme C trougla ABC obojimo trećom bojom proizilazi da je i mnogougao G sa (n+1)-stranom moguće obojiti pomoću tri boje. Prema tome, temena svakog trianguliranog n-tougla mogu se obojiti pomoću tri različite boje a, b i c tako da međusobno povezana temena budu obojena različitim bojama.
Neka Na, Nb i Nc označavaju broj temena obojenih redom bojama a, b i c. Ako je n broj strana trianguliranog mnogougla, lako je videti da razlika između brojeva Na, Nb i Nc iznosi ili 1 ili 0. U slučaju da je n deljivo sa 3, tada je Na = Nb = Nc = n/3; u suprotnom ovi brojevi pripadaju skupu
{⌊n/3⌋+1, ⌊n/3⌋}. Prema tome, minimalan broj temena u jednoj boji je ⌊n/3⌋. Ako u svako od ovih temena postavimo čuvare, oni će kontrolisati svaki od trouglova na koje je podeljen n-tougao, što znači da kontrolišu i celu galeriju.
Kad smo već kod prostorija čiji preseci imaju oblik mnogougla, vredno je pomenuti jedan interesantan problem pod nazivom bilijarska „crna rupa” koji pripada oblasti fizike, ali i matematike. Matematičarima padaju na pamet razne čudnovate ideje, a pritom im pomažu fizičari i astronomi koji su već decenijama opsednuti „crnim rupama” u kosmosu.
Pedesetih godina dvadesetog veka nemačko-američki matematičar Ernst Štraus postavio je sledeće pitanje: Da li je moguće napraviti sobu čiji su zidovi prekriveni ogledalima tako da svetlost iz jedne (pogodno izabrane) tačke ne može dopreti u sve tačke unutar sobe uzimajući u obzir da osvetljenje može dolaziti i posle refleksije od jednog ili više ogledala?
Problem je ekvivalentan sledećem bilijarskom problemu: Da li se može konstruisati takav bilijarski sto da kugla udarena u nekoj (povoljno izabranoj) tački A nikad ne dođe u tačku B (tzv. crna rupa), makar se i beskonačno puta odbila od zidova (slika 2)? Ovaj zadatak nije bio nerešen sve do 1995. kada je Džordž Tokarski smislio sobu sa 26 zidova sa „crnom rupom”. Dve godine kasnije David Kastro i pomenuti DŽ. Tokarski su nezavisno jedan od drugog pokazali da je moguće konstruisati sobu sa 24 zida prikazanu na slici 2. Ako se sveća stavi u tačku A, osoba koja stoji u tački B neće videti svetlost uprkos refleksije sa staklenih ogledala postavljenih na zidove.
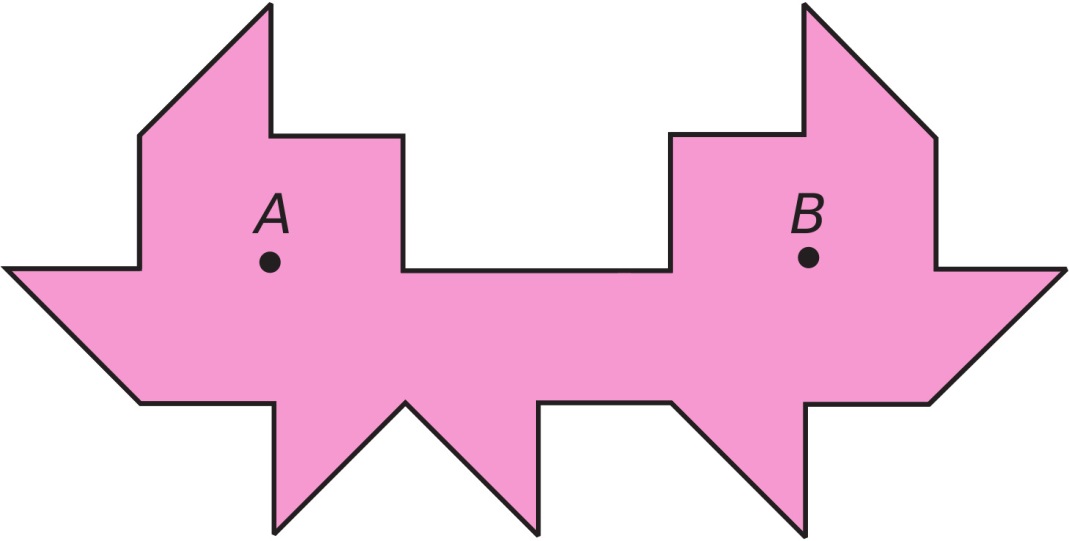
Sl. 2 Prostorija sa ,,crnom rupom”
Dodajmo na kraju da su 2016. Godine Lelier, Montej i Vajs dokazali da će svetlosni izvor u poligonijalnoj sobi čiji su svi uglovi (u stepenima) izraženi racionalnim brojevima osvetliti ceo poligon sa mogućim izuzetkom konačnog broja tačaka. I tako, od jednostavnih svakodnevnih stvari može se stići do naučnih problema koji zahtevaju decenije rada na rešavanju.








