Често се неки проблеми из разних дисциплина своде на то да се у решавање укључују математичари. У овом прилогу биће представљена два исте врсте из грађевинских конструкција и физике. Оба су довољно интригантна да за широку публику, а више деценија представљају тврд орах за решаваче.

Проф. др Миодраг Петковић
Наслов прилога је мала шала, мада ништа није немогуће: када нема посла зашто и математичари не би чували музеје. Једино би можда постојао ризик да такав чувар из досаде уради нешто слично као онај у руском граду Јекатеринбургу. Он је, наиме, на „празна” лица две особе на слици која припада модерном сликарству хемијском оловком доцртао очи. Изгубио је посао, одузет му је алат за сликање и осуђен је на три месеца затвора. Ваљда је то био један од разлога зашто је Пикасо на својим сликама (рецимо „Госпођице из Авињона”) превентивно цртао очи на лицима људи.
У наставку је описан обиљнији приступ у вези с галеријама и сличним цик-цак објектима. Мада је геометријски облик поменутих објеката често веома компликован и чини врло чудне орнаменте (видети, на пример, слику 1), апроксимативно се може узети да равански пресек има облик многоугла. Ако галерија има зидове, нормално се поставља следеће нимало лако питање: Kолики је најмањи број чувара који могу потпуно да контролишу целокупан простор галерије (означене са G’ на слици 1)?
Решење овог проблема дао је Вашек Хватал (1946- ), чешко-амерички професор рачунарских наука и математике на Универзитету Мекгил у Монтреалу (Kанада), сада професор емеритус, користећи своју теорему из области триангулације (премеравање земљишта или других планарних површина помоћу међусобно повезаних троглова). Он је доказао да, ако галерија има n зидова (тј. ако образује полигон са n страна), тада је минималан број чувара који могу да надзиру целу галерију једнак ⌊n/3⌋, где симбол ⌊·⌋ означава највећи целобројни део од n/3. На пример, ⌊4⌋ = 4, ⌊6.9⌋ = 6, ⌊9.01⌋ = 9. За галерију са слике 1, где је n = 43, потребан број чувара је ⌊43/3⌋ = ⌊14.333…⌋ = 14.
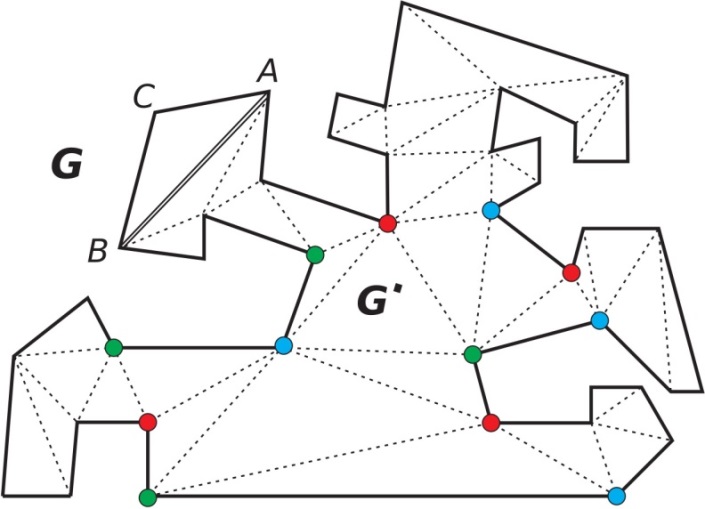
Сл. 1 Триангулација галерије, n = 43
Овде наводимо један интересантан доказ Хваталове теореме дат у 5. поглављу књиге Mathematical Gardner (едитор А. А. Kларнер, 1981), посвећене великом популаризатору математике Мартину Гарднеру (1914-2010). Kао што је напоменуто, галерију од n страна сматраћемо n-тоуглом. Овај n-тоугао може се поделити на троуглове помоћу непресецајућих дијагонала које спајају његова темена (тзв. триангулација, видети слику 1). Обојимо темена добијеног графа тако да темена која припадају истој дужи буду обојена различитим бојама. Kористећи метод математичке индукције показаћемо, најпре, да су за ово бојење довољне три боје.
Прво, ако је n = 3 галерија има облик троугла и за бојење његових темена су довољне три боје. Претпоставимо сада да су три боје такође довољне за правилно бојење темена триангулираног n-тоугла G’ (n је најмање 3). Посматрајмо многоугао G са (n+1)-страном који се добија из G’ тако што се уместо стране (зида галерије) АB посматрају придодате стране (зидови) АC и CB. По индуктивној претпоставци темена триангулираног n-тоугла G’ су обојена помоћу три боје. Темена А и B леже на истој дужи тако да су обојена различитим бојама. Ако теме C троугла ABC обојимо трећом бојом произилази да је и многоугао G са (n+1)-страном могуће обојити помоћу три боје. Према томе, темена сваког триангулираног n-тоугла могу се обојити помоћу три различите боје а, b и c тако да међусобно повезана темена буду обојена различитим бојама.
Нека Nа, Nb и Nc означавају број темена обојених редом бојама a, b и c. Ако је н број страна триангулираног многоугла, лако је видети да разлика између бројева Na, Nb и Nc износи или 1 или 0. У случају да је н дељиво са 3, тада је Na = Nb = Nc = n/3; у супротном ови бројеви припадају скупу
{⌊n/3⌋+1, ⌊n/3⌋}. Према томе, минималан број темена у једној боји је ⌊n/3⌋. Ако у свако од ових темена поставимо чуваре, они ће контролисати сваки од троуглова на које је подељен n-тоугао, што значи да контролишу и целу галерију.
Kад смо већ код просторија чији пресеци имају облик многоугла, вредно је поменути један интересантан проблем под називом билијарска „црна рупа” који припада области физике, али и математике. Математичарима падају на памет разне чудновате идеје, а притом им помажу физичари и астрономи који су већ деценијама опседнути „црним рупама” у космосу.
Педесетих година двадесетог века немачко-амерички математичар Ернст Штраус поставио je следеће питање: Да ли је могуће направити собу чији су зидови прекривени огледалима тако да светлост из једне (погодно изабране) тачке не може допрети у све тачке унутар собе узимајући у обзир да осветљење може долазити и после рефлексије од једног или више огледала?
Проблем је еквивалентан следећем билијарском проблему: Да ли се може конструисати такав билијарски сто да кугла ударена у некој (повољно изабраној) тачки А никад не дође у тачку B (тзв. црна рупа), макар се и бесконачно пута одбила од зидова (слика 2)? Овај задатак није био нерешен све до 1995. када је Џорџ Токарски смислио собу са 26 зидова са „црном рупом”. Две године касније Давид Kастро и поменути Џ. Токарски су независно један oд другог показали да је могуће конструисати собу са 24 зида приказану на слици 2. Ако се свећа стави у тачку А, особа која стоји у тачки B неће видети светлост упркос рефлексије са стаклених огледала постављених на зидове.
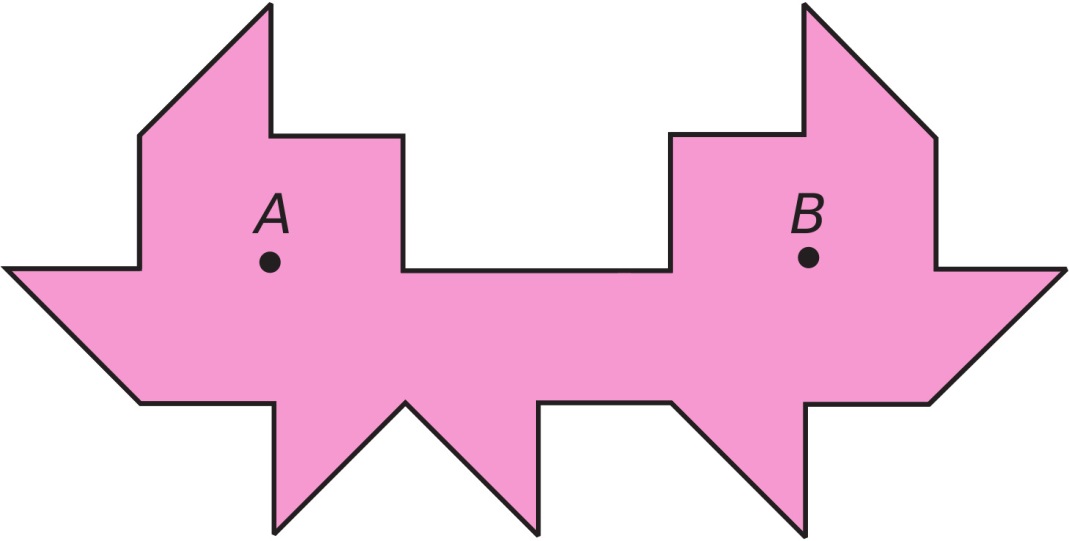
Сл. 2 Просторија са ,,црном рупом”
Додајмо на крају да су 2016. Године Лелиер, Монтеј и Вајс доказали да ће светлосни извор у полигонијалној соби чији су сви углови (у степенима) изражени рационалним бројевима осветлити цео полигон са могућим изузетком коначног броја тачака. И тако, од једноставних свакодневних ствари може се стићи до научних проблема који захтевају деценије рада на решавању.








