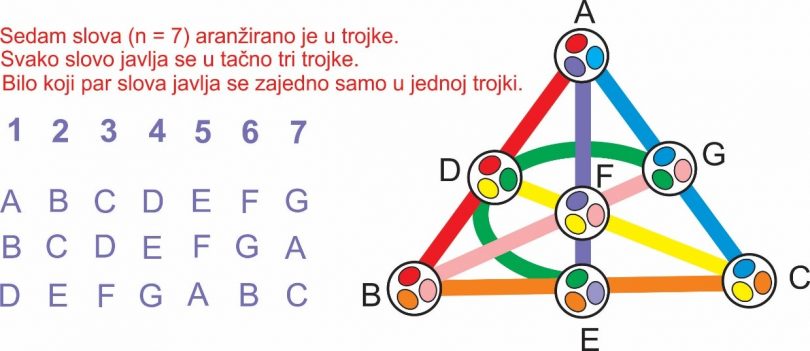
Na bojnom polju 16 ruskih vojnika opkolilo je 12 turskih vojnika. Svaki ruski vojnik je pucao samo jednom i svaki metak je prošao kroz turbane tri turska vojnika. Koliko turskih vojnika ima neprobušene turbane? I kakve to veze ima s matematičkim problemom Štajnerovih trojki, slikovito prikazanim u naslovnoj ilustraciji?

Prof. dr Miodrag Petković
Kirkmanov problem iz 19. veka o 15 učenica koje šetaju u trojkama i slični problem rekreativne matematike doveli su do razvoja jedne važne oblasti kombinatorike zvane blok-dizajn. Ispostavilo da su ovi problemi blisko povezani sa različitim naučnim disciplinama, kao što su statistika, teorija kodova, balansirani blok dizajni, konačna geometrija, Vajerštrasove eliptičke funkcije, kubne krive, Štajner-Kirkmanovi sistemi trojki, Adamarove matrice, projektivne ravni. To je i tema ovog priloga koji sadrži nekoliko interesantnih zadataka što imaju i praktičnu vrednost.
Godine 1850. Tomas Kirkman (1806-1895), engleski sveštenik a takođe ekspert u teoriji grupa i kombinatorici i član Kraljevskog društva, postavio je u časopisu Cambridge and Dublin Mathematical Journal (Vol. 2, str. 191-204) sledeći problem: Petnaest učenica svakog dana ide u šetnju grupisane u trojke. Napraviti takav raspored trojki da u sedam uzastopnih dana svaki par učenica prošeta zajedno jednom i samo jednom. Drugim rečima, svaka devojka u toku sedmice treba da prošeta sa svim svojim drugaricama, ali sa svakom samo jednom zajedno u trojci.
Pomenimo da je Kirkman formulisao ovaj problem rešavajući zadatak koji je postavio Vesli Vulhauz 1844. u okviru nagradnog takmičenja (objavljen u periodičnom magazinu Lady’s and Gentlemen’s Diary. Kirkman je rešio Vulhauzov zadatak 1847. i reformulisao ga 1850. kao problem učenica (The schoolgirl problem) u formi koja je gore navedena. Ovaj problem i slični, koji pripadaju oblasti kombinatorike zvanoj blok-dizajn, intenzivno su izučavani u 19. veku, ali uglavnom kao rekreativna matematika. Kasnije se ispostavilo da su blisko povezani sa različitim naučnim disciplinama, kao što su statistika, teorija kodova, balansirani blok dizajni, konačna geometrija, Vajerštrasove eliptičke funkcije, krive trećeg reda, Kirkman-Štajnerove trojke, Adamarove matrice, projektivne ravni.
Zagonetka sa učenicama koje šetaju ima svoju predistoriju u priči o farmeru koji želi da zasadi izvestan broj stabala u voćnjaku tako da postoji r pravih linija sa tačno k stabala u svakoj. Zadatak postaje težak ako se zahteva maksimalan broj redova (za zadati broj stabala n i k). Za n = 15 i k = 3 ovaj zadatak se svodi na Kirkmanov problem „15 učenica u šetnji”.
Generalizacija Kirkmanovog problema vodi do Štajnerovog sistema trojki, nazvanih tako prema radovima čuvenog švajcarskog matematičara Jakoba Štajnera (1796-1863). Štajnerov sistem Sn(k), ako postoji, jeste raspored n objekata po trojkama tako da se bilo koji par objekata javlja samo jednom u trojci. Postoji n(n-1)/2 parova i n(n-1)/6 trojki u Štajnerovom sistemu; odavde, n mora da bude kongruentno sa 1 ili 3 po modulu 6, to jest n = 7,9,13,15… E. H. Mur (Moore) je dokazao 1893. da je ovaj uslov takođe dovoljan. Podsećamo da se za cele brojeve a i b kaže da su kongruentni po modulu m (m je ceo broj različit od 0) ako a i b pri deljenju sa m daju jednake ostatke.

Tomas Kirkman, Jakob Štajner (Wikipedia)
U Kirkmanovom uopštenom problemu broj dana potreban za šetnje je (n-1)/2. Ovaj broj će biti ceo jedino ako je n neparan umnožak broja 3, tj. ako je oblika 3(2k+1) = 6m+3. Odavde dobijamo niz mogućih vrednosti 3, 9, 15, 21, itd. Pomenuti oblik 6m+3 je potreban za rešenje Kirkmanovog uopštenog problema, ali to nije dovoljno. U drugoj polovini 19. veka napisani su mnogobrojni naučni radovi na temu Kirkmanovog uopštenog problema, ali s rešenjima samo za pojedinačne slučajeve n. Generalno rešenje za proizvoljno n (oblika 6m+3) dali su 1971. godine D. K. Rej-Čauduri i Ričard M. Vilson sa Državnog univerziteta Ohajo. Interesantno je napomenuti da je kasnije ustavljeno da je pre 1971. rešenje dao školski učitelj Lu Ksia Ksi iz Mongolije, ali dokaz nije nigde publikovan tako da nije ni verifikovan. Međutim, broj bazičnih Štajnerovih trojki Sn u generalnom slučaju je ostao nepoznat i dan-danas i nađen je jedino za male vrednosti broja n. Sn raste veoma brzo: na primer, za n = 31 postoji više od bazičnih rešenja.
Slučaj n = 3 je trivijalan, tri devojke jednostavno šetaju u trojci samo jedan dan. Slučaj n = 9 devojaka u četvorodnevnoj šetnji ima jedinstveno osnovno rešenje dato u donjoj šemi:
123 147 159 168
456 258 267 249
789 369 348 357
Još 1922. godine bilo je poznato da Kirkmanov problem 15 učenica ima 80 rešenja, od kojih 7 bazičnih. Postoji više metoda pomoću kojih je moguće odrediti ova rešenja. Ovde ćemo izložiti jedan interesantan geometrijski pristup koji kombinuje fiksni i rotirajući disk iste veličine. Ovaj metod opisao je Martin Gardner u časopisu Scientific American (No 5, 1980).
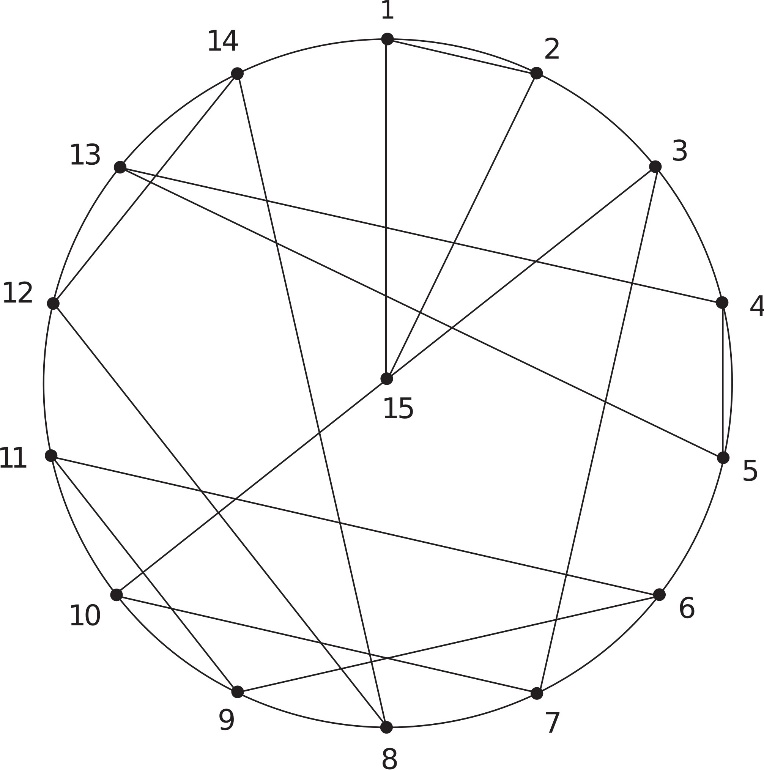
Sl. 1 Geometrijsko rešenje Kirkmanovog problema o šetnji 15 učenica
Nacrtajmo kružni disk i označimo na kružnici 14 pođednako udaljenih tačaka obeleženih brojevima od 1 do 14. Isecimo od kartona kružni disk iste veličine i označimo obod na isti način brojevima od 1 do 14, a centar brojem 15. Nacrtajmo, zatim, prečnik (10,15,3) i pet nepodudarnih trouglova (1, 2, 15), (3, 7, 10), (4, 5, 13), (6, 9, 11), (8, 12, 14), kao što je prikazano na slici 1. Naznačeni trouglovi, u stvari, predstavljaju (različite) tražene trojke i zbog toga ne smeju biti podudarni između sebe. Moguće je napraviti sedam ovakvih različitih uzoraka koji daju 7 bazičnih rešenja. Disk sa ovako ucrtanim trouglovima treba postaviti na nepokretni disk pomoću igle kroz centre oba diska. Postupak generisanja rešenja sastoji se u sledećem:
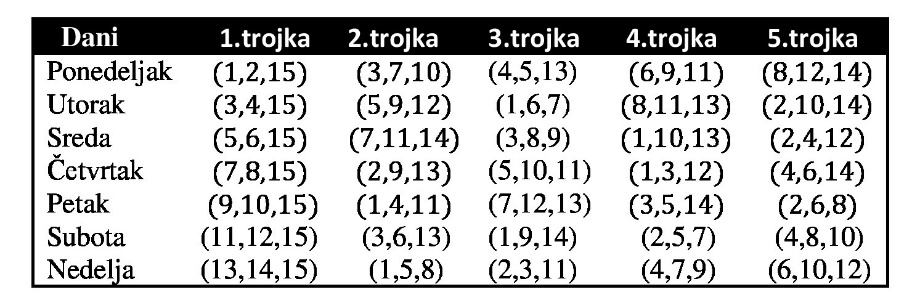
Početni položaj u kome se brojevi sa kružnica oba diska poklapaju daje raspored trojki za prvi dan: to je (1, 2, 15), (3, 7, 10), (4, 5, 13), (6, 9, 11), (8, 12, 14). Raspored za sledećih šest dana dobićemo rotacijom gornjeg diska za dve jedinice u proizvoljnom smeru. To znači da tačku na rotirajućem disku treba redom poklapati sa brojevima 3, 5, 7, 9, 11 i 13 na nepokretnom disku (ili u obratnom redosledu, što je svejedno). Temena trouglova na rotirajućem disku, zajedno sa centrom 15, nalaze se naspram brojeva na nepokretnom disku određujući na taj način tražene trojke. Kompletno rešenje (za uzorak sa slike 1) je dato u sledećoj tabeli:
Prema mišljenju velikog britanskog matematičara Džejmsa Silvestera (James Joseph Sylvester, 1814-1897), koji je takođe bio zainteresovan za ovaj problem, jedno od najinteresantnijih rešenja Kirkmanovog problema dao je B. Pirs (Pierce) u naučnom radu Cyclic solutions of the school-girl puzzle (The Astronomical Journal, vol. VI, 1859-1861). U svojoj knjizi Mathematical Recreations and Essays Rauz Bol i Kokseter dali su jedno rešenje za svako n (oblika 6m+3) manje od 100. Inače, Silvester se veoma interesovao za Štajnerove sisteme trojki i radio na ovoj temi dvadesetak godina, sve do svoje smrti. On je primetio da postoji (n nad 3) = 455 načina da se formiraju trojke od 15 učenica. Kako je 455=13 x 35, 35 = 7 dana x 5 trojki, sledi da je broj trojki koji bi eventualno mogao da formira Kirkmanove trojke jednak 13.
Međutim, koji skup od 35 Štajnerovih sistema trojki zadovoljava Kirkmanove uslove? U vezi s tim, Silvester je postavio sledeći problem: Da li se može aranžirati 455 različitih trojki u 13 različitih Štajnerovih sistema trojki koji bi zadovoljili uslove Kirkmanovog problema?
Silvesterov problem je vrlo težak i on nije dočekao da vidi rešenje (umro je 1897). Odgovor je nađen tek 1974. kada je R. Denison sa Lester univerziteta formulisao rešenje koristeći računar (Discrete Mathematics, No 9, 1974). Program na računaru radio je nešto više od 7 sati.
Drugi Silvesterov zadatak bio je, takođe, veoma težak: Da li je moguće aranžirati bilo koji konačan broj tačaka u ravni tako da prava kroz svaki skup od dve tačke može da prođe i kroz treću tačku, izuzimajući slučaj kada sve tačke leže na istoj pravoj?
Nažalost, Silvester nije video rešenje ni ovog svog problema. T. Grinvald (1944) je bio prvi koji je dao ispravno rešenje: odgovor je da traženi uzorak ne postoji.
U nastavku će biti izloženo nekoliko zadataka koji su zasnovani na Štajner-Kirkmanovim sistemima.
Dva Dudenijeva zadatka (Henri Dudeni bio je najveći engleski sastavljač logičkih matematičkih zadataka i zagonetki).
Zadatak 1. Dudeni je postavio pitanje konstrukcije uzorka u ravni sa 16 pravaca po 3 tačke u svakom. On je zadatak formulisao u vidu kratke priče iz Prvog svetskog rata čija (humana) adaptacija glasi ovako: Na bojnom polju 16 ruskih vojnika opkolilo je 11 turskih vojnika. Svaki ruski vojnik je pucao samo jednom i svaki metak je prošao kroz turbane tri turska vojnika. Koliko turskih vojnika ima neprobušene turbane?
Na osnovu slike 2 sledi odgovor: Nijedan. Pozicije ruskih vojnika se nalaze u produžetku svake duži, od kojih svaka sadrži po tri date tačke – turske vojnike.
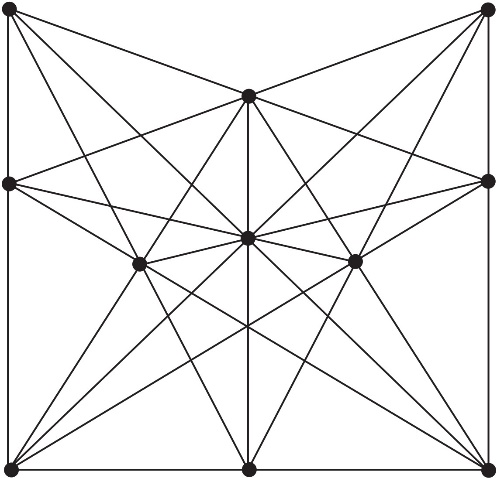
Sl. 2 11 tačaka na 16 pravih sa tačno 3 tačke na svakoj
Zadatak 2. U slučaju kada je k = 4 (Štajnerov sistem Sn(4), problem je znatno teži. Rešenje sa n = 16, 15 pravaca po k = 4 na svakom, Dudeni je prikazao na slici 3. Ovaj pentagonalni uzorak podseća na rascvetani cvet Hoya carnosa (sl. 4) iz familije Hoya koji raste u istočnoj Aziji i Australiji.
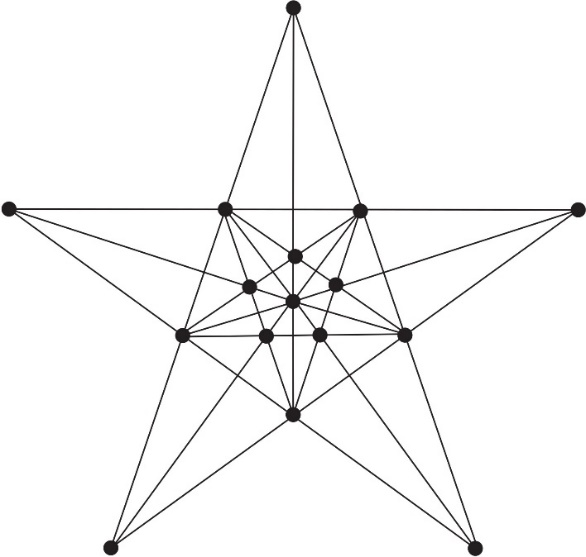

Sl. 3a 16 tačaka u 15 pravaca sa tačno 4 tačke na svakoj, 3b Uzorak cveta
Problem golf igrača. U rešenjima su korišćena slova abedede A-T u prvom zadatku i A-X u drugom zadatku.
Zadatak 3. 20 golfera želi da igra u četvorki 5 dana. Da li je moguće da svaki golfer ne igra više od jednom sa bilo kojim drugim golferom? Odgovor je da, a sledeća tabela daje rešenje (videti sajt https://mathworld.wolfram.com/SocialGolferProblem.html)
|
Dan 1 |
ABCD |
EFGH |
IJKL |
MNOP |
QRST |
|
Dan 2 |
AEIM |
BJOQ |
CHNT |
DGLS |
FKPR |
|
Dan 3 |
AGKO |
BIPT |
CFMS |
DHJR |
ELNQ |
|
Dan 4 |
AHLP |
BKNS |
CEOR |
DFIQ |
GJMT |
|
Dan 5 |
AFJN |
BLMR |
CGPQ |
DEKT |
HIOS |
Zadatak 4. 24 golf igrača mogu igrati u četvorki 7 dana, kao što se vidi iz rešenja sa sajta https://www.mathpuzzle.com/MAA/54-Golf%20Tournaments/mathgames_08_14_07.html).
Day1 ABKU IJSE QRCM DGFX HLNO PTVW
Day2 ACLV IKTF QSDN EHGR BMOP JUWX
Day3 ADMW ILUG QTEO FBHS CJNP KRVX
Day4 AENX IMVH QUFP GCBT DJKO LRSW
Day5 AFOR INWB QVGJ HDCU EKLP MSTX
Day6 AEPS IOXC QWHK BEDV FJLM NRTU
Day7 AHJT IPRD QXBL CFEW GKMN OSUV
Organizatori kuglanja, golfa, bridža ili tenisa često se bave problemima ove vrste, nemajući u vidu njihovu složenost. U opšem slučaju problem nema rešenja.