У овом прилогу аутор описује своја сазнања о обарању једног необичног рекорда баш на дан почетка НАТО бомбардовања марта 1999. Реч је о конструкцији шаховске партије где се захтева да се у најмањем броју потеза стигне до завршне реми позиције у којој противници остају само са краљевима. Проблем је поставио чувени композитор математичких загонетки и шаховских проблема Сем Лојд и сам креирао рекордно најкраћу партију у 17 потеза 1895. године. После читавог столећа рекорд је оборио италијански композитор ретроградних шаховских проблема Ђироламо Понцето смањујући дужину партије за један полупотез, што је била светска сензација.

Проф. др Миодраг Петковић
Американац Семјуел Лојд (1841-1911, Филаделфија, или Сем, име које се најчешће помиње у литератури), по мишљењу многих аутора је највећи састављач математичких и логичких загонетки али и шаховских проблема свих времена. Један од најинтересантнијих проблема из његове збирке је, свакако, конструкција шаховске партије из 1895. године где оба играча у регуларној партији врше „масакр” свих противничних шаховских фигура и најзад остају само с краљевима на табли. Партије овог типа су познате под именом 2-краља (2-kings). Лојд је дао решење у 17 потеза, тј. играчи са белим и црним фигурама играју по 17 полупотеза свако (укупно 34 полупотеза). По строгим шаховски правилима ово не би могао да се прихвати као регуларан шаховски проблем јер решење није јединствено. Међутим, Лојдов задатак је довољно изазован, интересантан, а и врло тежак да испуњење наведеног услова није ни битно за решаваче.
Нагласимо да не треба бити шаховски професионалац да би се укључио у решавање овог проблема, довољно је познавање основних шаховских правила. Током ових сто година, нарочито у последње три деценије, за решавање су коришћени и рачунари. Током овог дугог временског периода увек се логично постављало и следеће питање: Да ли се до „голих” краљева може стићи и брже, тј. у мање од 17 потеза?
Стицајем повољних околности био сам један од првих који је сазнао за обарање Лојдовог рекорда. Наиме, крајем деведестих година прошлог века имао сам интензивну имејл корспонденцију са Мариом Велучијем, професором компјутерских наука на Универзитету у Пизи (Италија). Преписка је започела дискусијама поводом моје тек објављене књиге Mathematics and Chess (Dover Publications, New York 1997) и перспективе рачунара у шаху, што је била актуелна тема у то време после победе ИБМ-овог шаховског компјутера Deep Blue над светским прваком Гаријем Kаспаровим 1997. године. Осим тога, обојица смо се бавили компоновањем шаховских проблема при чему је Велучи уживао далеко већи реноме бавећи са ретроградним шаховским проблемима. Поменимо да је ретроградна анализа нека врста шаховског времеплова где се разматрају реконструкције (шаховске) игре, докази легалности тренутне позиције или шаховске партије у целини, затим питања као што су ко је на потезу, да ли је могућ мат у X потеза, да ли једна страна може да изврши рокаду и слично. Управо је ретроградна анализа помогла рушењу Лојдовог рекорда.
Да бисмо читаоцима који се не баве шаховским проблемима али познају правила шаховске игре дочарали лепоту ретроградних проблема, на дијаграму смо приказали једноставан пример: једине фигуре на табли су бели краљ на h5 и црни краљ на е8. Бели и црни враћају по један потез, затим црни игра други потез којим помаже белом да га матира својим следећим потезом.
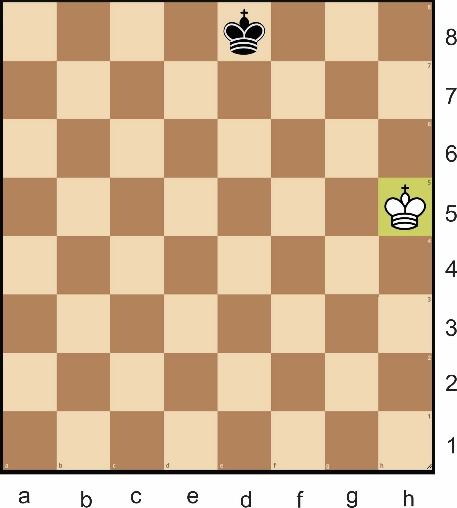
Решење је једноставно и несумњиво маштовито. Уместо да потезом Kg6:h5 бели узме црног топа на h5, он враћа краља на g6, затим црни враћа свог топа са поља h5, на коме је узео белу даму (!), на поље h8, врши малу рокаду (!), после чега бели даје мат са Dh5-h7.
Вратимо се партијама „2-краља”: 24. марта 1999. године добио сам Велучијев имејл у коме ме је информисао да је италијански проблемист Ђироламо Понцето, користећи делом и ретроградну анализу, конструисао најкраћу могућу партију од 16 и по потеза, тј. од 33 полупотеза, за пола потеза мање од Лојдове партије, у којој противници остају само са краљевима. Марио Велучи био је консултат по питању рачунарских програма. Понцето је публиковао овај рекорд у часопису T&C-Scacco! у јануару 2000. године. Велучи ми је у имејлу у шаховској нотацији послао све потезе ове партије. Веома интригaнтно, имејл се завршавао злокобним информацијом у облику врло једноставног питања: Afraid?
Kао и већина Италијана (такође и држављана земаља чланова НАТО алијансе), Велучи је знао да ће из НАТО база и са носача авиона полетети авиони и навођене ракете са циљем да бомбардују Србију. Заиста, тог дана су пале прве НАТО бомбе и крстареће ракете типа томахавк на градове у Србији тако да је датум Велучијевог имејла било лако упамтити за сва времена. Велучијев имејл би могао да се схвати као порука која носи једну добру и једну лошу вест, при чему је од оне прве мала практична корист, а друга је наговестила хуману катастрофу и огромна материјална разарања.
После објављивања Понцетовог решење у 16,5 потеза у јануару 2000, Марио Велучи је у априлу 2000. послао циркуларни имејл великом броју заљубљеника у шаховске проблеме и компјутерски шах тако да је Понцетово решење постало познато широм света. У Србију је решење дошло годину дана раније, нажалост, заједно са бомбама. Аутор овог прилога је креирао видео-приказ ове партије који се може видети на линку
https://www.youtube.com/results?search_query=fastest+chess+game+massacre под називом Fastest chess massacre game.
Понцетијева рекордна 33-полупотезна партија „2-краља” приказана је такође помоћу 33 шаховских дијаграма, при чему сваки дијаграм приказује један полупотез партије. Аутор је мишљења да се на овај олакшава праћење партије оним читаоцима који нису вични шаховској нотацији или немају интернет.



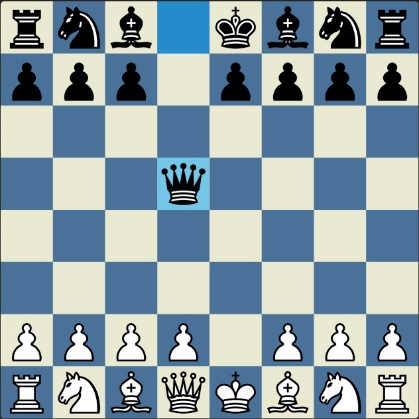

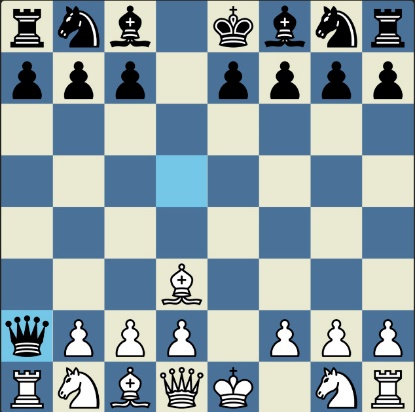


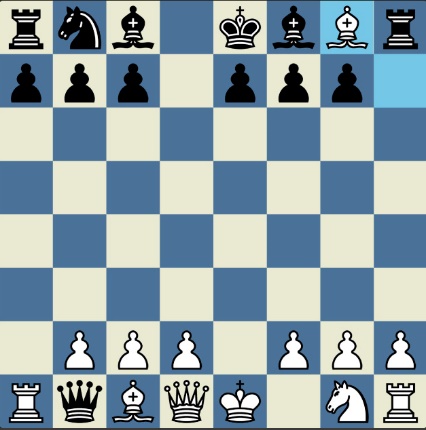
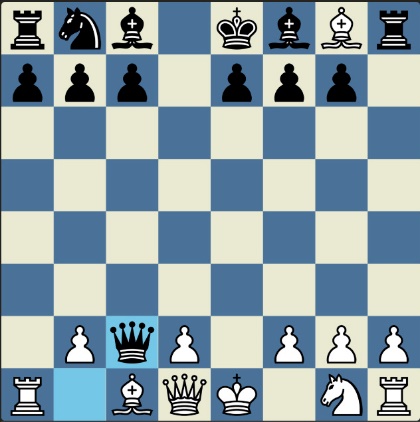
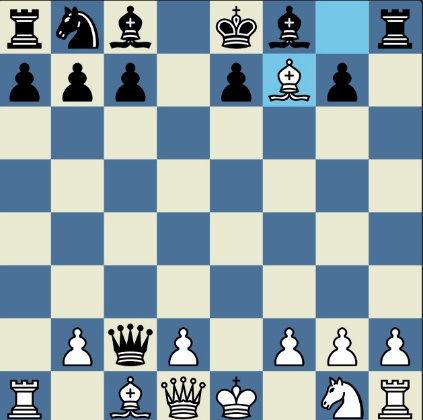
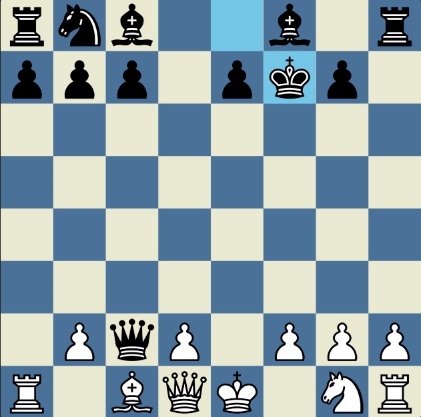
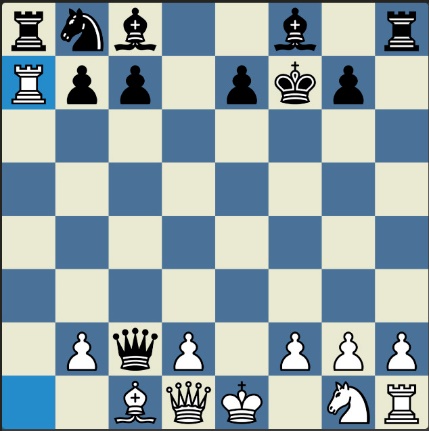
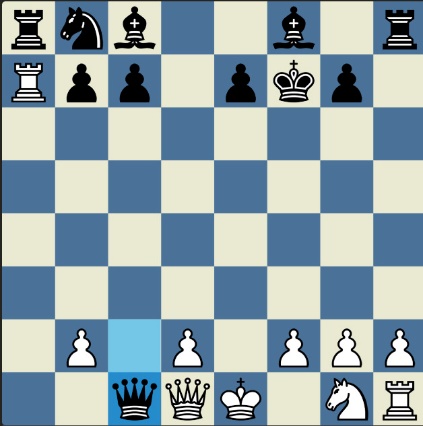
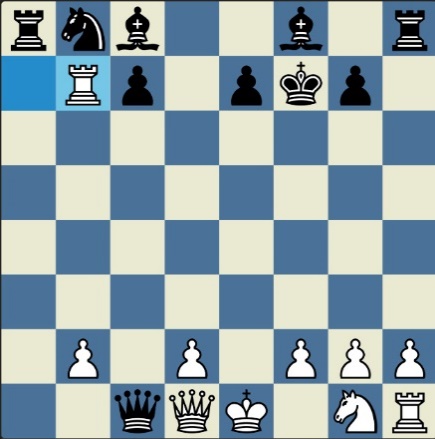
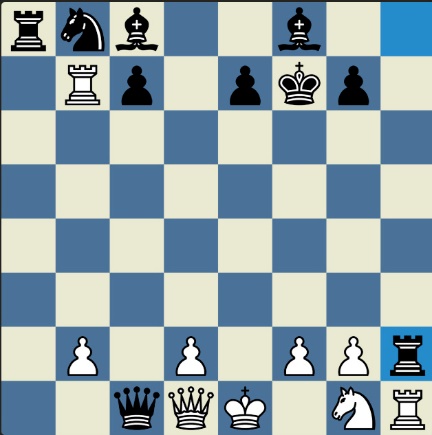
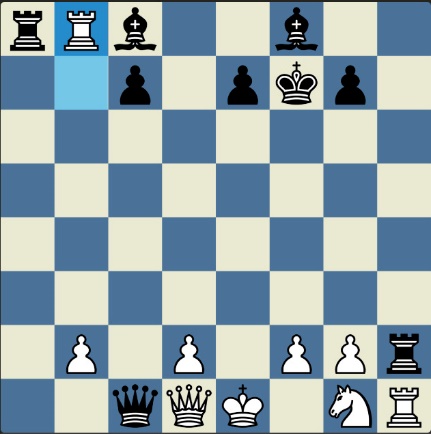
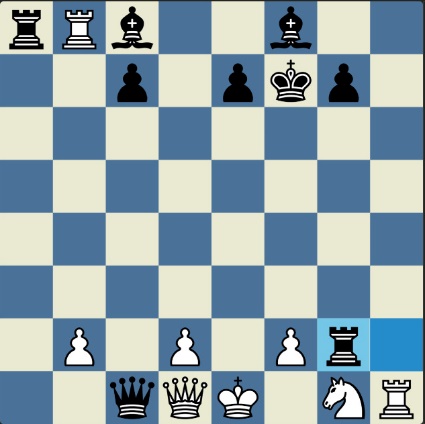
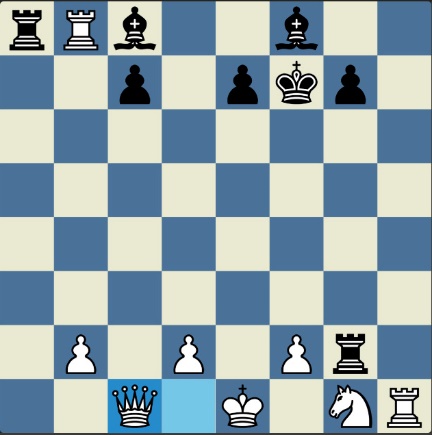
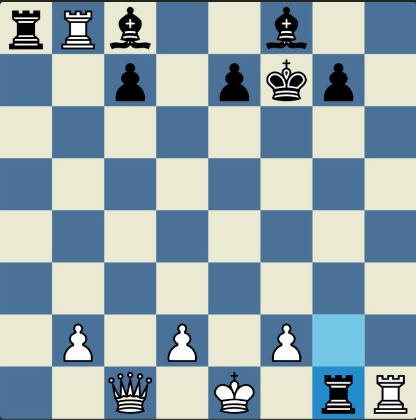
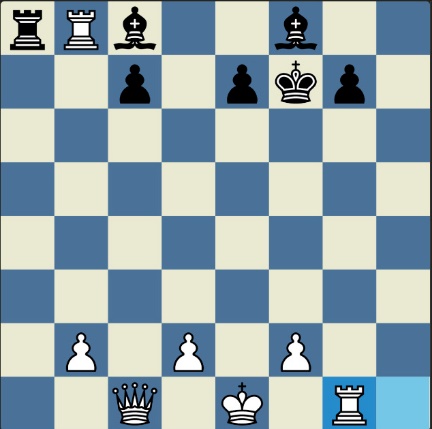
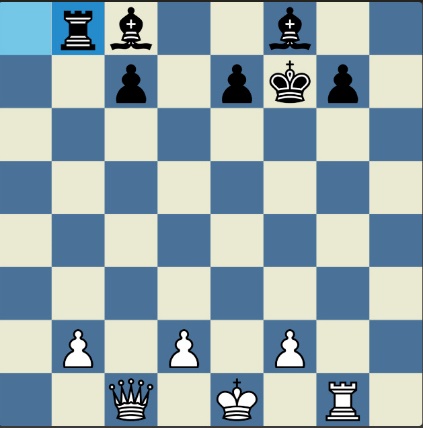
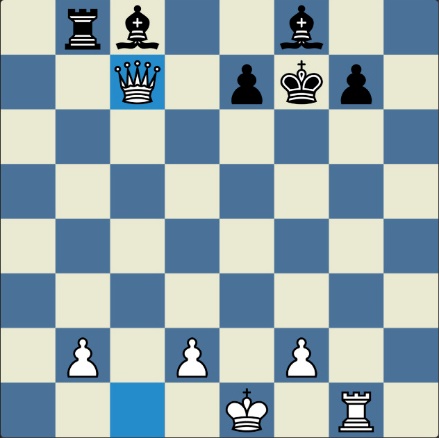
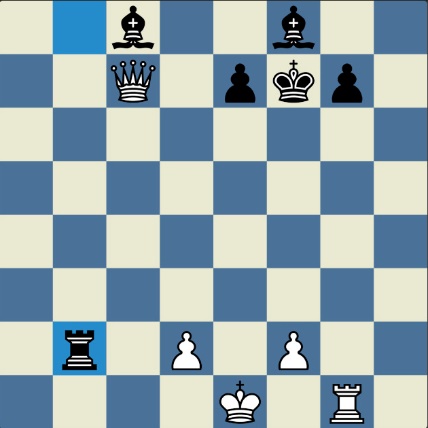
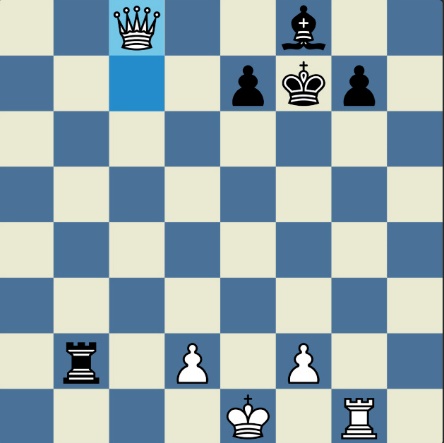
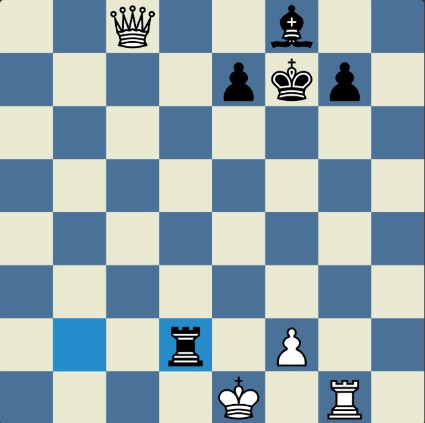
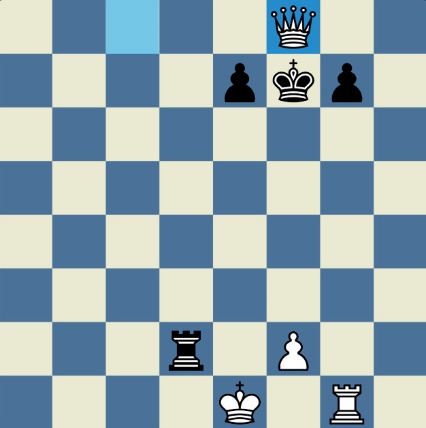
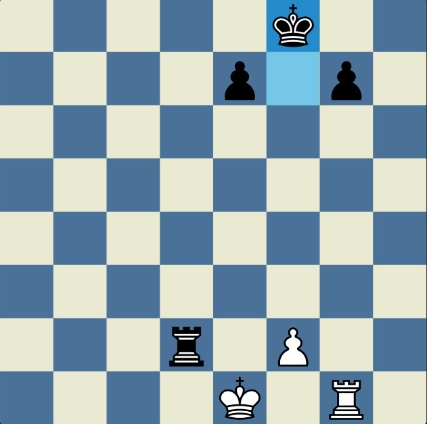
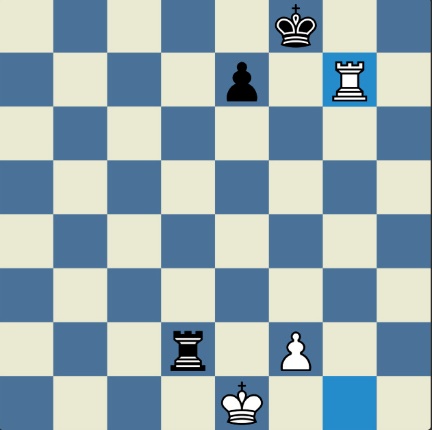
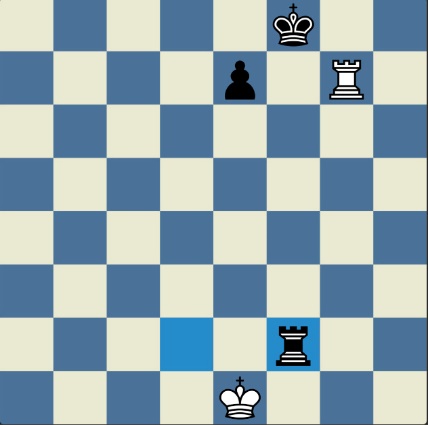
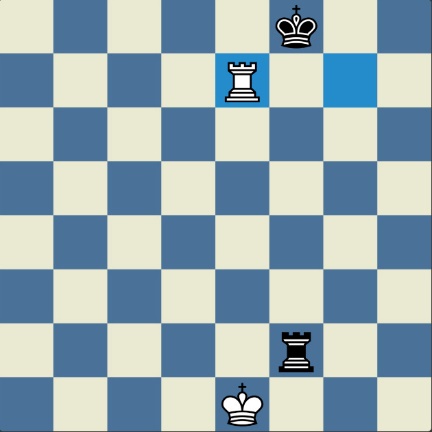


„У ноћи док је Kристијан летео за Тунис (није релевантно за причу мада је те ноћи Kристијан стварно летео за Тунис)” [др Боби], шта се даље десило? После објављивања Понцетијеве најкраће партије „2-краља”, програмери и љубитељи шаховских проблема жестоким темпом су кренули у трагање за другим решењима али и за доказима да је 33 полупотеза минималан број у партији 2-краља. Очигледно је да је: 1) за узимање 15 белих и 15 црних фигура потребно 30 полупотеза, 2) у прва два полупотеза није могуће узимање противничких фигура, 3) постоји бар један „мртав” потез у наставку партије када нема узимања. и то је 33. Доказ се заснива на чињеници да постоји бар један „мртав” потез и то је установљено brute-force претраживањем помоћу супербрзих рачунара. У Понцетијевој партији то је потез белог 2. Ld3. Према томе, до „голих” краљева (шаховски сленг) се не може стићи у мање од 33 полупотеза (16 и по потеза, како неки аутори више воле да кажу).
Kакав је био резултат ове потраге за другим решењима (кад је Kристијан вероватно већ слетео у Тунис)? [др Боби] Према ауторовом сазнању, досад је конструисано осам „2-краља” партија од 16,5 потеза, али са додатно уведеним релаксационим „правилом” да – ако је краљ нападнут он може играти као било фигура, што није по шаховским правилима. За краља са овом додатном особином смишљен је и термин Vaulting King, што би у слободном преводу означавало да нападнути краљ (краљ под шахом) може да скаче/игра са ослонцем, тј. као произвољна шаховска фигура. (У атлетици се за дисциплину скок с мотком користи енглеска фраза pole vault). Партије овог типа се врло ретко узимају у обзир тако да Понцетова партија „2-краља” у 16,5 потеза је засад најкраћа по ауторовом сазнању. Аутор би био врло захвалан читаоцима који би овај прилог употпунили новим информацијама о некој другој партији до „голих” краљева у 16,5 потеза.
У овом прилогу писао сам о шаху и рачунарима. Kореспонденција са професором Мариом Велучијем довела ме је до информације о рекорду који је постигао Понцето – шаховске партије у којој на крају остају само краљеви. Чудном коинциденцијом, на дан НАТО напада на Србију. Поменуо сам и шаховски рачунар Deep Blue и ризикујући да одем у дигресију, поменућу још једну коинциденцију држећи се тематике овог прилога.
За време боравка на Универзитету Харвард у септембру 2009. године мени и мојој супрузи професорки Љиљани Петковић домаћин је био математичар (computational complexity theory) и светски експерт на пољу рачунарских наука Хсианг-Т. Kунг, рођен на Тајвану. Професор Kунг је био светски познат и признат због идеје о компјутерској паралелизацији и њеној надградњи, систоличким пољима, области која је касније послужила као основа за неуронске мреже и вештачку интелигенцију. Није без интереса рећи да се систоличким пољима успешно бавио професор Миле Стојчев са Електронског факултету у Нишу са својим тимом. Разуме се да сам део њихових резултата доставио професору Kингу, поносан што се и на једном српском факултету изучава тако важна област.
Управо у време нашег боравка појавила се из штампе моја књига Famous Puzzles of Great Mathematicians у издању Америчког математичког друштва (AMS). Док смо разговарали о перспективама компјутерског шаха (с незаобилазном темом о поменутом ИБМ рачунару Deep Blue), ја сам поклонио примерак ове књиге професору Kунгу. Он се захвалио, а затим је брзо устао и из суседне просторије донео књигу Behind Deep Blue, аутора Фенг-Хсиунг Хсуа, такође Тајванца. „Аутор ове књиге је Фенг Хсу, он је направио Deep Blue који је победио светског првака у шаху. Хсу је годинама био опседнут дизајнирањем специјализованог компјутерског чипа. „Једва сам га наговорио да преда докторску дисетацију”, рекао је Kунг поклањајући ми ову књигу с посветом. За мене је то био веома вредан поклон јер сам могао из прве руке да испратим читаву историју дизајнирања и конструкције рачунара Deep Blue који је победио Гарија Kаспарова 1997.

Професори Љиљана и Миодраг Петковић
са професором Х.Т Kунгом (Харвард, 2009)

Насловна страна Хсуове књиге
(Илустрација Миодраг Петковић)








