U ovom prilogu autor opisuje svoja saznanja o obaranju jednog neobičnog rekorda baš na dan početka NATO bombardovanja marta 1999. Reč je o konstrukciji šahovske partije gde se zahteva da se u najmanjem broju poteza stigne do završne remi pozicije u kojoj protivnici ostaju samo sa kraljevima. Problem je postavio čuveni kompozitor matematičkih zagonetki i šahovskih problema Sem Lojd i sam kreirao rekordno najkraću partiju u 17 poteza 1895. godine. Posle čitavog stoleća rekord je oborio italijanski kompozitor retrogradnih šahovskih problema Đirolamo Ponceto smanjujući dužinu partije za jedan polupotez, što je bila svetska senzacija.

Prof. dr Miodrag Petković
Amerikanac Semjuel Lojd (1841-1911, Filadelfija, ili Sem, ime koje se najčešće pominje u literaturi), po mišljenju mnogih autora je najveći sastavljač matematičkih i logičkih zagonetki ali i šahovskih problema svih vremena. Jedan od najinteresantnijih problema iz njegove zbirke je, svakako, konstrukcija šahovske partije iz 1895. godine gde oba igrača u regularnoj partiji vrše „masakr” svih protivničnih šahovskih figura i najzad ostaju samo s kraljevima na tabli. Partije ovog tipa su poznate pod imenom 2-kralja (2-kings). Lojd je dao rešenje u 17 poteza, tj. igrači sa belim i crnim figurama igraju po 17 polupoteza svako (ukupno 34 polupoteza). Po strogim šahovski pravilima ovo ne bi mogao da se prihvati kao regularan šahovski problem jer rešenje nije jedinstveno. Međutim, Lojdov zadatak je dovoljno izazovan, interesantan, a i vrlo težak da ispunjenje navedenog uslova nije ni bitno za rešavače.
Naglasimo da ne treba biti šahovski profesionalac da bi se uključio u rešavanje ovog problema, dovoljno je poznavanje osnovnih šahovskih pravila. Tokom ovih sto godina, naročito u poslednje tri decenije, za rešavanje su korišćeni i računari. Tokom ovog dugog vremenskog perioda uvek se logično postavljalo i sledeće pitanje: Da li se do „golih” kraljeva može stići i brže, tj. u manje od 17 poteza?
Sticajem povoljnih okolnosti bio sam jedan od prvih koji je saznao za obaranje Lojdovog rekorda. Naime, krajem devedestih godina prošlog veka imao sam intenzivnu imejl korspondenciju sa Mariom Velučijem, profesorom kompjuterskih nauka na Univerzitetu u Pizi (Italija). Prepiska je započela diskusijama povodom moje tek objavljene knjige Mathematics and Chess (Dover Publications, New York 1997) i perspektive računara u šahu, što je bila aktuelna tema u to vreme posle pobede IBM-ovog šahovskog kompjutera Deep Blue nad svetskim prvakom Garijem Kasparovim 1997. godine. Osim toga, obojica smo se bavili komponovanjem šahovskih problema pri čemu je Veluči uživao daleko veći renome baveći sa retrogradnim šahovskim problemima. Pomenimo da je retrogradna analiza neka vrsta šahovskog vremeplova gde se razmatraju rekonstrukcije (šahovske) igre, dokazi legalnosti trenutne pozicije ili šahovske partije u celini, zatim pitanja kao što su ko je na potezu, da li je moguć mat u X poteza, da li jedna strana može da izvrši rokadu i slično. Upravo je retrogradna analiza pomogla rušenju Lojdovog rekorda.
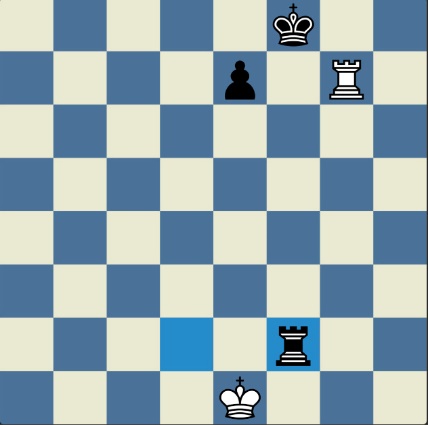
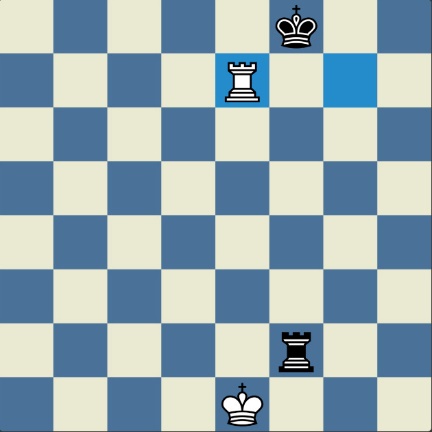
Da bismo čitaocima koji se ne bave šahovskim problemima ali poznaju pravila šahovske igre dočarali lepotu retrogradnih problema, na dijagramu smo prikazali jednostavan primer: jedine figure na tabli su beli kralj na h5 i crni kralj na e8. Beli i crni vraćaju po jedan potez, zatim crni igra drugi potez kojim pomaže belom da ga matira svojim sledećim potezom.
Rešenje je jednostavno i nesumnjivo maštovito. Umesto da potezom Kg6:h5 beli uzme crnog topa na h5, on vraća kralja na g6, zatim crni vraća svog topa sa polja h5, na kome je uzeo belu damu (!), na polje h8, vrši malu rokadu (!), posle čega beli daje mat sa Dh5-h7.
Vratimo se partijama „2-kralja”: 24. marta 1999. godine dobio sam Velučijev imejl u kome me je informisao da je italijanski problemist Đirolamo Ponceto, koristeći delom i retrogradnu analizu, konstruisao najkraću moguću partiju od 16 i po poteza, tj. od 33 polupoteza, za pola poteza manje od Lojdove partije, u kojoj protivnici ostaju samo sa kraljevima. Mario Veluči bio je konsultat po pitanju računarskih programa. Ponceto je publikovao ovaj rekord u časopisu T&C-Scacco! u januaru 2000. godine. Veluči mi je u imejlu u šahovskoj notaciji poslao sve poteze ove partije. Veoma intrigantno, imejl se završavao zlokobnim informacijom u obliku vrlo jednostavnog pitanja: Afraid?
Kao i većina Italijana (takođe i državljana zemalja članova NATO alijanse), Veluči je znao da će iz NATO baza i sa nosača aviona poleteti avioni i navođene rakete sa ciljem da bombarduju Srbiju. Zaista, tog dana su pale prve NATO bombe i krstareće rakete tipa tomahavk na gradove u Srbiji tako da je datum Velučijevog imejla bilo lako upamtiti za sva vremena. Velučijev imejl bi mogao da se shvati kao poruka koja nosi jednu dobru i jednu lošu vest, pri čemu je od one prve mala praktična korist, a druga je nagovestila humanu katastrofu i ogromna materijalna razaranja.
Posle objavljivanja Poncetovog rešenje u 16,5 poteza u januaru 2000, Mario Veluči je u aprilu 2000. poslao cirkularni imejl velikom broju zaljubljenika u šahovske probleme i kompjuterski šah tako da je Poncetovo rešenje postalo poznato širom sveta. U Srbiju je rešenje došlo godinu dana ranije, nažalost, zajedno sa bombama. Autor ovog priloga je kreirao video-prikaz ove partije koji se može videti na linku
https://www.youtube.com/results?search_query=fastest+chess+game+massacre pod nazivom Fastest chess massacre game.
Poncetijeva rekordna 33-polupotezna partija „2-kralja” prikazana je takođe pomoću 33 šahovskih dijagrama, pri čemu svaki dijagram prikazuje jedan polupotez partije. Autor je mišljenja da se na ovaj olakšava praćenje partije onim čitaocima koji nisu vični šahovskoj notaciji ili nemaju internet.



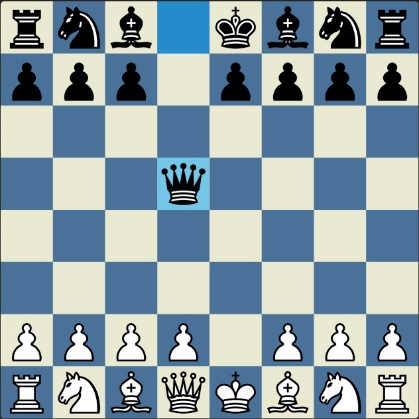

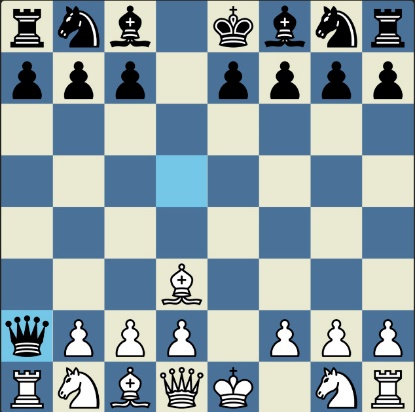


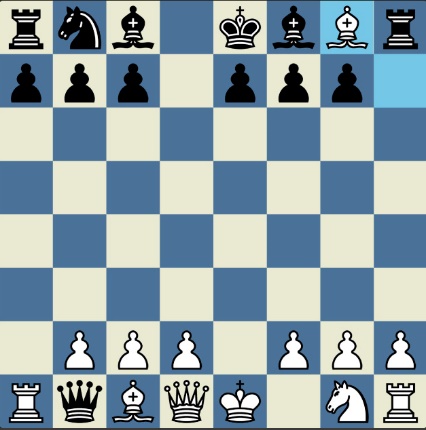
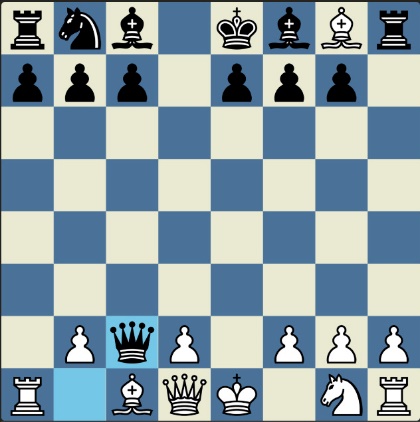
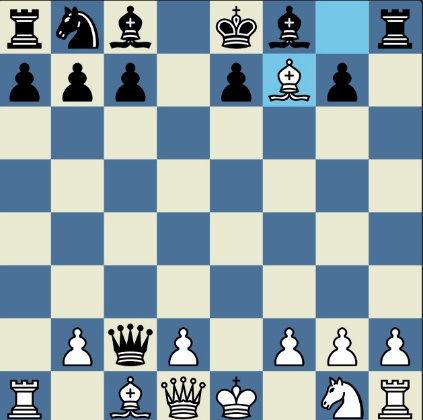
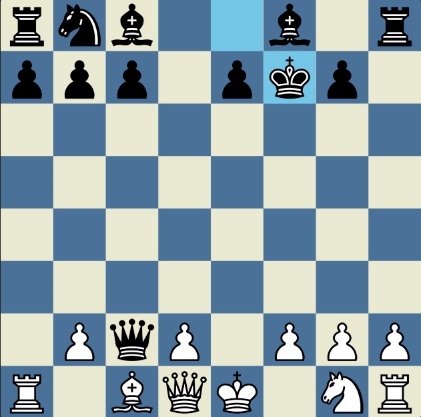
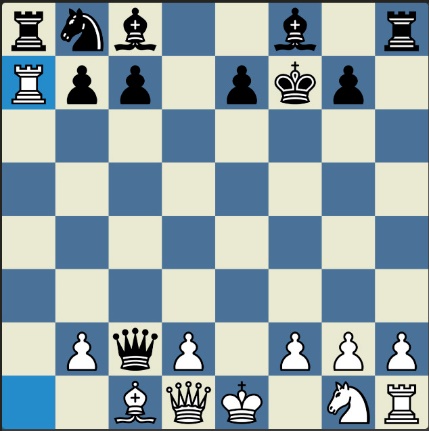
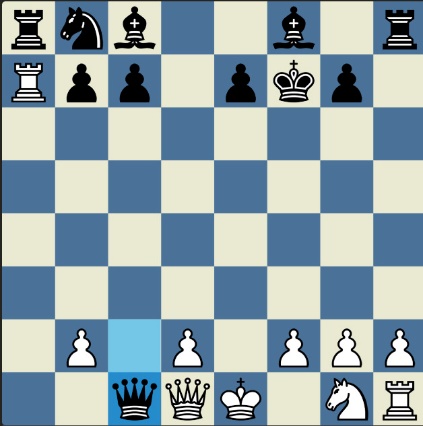
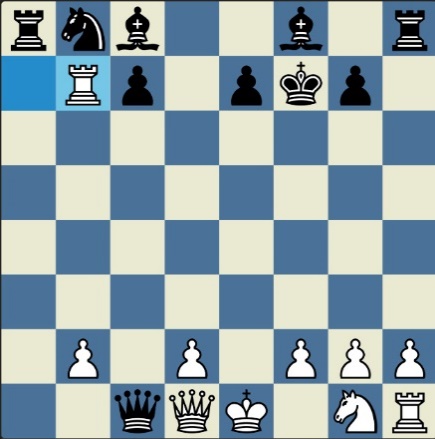
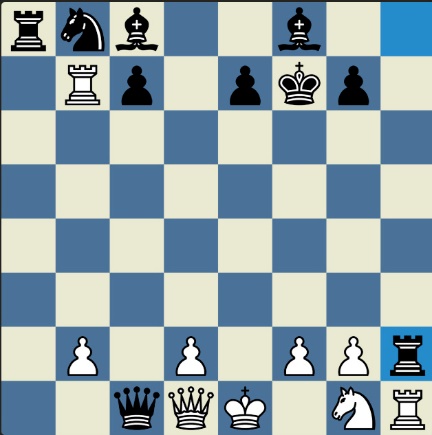
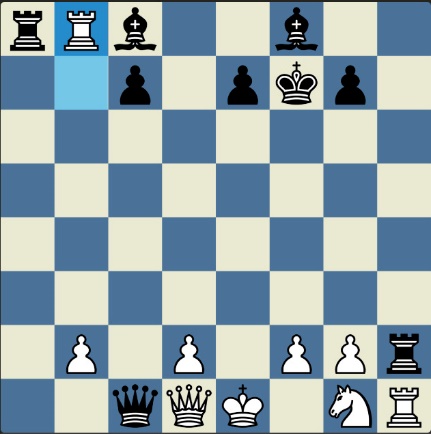
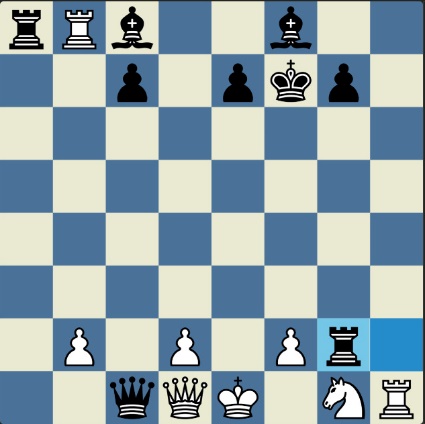
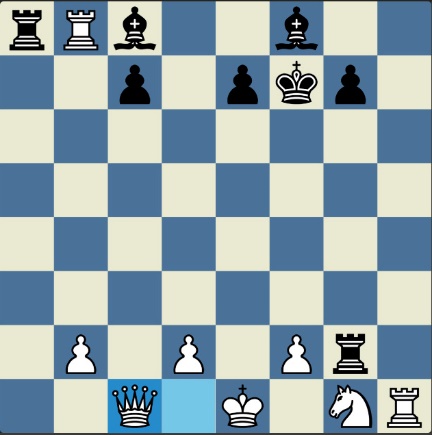
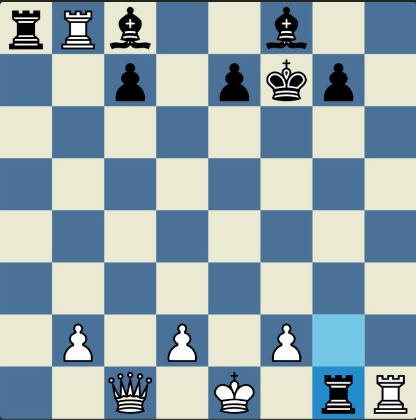
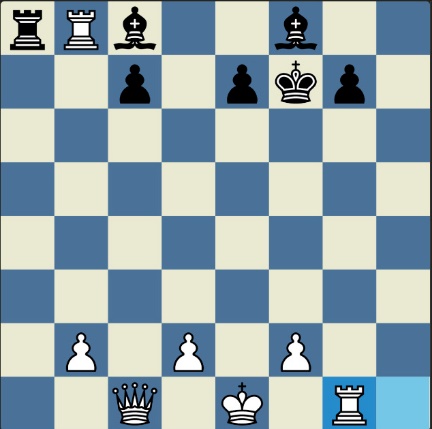
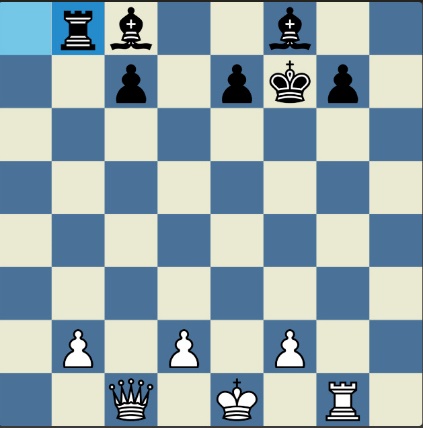
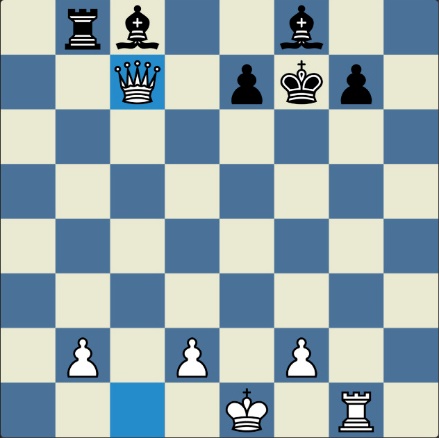
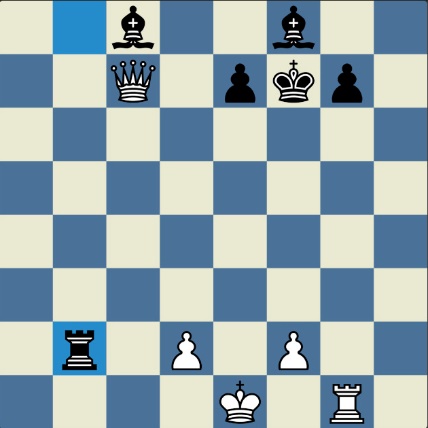
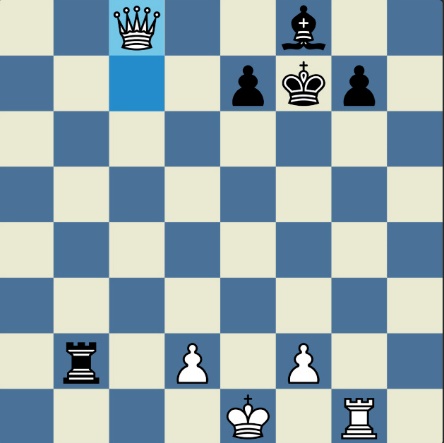
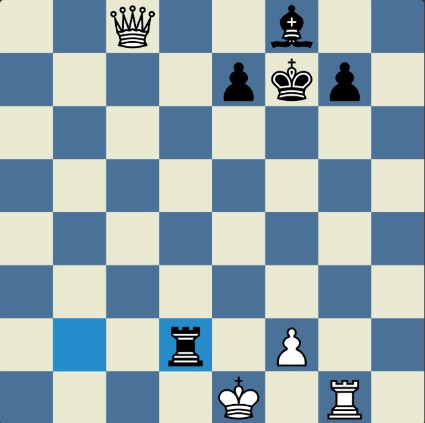
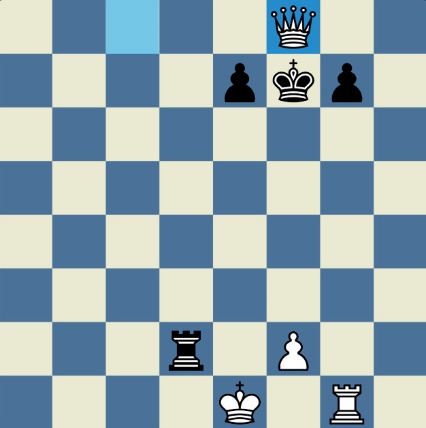
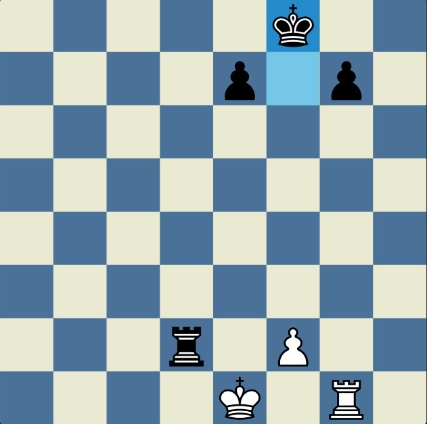
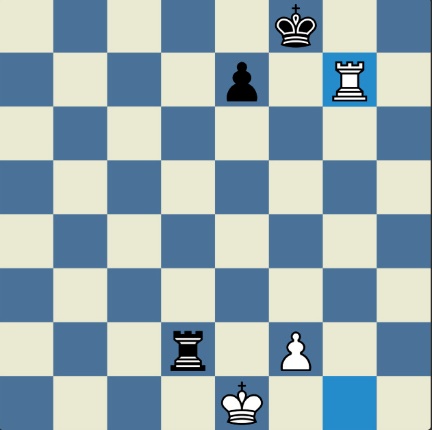


„U noći dok je Kristijan leteo za Tunis (nije relevantno za priču mada je te noći Kristijan stvarno leteo za Tunis)” [dr Bobi], šta se dalje desilo? Posle objavljivanja Poncetijeve najkraće partije „2-kralja”, programeri i ljubitelji šahovskih problema žestokim tempom su krenuli u traganje za drugim rešenjima ali i za dokazima da je 33 polupoteza minimalan broj u partiji 2-kralja. Očigledno je da je: 1) za uzimanje 15 belih i 15 crnih figura potrebno 30 polupoteza, 2) u prva dva polupoteza nije moguće uzimanje protivničkih figura, 3) postoji bar jedan „mrtav” potez u nastavku partije kada nema uzimanja. i to je 33. Dokaz se zasniva na činjenici da postoji bar jedan „mrtav” potez i to je ustanovljeno brute-force pretraživanjem pomoću superbrzih računara. U Poncetijevoj partiji to je potez belog 2. Ld3. Prema tome, do „golih” kraljeva (šahovski sleng) se ne može stići u manje od 33 polupoteza (16 i po poteza, kako neki autori više vole da kažu).
Kakav je bio rezultat ove potrage za drugim rešenjima (kad je Kristijan verovatno već sleteo u Tunis)? [dr Bobi] Prema autorovom saznanju, dosad je konstruisano osam „2-kralja” partija od 16,5 poteza, ali sa dodatno uvedenim relaksacionim „pravilom” da – ako je kralj napadnut on može igrati kao bilo figura, što nije po šahovskim pravilima. Za kralja sa ovom dodatnom osobinom smišljen je i termin Vaulting King, što bi u slobodnom prevodu označavalo da napadnuti kralj (kralj pod šahom) može da skače/igra sa osloncem, tj. kao proizvoljna šahovska figura. (U atletici se za disciplinu skok s motkom koristi engleska fraza pole vault). Partije ovog tipa se vrlo retko uzimaju u obzir tako da Poncetova partija „2-kralja” u 16,5 poteza je zasad najkraća po autorovom saznanju. Autor bi bio vrlo zahvalan čitaocima koji bi ovaj prilog upotpunili novim informacijama o nekoj drugoj partiji do „golih” kraljeva u 16,5 poteza.
U ovom prilogu pisao sam o šahu i računarima. Korespondencija sa profesorom Mariom Velučijem dovela me je do informacije o rekordu koji je postigao Ponceto – šahovske partije u kojoj na kraju ostaju samo kraljevi. Čudnom koincidencijom, na dan NATO napada na Srbiju. Pomenuo sam i šahovski računar Deep Blue i rizikujući da odem u digresiju, pomenuću još jednu koincidenciju držeći se tematike ovog priloga.
Za vreme boravka na Univerzitetu Harvard u septembru 2009. godine meni i mojoj supruzi profesorki Ljiljani Petković domaćin je bio matematičar (computational complexity theory) i svetski ekspert na polju računarskih nauka Hsiang-T. Kung, rođen na Tajvanu. Profesor Kung je bio svetski poznat i priznat zbog ideje o kompjuterskoj paralelizaciji i njenoj nadgradnji, sistoličkim poljima, oblasti koja je kasnije poslužila kao osnova za neuronske mreže i veštačku inteligenciju. Nije bez interesa reći da se sistoličkim poljima uspešno bavio profesor Mile Stojčev sa Elektronskog fakultetu u Nišu sa svojim timom. Razume se da sam deo njihovih rezultata dostavio profesoru Kingu, ponosan što se i na jednom srpskom fakultetu izučava tako važna oblast.
Upravo u vreme našeg boravka pojavila se iz štampe moja knjiga Famous Puzzles of Great Mathematicians u izdanju Američkog matematičkog društva (AMS). Dok smo razgovarali o perspektivama kompjuterskog šaha (s nezaobilaznom temom o pomenutom IBM računaru Deep Blue), ja sam poklonio primerak ove knjige profesoru Kungu. On se zahvalio, a zatim je brzo ustao i iz susedne prostorije doneo knjigu Behind Deep Blue, autora Feng-Hsiung Hsua, takođe Tajvanca. „Autor ove knjige je Feng Hsu, on je napravio Deep Blue koji je pobedio svetskog prvaka u šahu. Hsu je godinama bio opsednut dizajniranjem specijalizovanog kompjuterskog čipa. „Jedva sam ga nagovorio da preda doktorsku disetaciju”, rekao je Kung poklanjajući mi ovu knjigu s posvetom. Za mene je to bio veoma vredan poklon jer sam mogao iz prve ruke da ispratim čitavu istoriju dizajniranja i konstrukcije računara Deep Blue koji je pobedio Garija Kasparova 1997.

Profesori Ljiljana i Miodrag Petković
sa profesorom H.T Kungom (Harvard, 2009)

Naslovna strana Hsuove knjige
(Ilustracija Miodrag Petković)








