У историји математике посебно интересантно место заузимају проблеми из свакодневног живота који су привукли пазњу великих математичара. Решавајући их, они су дошли до резултата који су представљали зачетке нових математичких дисциплина. У овом прилогу биће изложена прича коју су покренули знатижељни становници Kенигсберга пре 250 година у вези с преласком преко свих мостова на реци која протиче кроз овај град. Проблем је решио један од највећих математичара свих времена, Леонард Ојлер, и то се сматра почетком теорије графова.

Проф. др Миодраг Петковић
Преко реке Прегел што протиче кроз град Kенигсберг (некада у Пруској, данас под именом Kалињинград у Русији), коју два острва деле на два рукавца, седам мостова повезују острва и обале реке. Становници су дуго су били заокупљени следећим питањем: Да ли је могуће прећи све мостове не прелазећи ни преко једног два или више пута? Упркос напорима, ниједан од знатижељника није остварио такву шетњу, нити је показао да је то изводљиво.
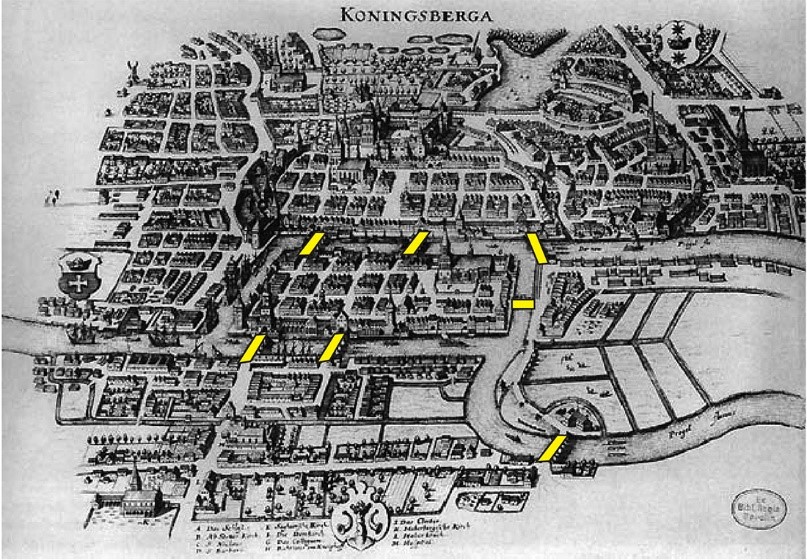
Сл. 1 Стари Kенигсберг и његових седам мостова (скица из 1651)
Проблем је решио чувени швајцарски математичар Леонард Ојлер (Leonhard Euler, 1707-1783) године 1736. Тај доказ непостојања жељеног пута обично се узима као почетак нове математичке дисциплине – теорије графова. Данас је она веома корисна не само у разним математичким гранама, већ и у другим научним дисциплинама као што су компјутерске и техничке науке, хемија, биологија, операциона истраживања, транспорт и логистика, друштвене науке итд.
Пре него што прикажемо решење, вреди рећи неколико речи о Леонарду Ојлеру кога с Њутном, Гаусом и Архимедом сврставају у највеће математичаре свих времена. Према обиму објављених радова, он је најпродуктивнији. Библиографска листа, укључујући и посмртно објављене радове, садрзи 886 јединица што би могло да испуни 80 књига великог формата или око 80.000 страница. У својој 59. Години он је остао скоро слеп након неке болести. Захваљујући невероватној меморији, последњих 17 година живота могао је да настави са радом у оптици, алгебри и проучавању лунарног кретања написавши скоро половину свих својих радова. Бавио се малтене свим областима математике, а повремено и проблемима рекреативне математике. Неки од тих излета довели су до настанка нових метода, чак и нових грана математике, као што је, на пример, теорија графова и топологија.
За оне који нису слушали курсеве из теорије графова дајемо преглед најосновнијих појмова, јер се тако решење може лако пратити. У теорији графова планарни граф се дефинише као скуп тачака у равни од којих су неке повезане линијама. Тачке се зову чворови или темена графа (нпр. тачке А, B, C, D, Е на слици 2а), а линије се назицају гране, спојнице или ивице. За грану која повезује два суседна чвора каже се да је инцидентна за оба. А за граф који нема петље (линије што полазе и завршавају у истом чвору, нпр. p на слици 2b) и немају две или више вишеструких грана које повезују исти пар чворова, каже се да је прост граф (слика 2а), у противном је мултиграф (слика 2b).
Степен чвора је број грана које су с њим инцидентне, рачунајући петље и вишеструке гране. Тако се степен чвора Т означава са deg(T). На пример, степени чворова на слици 2а су deg(A) = 2, deg(B) = 4, deg(C) = 2, deg(D) = 3, deg(E) = 1. Чвор графа који има непаран (паран) степен зове се непаран (паран) чвор.
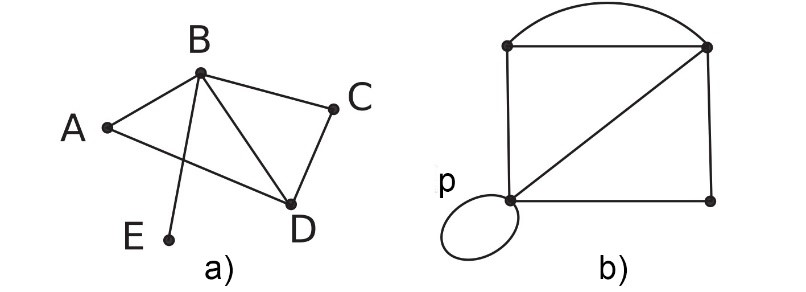
Сл. 2 Различити типови графова:
а) прост граф b) мулриграф
Вратимо се проблему кенигсбершких мостова и напоменимо да је он еквивалентан следећем проблему (видети слику 4, ради илустрације): Мрежа (граф) у равни добијена је спајањем датог скупа тачака помоћу линија. Под којим условима се ова мрежа може нацртати у једном потезу (не подижући оловку са папира) и не прелазећи по већ повученим линијама? Цртање графа у једном потезу обично се зове трасирање графа.
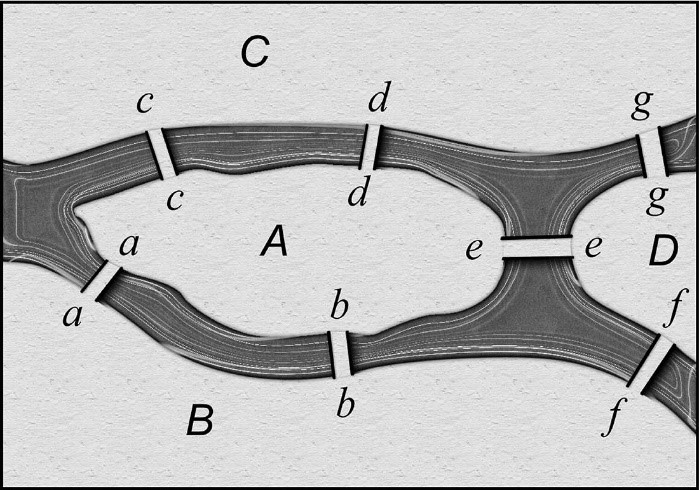
Сл. 3 Kенигсбершки мостови
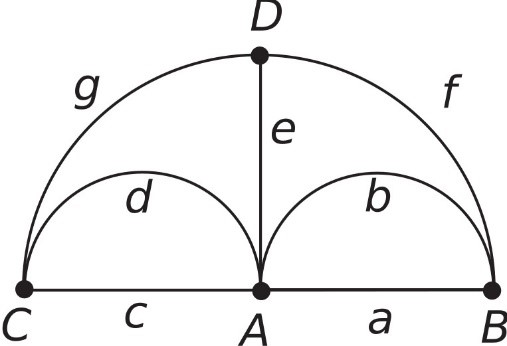
Сл. 4 Граф кенигсбершких мостова
Решење проблема кенигсбершких мостова и цртање раванске мреже (графа) у „једном потезу” (тј. без подизања оловке са папира) засновано је на следећем тврђењу: Ојлерова теорема: Граф се може трасирати без подизања оловке, прелазећи преко сваке ивице тачно једанпут, ако и само ако граф има два или ниједан чвор непарног степена.
Граф који се може трасирари под наведеним условима зове се Ојлеров граф, а одговарајући пут Ојлеров пут. Према томе: Ојлеров пут постоји ако и само ако постоји 0 или 2 непарна чвора графа. У свим осталим случајевима, тј. кад је број чворова непарног степена различит од 0 и 2, граф се не може нацртати.
Ако су сви чворови графа парног степена (0 непарних чворова), он се може нацртати и то полазећи из било којег чвора графа, а завршавајући у истом чвору. У случају да постоје два чвора непарног степена, граф се може нацртати полазећи од једног од тих чворова, а завршавајући у другом.
Граф (мрежа) дат на слици 5 има 8 непарних чворова и, према томе, не може се трасирати без подизања оловке. Слика 4 приказује „кенигсбершки мултиграф”, где су острва и обале представљени чворовима, а мостови гранама. Он има 4 чвора непарног степена и, на основу Ојлерове теореме, то није Ојлеров граф. Према томе, жељени пут преко 7 кенигсбершких мостова не може се реализовати.
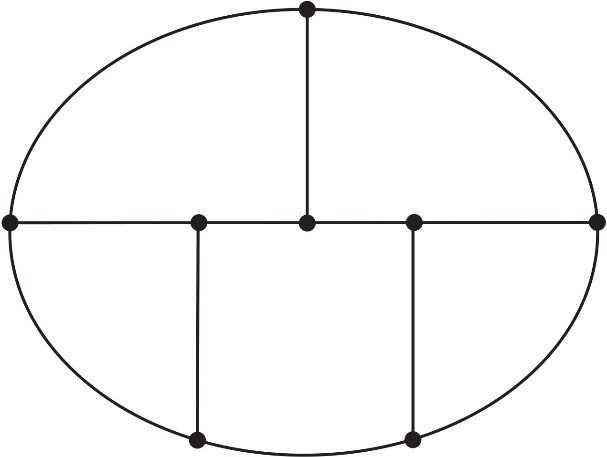
Сл. 5 Цртање раванске мреже
Kао додатни задатак у вези с применом Ојлерове теореме, дајемо следећи проблем чији је аутор он сам, а који је сличан прелазу преко кенигсбершких мостова али знатно компликованији; овде се захтева прелазак преко 15 мостова: Четири острва А, B, C и D повезана су помоћу 15 мостова са обалама реке и између себе, као што је приказано на слици 6. Да ли је могуће обићи све мостове прелазећи преко сваког моста једном и само једном?
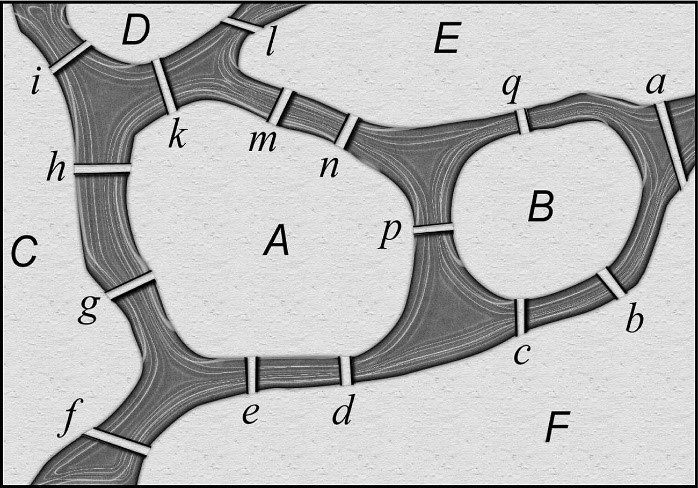
Сл. 6 Ојлеров задатак о прелазу преко
15 мостова
За читаоце који немају времена (или стрпљења) за решавање овог задатка, у наставку дајемо решење. Да бисмо решили проблем, представимо четири острва А, B, C, D и обале Е и F помоћу чворова графа, а мостове гранама (означених малим словима), видети слику 6. Kао што се види са слике 7, граф има два чвора непарног степена (deg(D) = 3, deg(E) = 5). С обзиром на горе формулисну Ојлерову теорему постоји захтевани пут преко свих 15 мостова који полази од чвора D и завршава у чвору Е, или обратно.
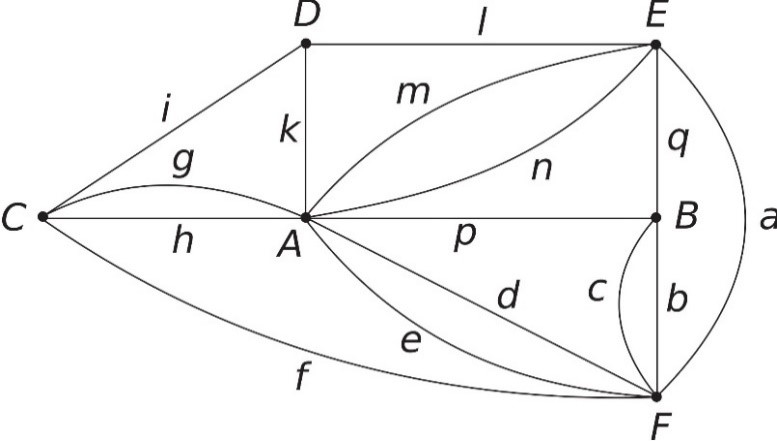
Сл. 7 Граф Ојлерових 15 мостова
Прелаз се може извршити, на пример, у поретку (решење није једнозначно)
E a F b B c F d A e F f C g A h C и D k A m E n A p B q E l D
или у обратном поретку полазећи од тачке D и завршавајући у Е.
Задатак за радознале и врло упорне: Одредити сва решења!








