У геометрији Пикова теорема даје врло једноставну формулу за израчунавање површине простог полигона (полигона који нема „рупа” и чије се странице не секу), чија су темена задата целобројним координатама. Израчунавање се своди на пребројавање тачака у унутрашњости полигона и на његовим границама. У прилогу су дате две интересантне примене Пикове теореме.

Проф. др Миодраг Петковић
Нацртајмо на листу папира вертикалне и хоризонталне линије тако да образују мрежу једнаких квадрата са страницом 1. Узмимо затим темена квадрата за темена полигона чије се странице не пресецају, као на слици 1. Пикова теорема нам каже да се површина А овог полигона може израчунати пребројавањем броја U тачака које се налазе унутар полигона и броја G тачака које формирају границу полигона на следећи начин: A = U + G/2 – 1. Британски писац Дејвид Дарлинг написао је да „Пикова теорема представља везу између традиционалне еуклидске геометрије и модерне дигиталне (дискретне) геометрије”.
Ако је страница квадрата једнака а, лако се показује да је површина једнака
A = (U + G/2 – 1) S= (U + G/2 – 1) a2, где је S површина квадрата из поменуте мреже.
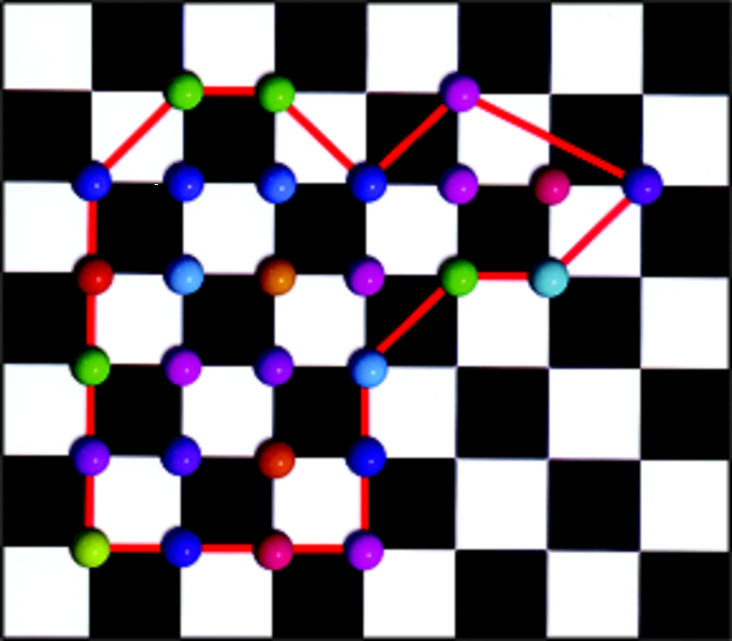
Сл. 1 Илустрација Пикове теореме
Аустријски математичар Георг Пик (Pick, 1859-1942) формулисао је ову теорему 1899. Пик је познат и по томе што је упознао Алберта Ајнштајна са математичарима који су му помогли (у математичком делу) у раду на општој теорији релативности. Нажалост, Пик је доживео трагичну судбину. Будући да је био Јеврејин, пред Хитлеровом окупацијом Аустрије 1938. побегао је у Праг, али је после окупације Чехословачке био ухапшен и послат у концентрациони логор Терезинштад, где је умро 1942.
Kористећи папир са описаном квадратном мрежом, можемо применити Пикову теорему да проценимо површину региона (рецимо државе), ако његове границе апроксимирамо помоћу полигона. Наравно, уколико је мрежа гушћа, резултат ће бити тачнији. На слици 2 полигоном су приближно ограничене границе америчке савезне државе Тексас. У овом случају избројали смо U = 101, G = 52, док је ивица квадрата мреже око а = 72 километара. Kратка рачуница даје површину Тексаса
P = (U + G/2 – 1) x 722 = 126 x 5184=653 184 km2.
Тачна површина је PT=696 240 km2, што значи да је начињена грешка од око 6,6\%.
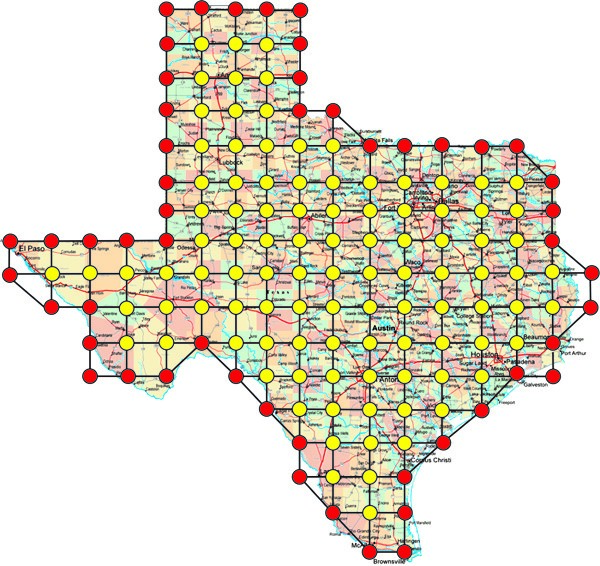
Сл. 2 Израчунавање површине Тексаса
Пикова теорема може се искористити у решавању једног интересантног задатка који се односи на затворени скакачев пут. То је затворени непресецајући пут састављен од потеза скакача на шаховској табли. Доказати да је површина окружена затвореним скакачевим путем целобројни умножак површине једног квадрата шаховске табле n x n (n > 3).
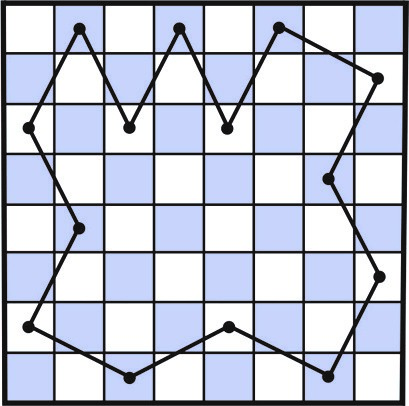
Сл. 3 Површина ограђена затвореним скакачевим путем
Решење: Нека је С површина квадрата шаховске табле димензије n x n. Примењујући Пикову формулу A = (U + G/2 – 1) S, довољно је показати да је U + G/2 – 1 цео број, а то ће бити ако је G паран број. Пошто се скакачев пут састоји наизменично од белих (b) и црних поља (c), у случају било ког затвореног пута (полазно поље је и завршно) лако је запазити да је број поља преко којих је прешао скакач увек паран. Заиста, низ c (почетак) – b – c – b – \cdots – c -b – c (крај), придружен затвореном скакачевом путу, увек има паран број потеза; видети слику 3. Kако је број квадрата који припадају затвореном скакачевом путу једнак броју граничних тачака G, доказ је комплетиран.
Додајмо још да са слике 3 налазимо да је U = 34, G = 14, одакле на основу Пикове теореме следи да је површина ограничена затвореном путањом скакача у овом конкретном примеру једнака A = 34 + 14/2 – 1 = 40.








