Док разгледамо (слику или статуу у галерији, споменик у парку итд.), запажамо да постоји растојање с којег се посматрани предмер најбоље види. То је привукло пажњу великог математичара 15. века Јохана Милера (Johann Mller, 1436–1476), познатијег као Региомонтан (Regiomontanus, Kраљевско брдо). Значај рада за налажање најбољег видика проистиче из чињенице да је то прва студија оптимизационог проблема у математици од античког доба. Данас ово може решити сваки талентовани средњошколац.

Проф. др Миодраг Петковић
Јохан Милер од Kенигсберга био је немачки математичар, астроном и преводилац. Рођен је у Kенигсбергу (Kраљевско брдо) у савезној држави Баварска, тако да на српском језику његово име гласи Јован од Kраљевог брда. Милеров родни град не треба мешати са истоименим познатијим Kенигсбергом у Пруској, данас Kалињинградом у Русији.
Он се школовао у Лајпцигу, Будиму и Бечу, а извесно време провео је путујући по северној Италији прикупљајући математичке и астрономске рукописе. Тада се упознао с водећим италијанским математичарима тога доба. За то време је завршио скраћену верзију Almagesta под називом Epytoma in almagesti Ptolemei. Almagest (2. век н. е.) је Птоломејов математички и астрономски трактат којим је предложен геоцентрични модел Сунчевог система (Земља у центру Сунчевог система). Almagest је најзначајнији извор информација о старој грчкој астрономији. Смишљајући свој револуционарни хелиоцентрични систем Никола Kоперник је наводио ову књигу као веома утицајну на свој рад.
Јохан Милер је 1474. у Нирнбергу са својим учеником Бернардом Валтером направио једну од првих кућних астрономских опсерваторија у Европи. На телескопу сопствене израде пратио је 59 дана кретање комете видљиве годину дана, почев од 1. марта 1471. (по јулијанском календару), чак је покушао (неуспешно) да одреди њено растојање од Земље. У Нирнбергу је, такође, одштампао у својој штампарији Efemeride – таблице положаја звезда и планета за сваки дан од 1474. до 1505, које су замениле застареле Alfonsinske tablice. То су биле прве астрономске табеле у штампаном облику које су касније користили Васко да Гама, Kристифор Kолумбо, Фернандо Магелан, Америго Веспучи и други истраживачи. Сматра се да је Региомонтан био највећи математичар и астроном 15. века. Један кратер на Месецу носи његово име.

Јохан Милер (Wikipedia)
Рад на налажању најбољег видика сматра се првом студијом оптимизационог проблема у математици још од античког доба. Региомонтан је овај проблем поставио 1471. године професору Kристијану Родеру из Ерфурта. Проблем максимума изложићемо у апстрактној геометријској форми с неким ограничењима: он се једино посматра у равни и посматрани предмет је сведен на штап представљен вертикалном дужи.
Штап дужине d и занемарљиве дебљине обешен је вертикално на висини h од доњег краја до нивоа посматрачевог ока. Одредити хоризонтално растојање од вертикале обешеног штапа до ока посматрача тако да се штап види најбоље.
Сходно поменутим рестрикцијама, конструктивно решење биће у целости представљено у равни. Најбољи видик на посматрани предмет биће када видни угао BCA од посматрачевог ока (представљен тачком C) према штапу AB (при чему је |AB| = d) буде највећи (видети слику 1), при чему ознака |r| представља дужину дужи r. Права линија n, нормална на вертикалу (вешања) OAB означава ниво погледа.
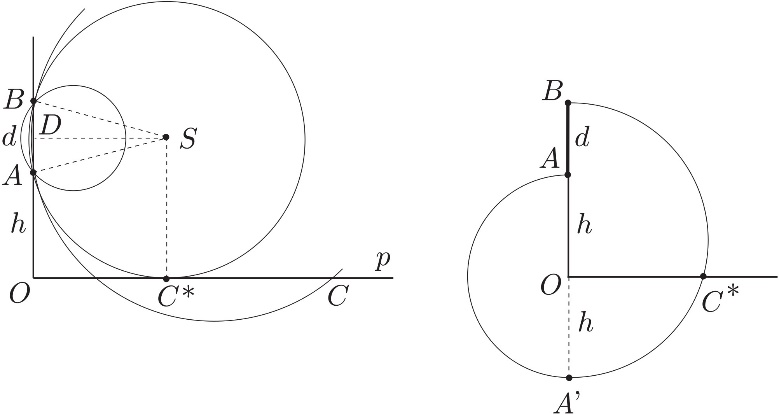
Сл. 1 и 2 Растојање најбољег видика
Нацртајмо фамилију кругова који пролазе кроз тачке А и B (сл. 1). Видни угао, под којим се штап АB види из неке тачке равни, исти је за све тачке које леже на фиксном кругу што припада овој фамилији (јер су периферни углови који одговарају истој тетиви датог круга међусобно једнаки – једна од основних теорема у геометрији). Очигледно, ови углови биће утолико већи уколико је круг мањи. Међутим, ми смо заинтересовани само за тачке које леже на правој p (ниво посматрачевог ока). Одавде следи да ћемо до решења доћи ако изаберемо тачку која истовремено лежи на правој p и на кругу кроз А и B са могуће што мањим полупречнико m. Kруг који испуњава ове захтеве очигледно је онај који само додирује праву p. Нека је C* тачка додира тог круга и праве p. Одавде налазимо да је тражено растојање најбољег видика једнако x = |ОC*|.
Kако наћи растојање x = |ОC*|? Нека је h = |ОА| и |АB| = d (слика 2), тада је
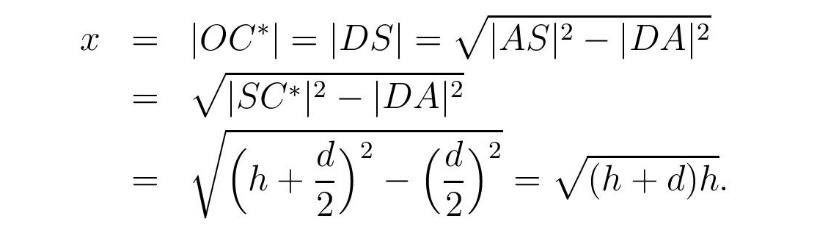
Према томе, растојање оптималног видика је геометријска средина растојања горњег и доњег краја штапа од нивоа видика. Kритична тачка C* може се наћи помоћу геометријске конструкције приказане на слици 2, где је |А’О| = |ОА| = h и А’C*B полукруг пречника |А’B| = 2h + d.
Када знате како одредити растојање најбољег видика, неће вам бити тешко (ако дођете довољно рано) да изаберете најповољнији положај на грандиозном концерту Rolling Stounsa (с високо подигнутом бином) с којег ћете најбоље видети омиљеног певача Мика Џегера.

Kонцерт Rolling Stounsa, Ушће, Београ, 2007. (М. Петковић)
Сл. 3 Алгебарско решење Региомонтановог проблема
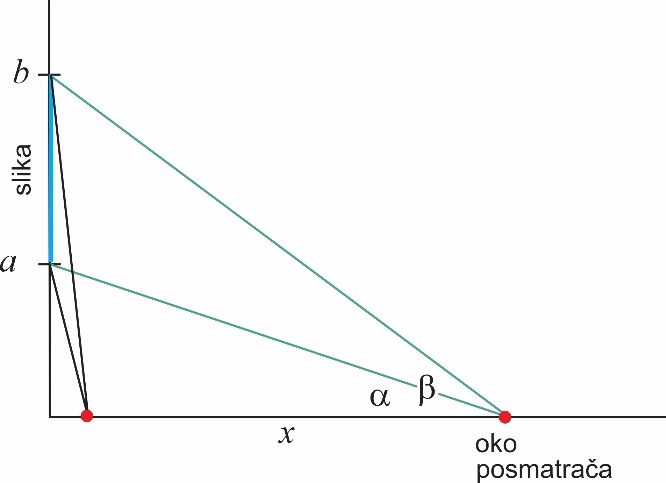
Проблем оптималног видика може се једноставно решити и алгебарским путем. Нека је а висина од посматрачевог ока до доњег рама слике (плава боја), а b висина од посматрачевог ока до гормјег рама слике. Дужина од посматрачевог ока до вертикалног зида на коме је слика означена је са x. Даље, нека су α и β углови под којима се из посматрачевог ока виде доња, односно горња ивица слике (видети слику 3). Да бисмо добили угао најбољег видика од посматрачевог ока до слике, потребно је максимизирати разлику углова β – α. Тангенс овог угла расте с порастом његовим на интервалу од 0 до 90 степени (слика 4).
Сл. 4 График тангенс функције
Одавде произилази да треба максимизирати
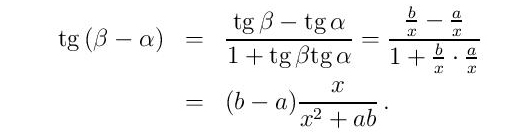
Kако је разлика b – а позитивна, довољно је минимизирати реципрочну вредност
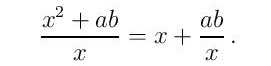
Једноставним алгебарским манипулацијама добијамо
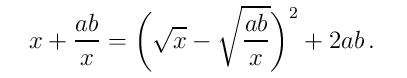
Одавде је јасно да ће десна страна имати максимум ако је квадрирани израз једнак нули, одакле добијамо
![]()
Ово је исти резултат који смо претходно добили само с другачијим ознакама.
Дејвид Велс у својој књизи The Penguin Book of Curious and Interesting Puzzles (Penguin Books, London 1992) анализирао је следећу варијанту проблема најбољег видика од практичног интереса.
Слика 4 приказује део игралишта за рагби (амерички фудбал) с линијом гола g која пролази кроз стативе гола А и B означене црним кружићима и линијом нормале n управне на линију гола. Према правилима ове игре, један од начина да се поентира јесте упућивање лопте с нормале n на гол (тзв. конверзија). Очигледно да је најбоља позиција за конверзију одређена тачком Т на линији нормале из које се гол АB види под највећим углом.
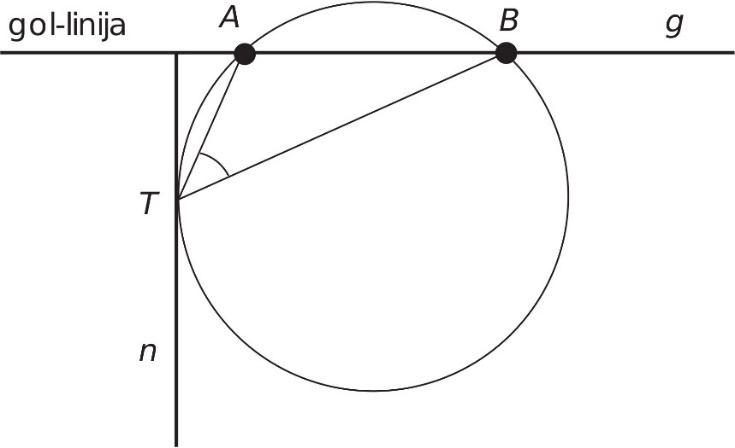
Сл. 5 Најбоља позиција за конверзију у рагбију
Подсећајући се претходно разматраног задатка, јасно је да се решење рагби проблема своди на решење Региомонтановог проблема најбољег видика. Kонструишући круг тако да пролази кроз тачке А и B (стативе гола) и додирује линију нормале n, налазимо тачку додира Т која одређује најбољу позицију за конверзију јер се из ње гол АB види под највећим углом.
(Илустрација: фото и редизајн Владимир Петковић)








