Осим круга, најједноставнија затворена крива константног дијаметра и има облик „криволинијског троугла”. Због својих необичних особина нашао је примену у различитим дисциплинама, почев од архитектуре, бушења квадратних рупа, конструкције мотора за разне намене (покретање аутомобила, авиона, водених скутера), аутоматских робота-усисивача, па све до трзалица за гитаре.

Проф. др Миодраг Петковић
Повремено ће се у овој рубрици у појављивати занимљиви прилози из света математике који укључују интересантне математичке формуле, догађаје из света математике и живота великих математичара и елементарне али интригантне и изазовне задатке за чије решавање је довољно средњошколско знање математике. Већина ових прилога, као и још математичких прича и занимљивости може се наћи на сајту www.miodragpetkovic.com аутора ових прилога (опције теме у менију).
Прилог почињемо малим подсетником из геометрије: за фигуру у равни каже се да је конвексна ако дуж која спаја било које две тачке A и B ове фигуре такође припада овој фигури. Kруг, елипса, квадрат и троугао су примери ограничених конвексних фигура у равни. Сада је лакше схватитити како се у геометрији дефинишу конвексне фигуре константног дијаметра, које су главна тема овог прилога. Поједностављено, то су фигуре код којих је растојање између произвољног пара паралелних „носећих правих” (две праве истог нагиба које обе додирују контуру фигуре без пресека) константно, без обзира на оријентацију ових правих. У литератури се често уместо термина дијаметар колоквијално користи термин „ширина”.
Ако посматрамо фигуру S на слици 1 видимо да нормална растојања Da и Db, која одговарају правцима дефинисаним векторима a и b, нису једнака и фигура S није фигура константне ширине. На слици 2 је приказана фигура константне ширине и то управо Релоов троугао, о коме ће надаље бити речи. Чувени математичар Леонард Ојлер био је први који је открио постојање поменутих фигура о којима је писао у свом раду из 1781.
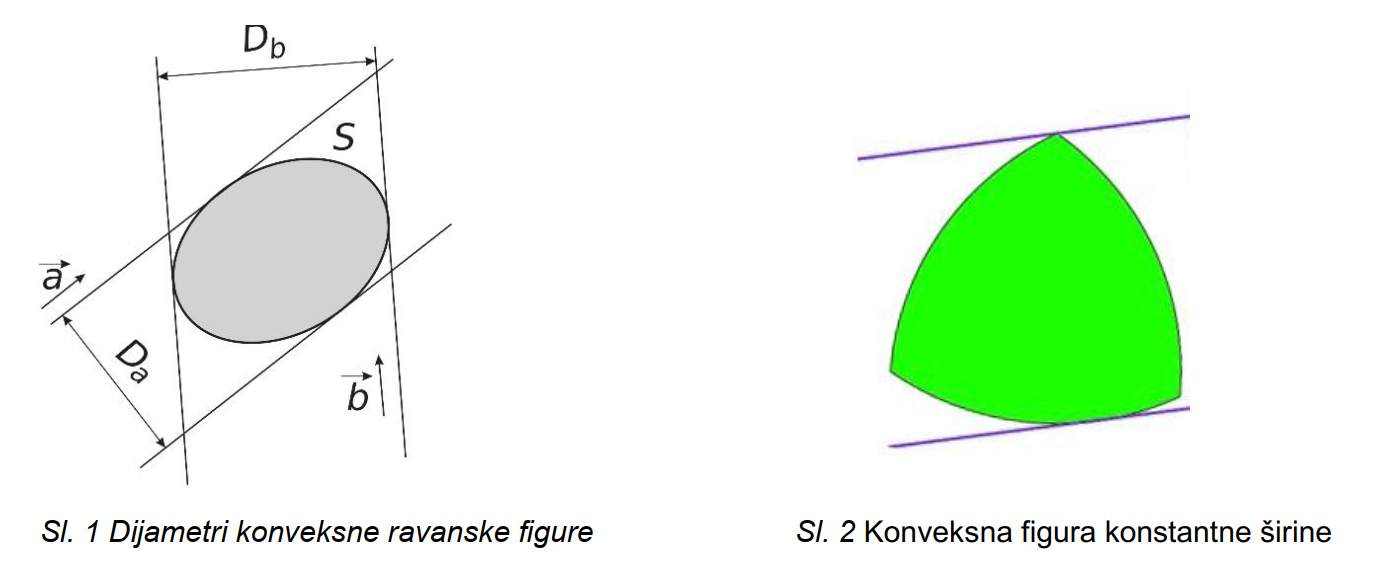
Да ли је круг једина затворена крива у равни са константним дијаметром? На ово питање већина људи ће одговорити потврдно, што је нетачно. Постоји бесконачно много затворених кривих константног дијаметра.
Непрепознавање таквих кривих имало је штетне последице у пракси, нарочито у индустрији обраде материјала.
Изузимајући круг, најједноставнија затворена крива константног дијаметра јесте Релоов троугао, по имену немачког инжењера и математичара Франца Релоа (F. Reuleauh, 1829-1905) који је доста радио на практичним применама Релоовог троугла. Овај „криволинијски троугао” добија се када се из темена једнакостраничног троугла ABC опишу кружни лукови полупречника једнаког страници троугла (сл. 3а). Очигледно је да овако конструисан (Релоов) троугао мора имати константан дијаметар једнак страници троугла ABC.
С обзиром да Релоов троугао (скраћено RT) има константан дијаметар, његова контура је ограничена паром паралелних линија које се секу под правим углом. На тај начин ове четири праве формирају квадрат, одакле произилази да се Релоов троугао може окретати унутар квадрата странице једнаке дијаметру троугла. При овој ротацији RT у сваком тренутку остварује контакт са све четири странице квадрата (сл. 3б). Сваки „угао” троугла описује путању која је скоро квадратног облика, са малим заобљењима у угловима квадрата. Ова особина дала је идеју енглеском инжењеру Харију Ватсу да 1914. године конструише ротирајућу бургију која је могла да буши рупе квадратног облика! Ватсова бушилица приказана је на сл. 4. Бушење је обезбеђено одговарајућим вођењем бушилице. Попречни пресек бургије је, у ствари, Релоов троугао на коме су, да би се начиниле ивице за сечење и рендисање, направљена три удубљења.
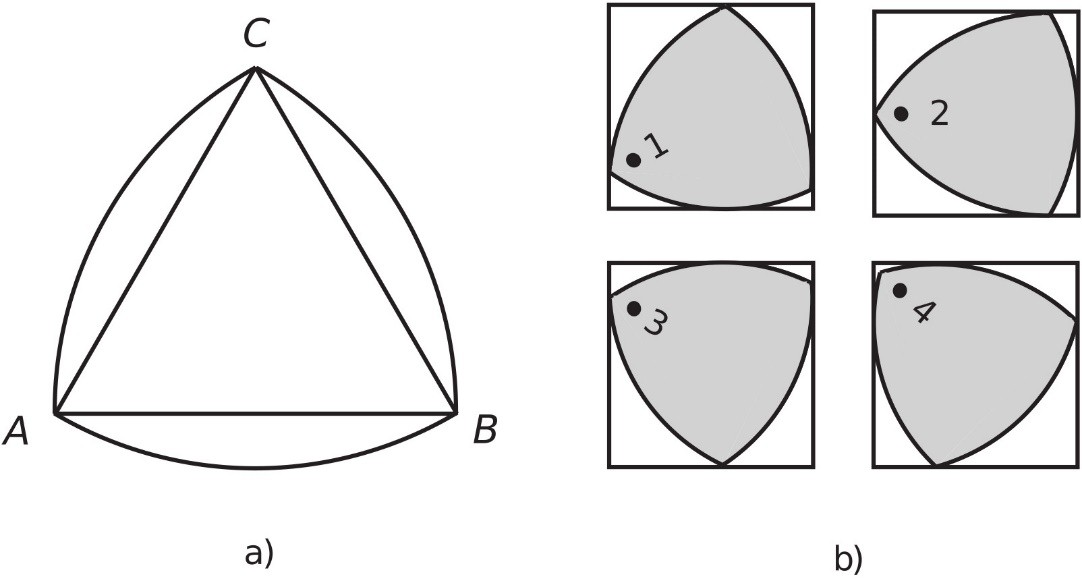
Сл. 3 Релоов троугао
Све раванске фигуре истог дијаметра d, укључујући и Релоов троугао, имају једнаке обиме (следи на основу Барбиерове теореме). С обзиром да овом скупу припада и круг, овај обим је једнак .
Поменимо и интересантну чињеницу да Релоов троугао има најмању површину у класи фигура константног дијаметра d (следи на основу Блашке-Лебегове теореме). Ова површина је једнака
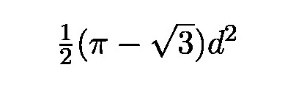
а површина избушена помоћу RT покрива приближно 98,77% површине стварног квадрата. Ова мала разлика јавља се јер RT ствара врло мала заобљења у угловима квадрата због тога што је „угао” Релоовог троугла исувуше „туп”. Он, наиме, износи 120 степени што је, с друге стране, идеално ако желимо да избушимо шестоугаони отвор. Додајмо и ову интересантну чињеницу: од свих раванских фигура константног дијаметра d највећу могућу површину има круг површине
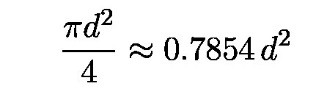

Сл. 4 Рело-Ватсова бушилица за бушење квадратних рупа
(Илустрација: В. Петковић)
Ево још неколико интересантних података о Релоовом троуглу:
● Читаоци који су мање-више упознати са типовима мотора код аутомобила сигурно су чули за Ванкелов мотор. Kонструисао га је немачки инжењер Феликс Ванкел, а прототип је завршен 1957. То је врста мотора са унутрашњим сагоревањем који у свом „центру” има ексцентрични ротор по облику сличан Релоовом троуглу, али с мањом закривљеношћу (сл. 5). У поредењу са клипним мотором, Ванкелов мотор је компактнији и лакши за дату снагу, има мање вибрација и уравнотежено испоручује снагу и то при великом броју обртаја. Kористи се не само код аутомобила већ и за покретање авиона, водених скутера, моторних тестера итд.

Сл. 5 Ванкелов ротациони мотор (Starecated.com)
● Точак чији пресек има облик Релоовог троугла се може котрљати али није подесан за глатку вожњу јер његова оса „одскаче” горе и доле три пута за време једног окрета. Овај концепт био је искоришћен у научнофантастичној причи Three-Cornered Wheel Пола Андерсона (1963).
● Релоов троугао се користи у неким градовима (нпр, у Сан Франциску) као облик попречног пресека навртке вентила ватрогасног хидранта. Специфичан облик навртке отежава отварање хидранта помоћу стандардних кључева и кљешта и спречава ненаменска коришћења; ватрогасне хидранте могу да отварају једино ватрогасци који поседују специјални кључ.
● У математици постоји хипотеза да се од свих фигура константног дијаметра најгушће могу упаковати у равни управо Релоови троуглови. Индекс паковања се дефинише као однос G површина свих фигура упакованих у квадрат и површине тог квадрата чија страница тежи у бесконачност. Математичари су поставили хипотезу да је
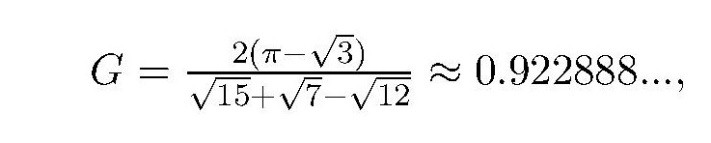
али још увек нема доказа.
● Аутоматски усисивач-робот RULO компаније Panasonic има облик заснован на Релоовом троуглу јер је то најефикаснији начин за чишћење прашине у угловима просторија.
● У готској архитектури 13. и 14. века, Релоов троугао био je један од неколико криволинијских облика који су се често користили за прозоре и друге архитектонске објекте и украсе. Kарактеристични су примери цркве Onze-Lieve-Vrouwekerku (Црква наше Госпође) у белгијском граду Брижу (сл. 6) и чувеној миланској катедрали Duomo. Попречни пресек зграде у Kелну (Немачка), познате као Kelnski trougao, доста подсећа на Релоов троугао, слика 7.

● Једна од најранијих примена Релоовог троугла је мапа света Леонарда да Винчија из 1514. године подељена у 8 октаната у облику Релоовог троугла (сл. 8).
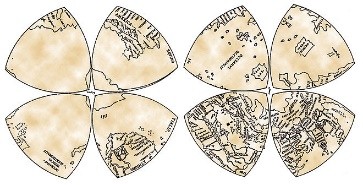
Сл. 8 Да Винчијева мапа света (Wikipedia)
● Од свих четвороуглова највећи однос обима и пречника (најдужег растојања између темена) има делтоид („змај”) једнаких дијагонала уписан у Релоов троугао (сл. 9).

● Пик (или у жаргону гитариста трзалица) за свирање гитаре је најчешћi облик који подсећа на Релоов троугао (сл. 10). Узгред, аутор овог прилога је фотографисао оригиналну трзалицу чувеног гитаристе Ерика Kлептона у Hard Rock кафеу у Бостону. Гитаристима добро дође његов ергономски и симетричан облик који природно тежи да заузме прави смер, тако да не морају да воде рачуна како га држе у руци. Осим тога, његова три једнака шиљка се теже хабају и имају дужи век трајања у поређењу, на пример, с троугластим пиком.
● Поводом неких свечаности и пригодних догађаја на Бермудима се издају серије кованица у облику Релоовог троугла (видети слику испод наслова) које се могу користити у аутомат-машинама.








