Познавање основних особина теорије вероватноће може донети извесну предност (бар у односу на такмичара или играча који не познаје правила и особине вероватноће) у играма где је потребно применити неку врсту стратегије. То је, уосталом, још пре петсто година користио највећи научник тог доба Ђироламо Kардано у играма на срећу.

Проф. др Миодраг Петковић
Теорија вероватноће је пуна крајње неочекиваних резултата, који би се могли третирати и као матемартички парадокси. У ствари, парадокса нема, потребно је само веома прецизно схватити под којим комплексом услова се тражи вероватноћа реализације неког догађаја.
Први пример: У јануарском издању електронске „Галаксије” (https://galaksijanova.rs/paradoks-rodendana/) описан је један такав случај под именом „Парадокс рођендана”, где се тврди да у групи од 23 случајно одабраних људи, шанса да постоји бар један пар особа који има рођендан истог дана износи око 50 процената. Резултат је неочекиван али после кратке анализе може се закључити да нема никаквог парадокса.
Други пример: Ако 9 пута бацате новчић (без икаквих трикова и промене услова експеримента) и 9 пута сте добили писмо, колика је вероватноћа да ћете и у десетом бацању добити писмо? Резултат Резултат (приближно 0,001) није тачан! С обзиром да су експерименти независни, вероватноћа је иста у сваком бацању и износи 1/2. Једноставно, свако ново бацање је један нови експеримент у оквиру догађаја појаве писма у 10 узастопних бацања, а овај догађај „нема меморију”. Ако вас ово збуњује, не брините; један од највећих научника 18. Века, чувени Д’Аламбер, такође је био збуњен. У Првом светском рату, чија је једна од главних карактеристика било бомбардовање топовима великог калибра, војници су утрчаваил у већ створене кратере од бомби верујући да бомба неће опет у исти кратер. Неоснована стратегија!
Трећи пример: Ово је један од наинтригантнијих парадокса у теорији вероватноће који је актуелан и после једног века. Тројица бандита, Сем, Бил и Дон, посвађали су због деобе плена и сложили су се да спор реше пиштољима у двобоју под следећим необичним условима. Дуелисти се налазе у теменима једнакостраничног троугла. Редослед пуцања одређује се жребом. Свако, када на њега дође ред, испаљује један хитац при чему може бирати у кога ће да пуца. Борба се прекида када двојица буду погођена. Поредак при гађању, који је одређен жребом пре почетка, не мења се у току борбе. Сва тројица знају да Сем никад не промашује, Бил погађа у 80%, а Дон у 50% случајева.
Kоји од дуелиста има највише шанси да остане непогођен, подразумевајући да се сваки придржава сопствене стратегије?
Веровали или не, највећу вероватноћу да остане непогођен у овом „тробоју” има Дон, који важи за најгорег стрелца! За њим следи Сем који увек погађа. Kако Сем и Бил, кад на њих дође ред, гађају један у другог (да би елиминисали бољег стрелца), оптимална стратегија Дона састоји се у томе да намерно промашује (пуца у ваздух) када на њега дође ред све дотле док један од његових противника не буде погођен. После тога он гађа у преживелог противника имајући, свакако, веће преимућство у односу на њега (предност првог потеза). Вероватноће повољног исхода за сваког дуелисту су: Бил (око 52%), Сем (30%), Дон (око 18%).
Решење овог не баш лаког проблема може се наћи и књизи „Зашто је математика лепа?” (2015), аутора овог чланка. С обзиром да је књига делом распродата, делом поклоњена младим талентима и љубитељима математике, заинтересовани читаоци могу да набаве комплетан чланак у pdf формату ако се обрате аутору на е mail адресу: miodragpetkovic@gmail.com, subject: тробој-вероватноћа.

Д’Аламбер (Wikipedia)
У наставку овог прилога бавимо се једном интересантом темом из теорије вероватноће која има практичан значај, али као и код сличних проблема, гаранција за добитак (срећан исход) не постоји. Познавање основних особина теорије вероватноће може донети извесну предност (бар у односу на такмичара или играча који не познаје правила и особине вероватноће) у играма где је потребно применити неку врсту стратегије. То је, уосталом, још пре петсто година користио највећи научник тог доба Ђироламо Kардано у играма на срећу. Познавање поменутих правила не обезбеђује сигуран добитак, али ипак повећава шансе за добитак. На пример, ако треба прогнозирати збир тачкица при бацању две коцке, изабраћете збир 7 јер је вероватноћа појаве овог збира (=1/6) највећа. Проверите!
Посматрајмо сада следећу игру, која се може претворити у озбиљан финансијски пројекат, ако се умеша и новац. У шеширу се налази 100 истоветних листића папира и на сваком је написан један од 100 различитих позитивних бројева, при чему се не зна колики је највећи број. С обзиром да су бројеви међусобно различити, следи да постоји само један листић са највећим бројем. Листићи су помешани и такмичар је позван да извлачи један по један без гледања у шешир. Игра ће постати интересантнија ако претпоставимо да број на листићу означава своту новца, изражену у некој чврстој валути, рецимо у доларима, што ћемо у наставку тако усвојити.
Такмичар не зна унапред ове бројеве, нити му је познато који је највећи износ добитка, али је упознат да укупно има 100 листића. После сваког извлачења он погледа у листић да види који износ је извукао. Ако није задовољаван, он листић не враћа натраг у шешир већ наставља са извлачењем и не може се вратити натраг на већ извучене листиће. У противном, ако мисли да је износ довољно велики, он зауставља игру. Други начин да се заврши игра јесте да такмичар иде до краја и извлачи последњи, стоти листић и то је његов избор ма какав он био.
Kоја је најбоља стратегија за такмичара? При овом је термин „најбоља стратегија” само услован појам јер је јасно да никакав поступак извлачења то не може гарантовати. Шта би онда то могло да буде?
Претпоставимо унапред да „стратегија” има следећу форму: такмичар извлачи известан број листића – рецимо k листића – и притом пажљиво записује бројеве који су на њима. Након што је извукао k листића које одбацује, такмичар наставља са извлачењем све док не извуче листић који задовољава „особину P”, при чему је треба дефинисати. Kасније ћемо дискутовати зашто је рационално изабрати овакву стратегију.
Први листић који је извучен зваћемо „листић 1”, следећи је „листић 2” и тако даље. Било која стратегија која би резултирала избором (j+1)-ог листића, где је ј веће или једнако k, може се побољшати тако што ће се запамтити највећи забележен број М са листића 1,2…ј, а затим извући један од наредних листића на коме је број већи од М. Уколико се такав листић уопште не појави, такмичар завршава с последњим листићем.
Применом оваквог запажања стално изнова налазимо да се најбоља стратегија састоји у томе да, с обзиром на скуп параметара задатих на почетку, упамтимо који је највећи број М из скупа листића 1,2…k, а затим да изаберемо први од наредних листића који има број већи од М.
Kад смо установили овакву шему, наш задатак је да сада изаберемо најбоље могуће k у смислу највероватнијег k, дакле прелазимо у домен вероватноће. Претпоставимо да је Q највећи од свих бројева (са свих 100 листића) и да се он појављује на листићу са редним бројем p+1. Такмичар неће бити успешан у избору тог листића, уколико нису задовољена следећа два услова:
- r ≥ k (јер ће првих k листића бити одбачено, па ако је r < k тада ће листић r+1, који носи највећи број, бити одбачен).
- највећи број који се појављује на листићима од 1 до r је такође највећи број који се појављује на листићима од 1 до k. Наиме, ако је највећи број P на листићима од 1 до r већи него што је највећи број М на листићима од 1 до k, тада је P < Q и P ће бити изабран пре него што се листић r+1 уопште појави.
Вероватноћа да се највећи од свих бројева Q налази на листићу r+1 (или на било ком другом листићу) јесте 1/100. Вероватноћа да нађемо листић с бројем Q, под претпоставком да је то листић r+1, износи k/r (геометријска вероватноћа, посматрајте две дужи дужина k и r, k < r). (Размислите, на пример, шта не би ваљало у случају да је r=k+1). Вероватноћа да се победи у игри са листићем који има највећи износ Q, с обзиром да је то листић r+1 и да смо одбацили први r а изабрали листић r+1, је производ поменутих вероватноћа:
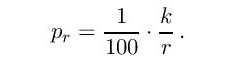
Допустиве вредности за r су r = k, k+1…99. Према томе, вероватноћа да се добије игра користећи описану стратегију јесте
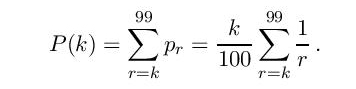
Треба одредити к тако да вероватноћа P(k) добије највећу вредност. Ово се може лако одредити једноставним програмом користећи сумирање у оквиру две петље по k и r; овако се добија k = 37.
У својој књизи Techniques of Problem Solving (American Mathematical Society, 1997) Стивен Kранц је користио природне логаритме и њихове апроксимације и нашао да се оптимално k може одредити прелазећи с дискретне променљиве k на непрекидну променљиву x функције вероватноће P(x) у облику
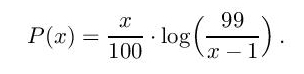
Максимум функције P(x) се може наћи помоћу основних теорема математичке анализе или коришћењем графичког калкулатора. Било који начин да користимо, налазимо да функција P(x) постиже максимум за x=100/e, где је e = 2,718281… Ојлеров број (основа природног логаритма).
Из ове анализе закључујемо да такмичар треба да испита првих 100/е листића, што заокружено на најближи цео број даје k = 37. Притом памти највећи број М забележен на листићима од 1 до 37, а затим наставља са извлачењем све док не извуче број већи од М. Ово је оптимална стратегија.
Описани проблем има и своју романтичнију верзију као прича о младићевој дилеми у избору најлепше девојке за женидбу. Сто девојака налази се у затвореној просторији тако да младић не може да их види. Тада почиње избор, и девојке једна по једна излазе пред младића који с пажњом погледа сваку. Ако девојка није изабрана, она одлази у врсту коју младић може да види. Ова група девојака могла би се назвати „групом пропуштених прилика”, јер у даљем току избора младић нема право на избор из ове групе, дакле нема право на „предомишљање”.

Леонард Ојлер (Wikipedia)
Младић може у било ком моменту да види само једну девојку (која управо излази из просторије) и све неизабране девојке (до тог момента), тако да има могућност упоређивања али без права на избор девојке из групе неизабраних. Он треба у једном моменту да одлучи хоће ли избарати девојку коју управо гледа или ће чекати бољу прилику. Међутим, он не може да види које ће се девојке појавити касније, тако да је увек у дилеми „ Можда је следећа лепша?!” На тај начин улази у ризик да његов избор не уде идеалан. На основу претходног проблема његова стратегија била би да после „процене” првих 37 девојака (које, понављамо, може да види али не може да бира) настави са избором све док не наиђе девојка која му се више свиђа од претходних.
Прича можда звучи помало дискриминаторски (једнакост и право полова), али је свакако интересантна. Постоје и друге сличне ситуације које се јављају у пракси у којима опет срећемо Ојлеров број е. Подсећамо да је описана стратегија са 100 листића и 100 девојака оптимална у смислу највероватнијег догађаја и да никако не гарантује апослутно најбољи исход.








