Добро је познато да је бинарни бројни систем нашао своју најкориснију примену при конструкцији дигиталних рачунара. Међутим, бинарни бројеви се, такође, користе у бројним ситуацијама где се јављају два стања, укључено/искључено, тачно/нетачно, ради/не ради итд. У овом прилогу биће приказана примена бинарних бројева за креирање стратегије добитка код једне од најстаријих и најзанимљивијих математичких игара за две особе, познате под именом ним.
Проф. др Миодраг Петковић
Једна од најстаријих и најзанимљивијих математичких игара за две особе је „ним”, за коју се претпоставља да потиче из Kине. Најпознатија и најраспрострањенија варијанта игра се са 12 фигура распоређених у три реда као на слици 1, али и произвољни распореди (с малим ограничењима) су допустиви јер је стратегија добитка у игри иста.
Правила „нима” су врло једноставна. Играч на потезу узима једну или више фигура (а може и све), али само из једног реда. Изгубио је играч који је узео последњу фигуру.
Због разних комбинација у распореду фигура, а нарочито ако има много редова и много фигура, на први поглед изгледа да је тешко пронаћи праву стратегију за играче у овој игри. Међутим, изненађујуће је да постоји једноставна добитна стратегија заснована на коришћењу бинарног бројног система. Ова стратегија омогућује, у зависности од почетног распореда фигура, победу једног од играча без обзира на игру противника. Детаљну анализу и доказ о егзистенцији оптималне стратегије први је дао Чарлс Бутон, професор математике на Хардварском универзитету (1901.). Он је и дао овој игри име „ним” (Nim) од старог облика енглеског глагола који је имао значење „украсти” или „скинути”.
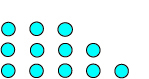
Сл. 1 „ним” (3,4,5)
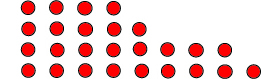
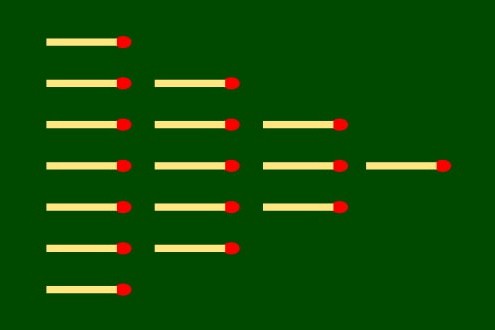
Сл. 2 „ним” (4,5,8,9)
Сваку комбинацију фигура (тренутну позицију) Бутон је назвао или „опасном” или „безопасном”. Ако играчу на потезу, који је упознат са оптималном стратегијом, тренутна позиција гарантује победу, она се назива безопасном или добијеном (скраћено ДП – добијена позиција), у противном је опасна или изгубљена (скраћено ИП – изгубљена позиција). „Ним” поседује особину да се из ДП може прећи у ИП или ДП, али из ИП било који потез води у ДП (за противника). Описана ситуација и омогућује добитну стратегију која се састоји у налажењу одговарајућег потеза (не увек јединственог) који своју ДП преводи у противничку ИП.
Изложићемо сада критеријум за ДП који је дао Чарлс Бутон. Нека је дата почетна позиција 𝑃 = (𝑛1, 𝑛2 … 𝑛p), где 𝑛i означава број фигура у i-том реду. Напишимо сваки од бројева у бинарном систему, рецимо 11 = (1011)2, а затим нађимо збирове одговарајућих цифара (које се налазе на истим позицијама, дакле у истим колонама) свих p бинарних бројева, вршећи сабирање у децималном систему. Нека највећи од бројева 𝑛i има k цифара у бинарном систему, тада ћемо имати суме 𝑆1, … 𝑆k (видети табелу 1). Небитно је да ли се суме означавају с лева на десно, или у обрнутом реду. За почетну позицију P = (3,4,5) имамо 𝑆1 = 2, 𝑆2 = 1, 𝑆3 = 2 (табела 1).

Табела 1: позиција (3,4,5) је непарна
Бутонов критеријум за безопасну позицију ДП гласи: позиција P је безопасна ако и само ако је бар један од бројева 𝑆1 непаран.
На основу овог, критеријум за опасну позицију може се исказати и на следећи начин: позиција P је опасна ако и само ако су сви збирови 𝑆1 парни бројеви.
Напоменимо да се у исказаним критеријумима нула сматра парним бројем.
Обично се позиција за коју су сви збирови 𝑆1 парни назива парном, у противном је непарна. У складу са претходним, парне позиције су опасне (ИП) за играча на потезу, док су непарне безопасне (ДП).
Добитна стратегија играча који има ДП заснива се на следећим тврђењима доказаним, нпр. у књизи Х. Штајнхауза One Hundred Problems in Elementary Mathematics (Dover Publication, 2016):
(i) Ако је позиција П парна, било који потез доводи до непарне (ДП) позиције.
(ii) Ако је позиција П непарна, увек постоји потез који доводи до парне (ИП) позиције.
Играч који има непарну (безопасну) позицију, своју добитну стратегију спроводи помоћу потеза којим непарну позицију преводи у парну (према ii такав потез увек постоји). Његов противник не може преокренути игру у своју корист јер било који његов потез доводи до непарне позиције (тврђење i).
Анализирајмо следећа два примера користећи горње критеријуме.
Пример 1. Посматрајмо почетну позицију P = (3,4,5) дату на слици 1. Овој позицији одговара табела 1 из које видимо да је непарна. То значи да у класичној поставци игре „ним” (3,4,5) играч који почиње игру увек добија партију ако до краја игре проналази потезе којим непарну позицију увек преводи у парну. С обзиром да је једино 𝑆2 = 1 непарно, довољно је из првог реда који садржи 3 фигуре узети 2 фигуре и од броја (11)2 = 3 (11) направити број (01)2=1. На тај начин добијају се суме 𝑆1 = 2, 𝑆2 = 0, 𝑆3 = 2 и играч на потезу има парну (ИП) позицију.
Дајемо пример игре између играча А и B за почетну позицију P = (3,4,5) (слика 1).
А: Узима две фигуре из првог реда. Добија се позиција (1,4,5) са сумама (2,0,2).
B: Узима једну фигуру из 2. реда (позиција (1,3,5), суме (1,1,3).
А: Узима три фигуре из 3. реда (позиција (1,3,2), суме (2,2)
B: Узима једну фигуру из првог реда (позиција (3,2), суме (2,1).
А: Узима једну фигуру из реда где су три фигуре (позиција (2,2), суме (2,0).
Овде би играч B могао да преда партију: ако узме једну фигуру, А узима две, ако узме две, А узима једну: у оба случаја остаје само једна фигура за губитника B. Партија се може представити и помоћу следећих слика, где бели кругови означавају узете фигуре.
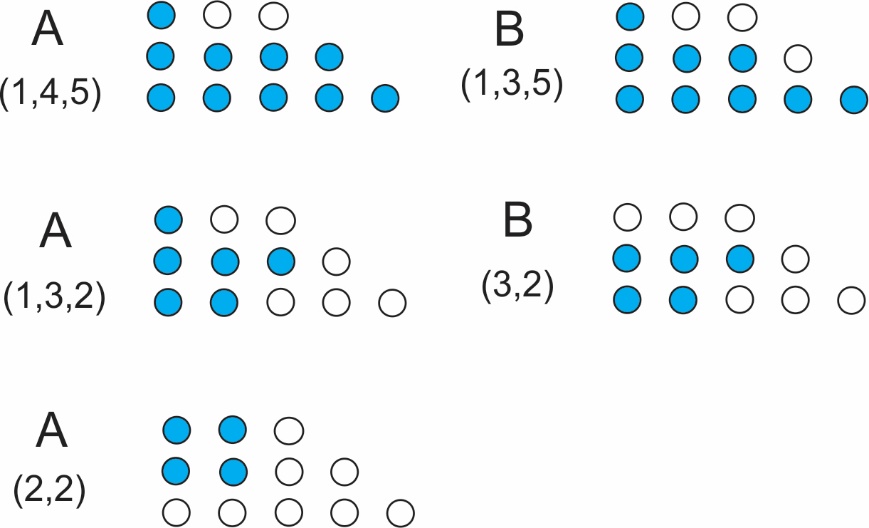
Пример 2. За поставку нима са слике 2 имамо P = (4,5,8,9) и на описани начин формирамо бинарну табелу 2.
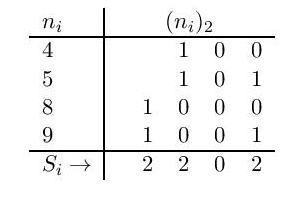
Табела 2: позиција (4,5,8,9)
Из пабеле 2 се види да је позиција парна (опасна). Играч који је на потезу губи партију, уколико је његов противник упознат са стратегијом добитка.
Приметимо да се игре у којима постоји добитна стратегија у зависности од распореда фигура и од тога који играч повлачи први потез сврставају у категорију нефер игара. Међутим, оваква категоризација није утицала на то да „ним” деценијама остане популарна игра, чак је једна партија виђена у филму L’anné dernière à Marienbad (Последња година у Маријенбаду), режисера Алена Ренеа из 1961. (Марјенбад, назив познате бање у Чешкој на немачком језику, на чешком Маријанске Лазње).








Da li je šah „fer“ igra?
Pitanje je koliko zanimljivo toliko i staro, po prvi put se javlja krajem 18. veka. Zavisno od broja uzoraka i primenjene statističke metodologije, Beli ima prednost koja procentualno iznosi između 52 i 56%. Ovo se ne odnosi na početnike i brzopotezne partije već na vrlo renomirane profesionalce sa približno jednakim ELO rejtingom, a takođe i na kompjutere približno istih karakteritika u standardnoj partiji. Proizilazi da je šah skoro fer igra (ishod je najbiži remiju), što je i mišljenje bivših prvaka sveta Kapablanke, Laskera, Fišera i Kasparova. Više o ovoj interesantnoj temi može se naći na Wikipediji (First-move advantage in chess).