Dobro je poznato da je binarni brojni sistem našao svoju najkorisniju primenu pri konstrukciji digitalnih računara. Međutim, binarni brojevi se, takođe, koriste u brojnim situacijama gde se javljaju dva stanja, uključeno/isključeno, tačno/netačno, radi/ne radi itd. U ovom prilogu biće prikazana primena binarnih brojeva za kreiranje strategije dobitka kod jedne od najstarijih i najzanimljivijih matematičkih igara za dve osobe, poznate pod imenom nim.
Prof. dr Miodrag Petković
Jedna od najstarijih i najzanimljivijih matematičkih igara za dve osobe je „nim”, za koju se pretpostavlja da potiče iz Kine. Najpoznatija i najrasprostranjenija varijanta igra se sa 12 figura raspoređenih u tri reda kao na slici 1, ali i proizvoljni rasporedi (s malim ograničenjima) su dopustivi jer je strategija dobitka u igri ista.
Pravila „nima” su vrlo jednostavna. Igrač na potezu uzima jednu ili više figura (a može i sve), ali samo iz jednog reda. Izgubio je igrač koji je uzeo poslednju figuru.
Zbog raznih kombinacija u rasporedu figura, a naročito ako ima mnogo redova i mnogo figura, na prvi pogled izgleda da je teško pronaći pravu strategiju za igrače u ovoj igri. Međutim, iznenađujuće je da postoji jednostavna dobitna strategija zasnovana na korišćenju binarnog brojnog sistema. Ova strategija omogućuje, u zavisnosti od početnog rasporeda figura, pobedu jednog od igrača bez obzira na igru protivnika. Detaljnu analizu i dokaz o egzistenciji optimalne strategije prvi je dao Čarls Buton, profesor matematike na Hardvarskom univerzitetu (1901.). On je i dao ovoj igri ime „nim”(Nim) od starog oblika engleskog glagola koji je imao značenje „ukrasti” ili „skinuti”.
Sl. 1 „nim” (3,4,5)
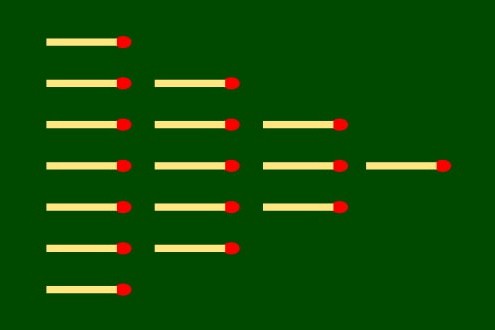
Sl. 2 „nim” (4,5,8,9)
Svaku kombinaciju figura (trenutnu poziciju) Buton je nazvao ili „opasnom” ili „bezopasnom”. Ako igraču na potezu, koji je upoznat sa optimalnom strategijom, trenutna pozicija garantuje pobedu, ona se naziva bezopasnom ili dobijenom (skraćeno DP – dobijena pozicija), u protivnom je opasna ili izgubljena (skraćeno IP – izgubljena pozicija). „Nim” poseduje osobinu da se iz DP može preći u IP ili DP, ali iz IP bilo koji potez vodi u DP (za protivnika). Opisana situacija i omogućuje dobitnu strategiju koja se sastoji u nalaženju odgovarajućeg poteza (ne uvek jedinstvenog) koji svoju DP prevodi u protivničku IP.
Izložićemo sada kriterijum za DP koji je dao Čarls Buton. Neka je data početna pozicija 𝑃 = (𝑛1, 𝑛2 … 𝑛p), gde 𝑛ioznačava broj figura u i-tom redu. Napišimo svaki od brojeva u binarnom sistemu, recimo 11 = (1011)2, a zatim nađimo zbirove odgovarajućih cifara (koje se nalaze na istim pozicijama, dakle u istim kolonama) svih p binarnih brojeva, vršeći sabiranje u decimalnom sistemu. Neka najveći od brojeva 𝑛iima k cifara u binarnom sistemu, tada ćemo imati sume 𝑆1, … 𝑆k (videti tabelu 1). Nebitno je da li se sume označavaju s leva na desno, ili u obrnutom redu. Za početnu poziciju P = (3,4,5)imamo 𝑆1 = 2, 𝑆2 = 1, 𝑆3 = 2(tabela 1).

Tabela 1: pozicija (3,4,5) je neparna
Butonov kriterijum za bezopasnu poziciju DP glasi: pozicija P je bezopasna ako i samo ako je bar jedan od brojeva 𝑆1 neparan.
Na osnovu ovog, kriterijum za opasnu poziciju može se iskazati i na sledeći način: pozicija P je opasna ako i samo ako su svi zbirovi 𝑆1 parni brojevi.
Napomenimo da se u iskazanim kriterijumima nula smatra parnim brojem.
Obično se pozicija za koju su svi zbirovi 𝑆1 parni naziva parnom, u protivnom je neparna. U skladu sa prethodnim, parne pozicije su opasne (IP) za igrača na potezu, dok su neparne bezopasne (DP).
Dobitna strategija igrača koji ima DP zasniva se na sledećim tvrđenjima dokazanim, npr. u knjizi H. Štajnhauza One Hundred Problems in Elementary Mathematics (Dover Publication, 2016):
(i) Ako je pozicija P parna, bilo koji potez dovodi do neparne (DP) pozicije.
(ii) Ako je pozicija P neparna, uvek postoji potez koji dovodi do parne (IP) pozicije.
Igrač koji ima neparnu (bezopasnu) poziciju, svoju dobitnu strategiju sprovodi pomoću poteza kojim neparnu poziciju prevodi u parnu (prema ii takav potez uvek postoji). Njegov protivnik ne može preokrenuti igru u svoju korist jer bilo koji njegov potez dovodi do neparne pozicije (tvrđenje i).
Analizirajmo sledeća dva primera koristeći gornje kriterijume.
Primer 1. Posmatrajmo početnu poziciju P = (3,4,5) datu na slici 1. Ovoj poziciji odgovara tabela 1 iz koje vidimo da je neparna. To znači da u klasičnoj postavci igre „nim” (3,4,5) igrač koji počinje igru uvek dobija partiju ako do kraja igre pronalazi poteze kojim neparnu poziciju uvek prevodi u parnu. S obzirom da je jedino 𝑆2 = 1 neparno, dovoljno je iz prvog reda koji sadrži 3 figure uzeti 2 figure i od broja (11)2 = 3 (11) napraviti broj (01)2=1. Na taj način dobijaju se sume 𝑆1 = 2, 𝑆2 = 0, 𝑆3 = 2 i igrač na potezu ima parnu (IP) poziciju.
Dajemo primer igre između igrača A i B za početnu poziciju P = (3,4,5) (slika 1).
A: Uzima dve figure iz prvog reda. Dobija se pozicija (1,4,5) sa sumama (2,0,2).
B: Uzima jednu figuru iz 2. reda (pozicija (1,3,5), sume (1,1,3).
A: Uzima tri figure iz 3. reda (pozicija (1,3,2), sume (2,2)
B: Uzima jednu figuru iz prvog reda (pozicija (3,2), sume (2,1).
A: Uzima jednu figuru iz reda gde su tri figure (pozicija (2,2), sume (2,0).
Ovde bi igrač B mogao da preda partiju: ako uzme jednu figuru, A uzima dve, ako uzme dve, A uzima jednu: u oba slučaja ostaje samo jedna figura za gubitnika B. Partija se može predstaviti i pomoću sledećih slika, gde beli krugovi označavaju uzete figure.
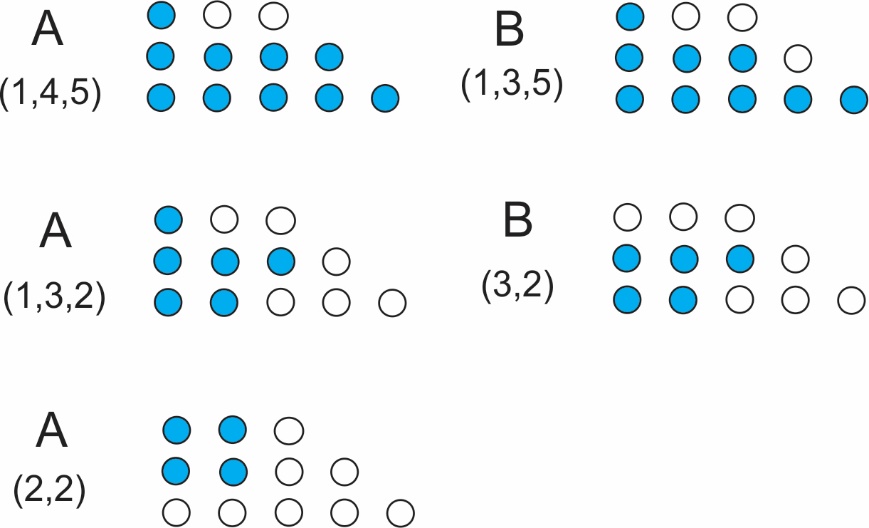
Primer 2. Za postavku nima sa slike 2 imamo P = (4,5,8,9) i na opisani način formiramo binarnu tabelu 2.
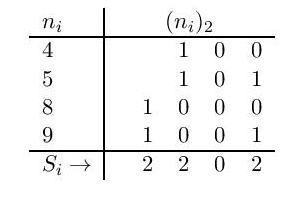
Tabela 2: pozicija (4,5,8,9)
Iz pabele 2 se vidi da je pozicija parna (opasna). Igrač koji je na potezu gubi partiju, ukoliko je njegov protivnik upoznat sa strategijom dobitka.
Primetimo da se igre u kojima postoji dobitna strategija u zavisnosti od rasporeda figura i od toga koji igrač povlači prvi potez svrstavaju u kategoriju nefer igara. Međutim, ovakva kategorizacija nije uticala na to da „nim” decenijama ostane popularna igra, čak je jedna partija viđena u filmu L’anné dernière à Marienbad (Poslednja godina u Marijenbadu), režisera Alena Renea iz 1961. (Marjenbad, naziv poznate banje u Češkoj na nemačkom jeziku, na češkom Marijanske Laznje).








Da li je šah „fer“ igra?
Pitanje je koliko zanimljivo toliko i staro, po prvi put se javlja krajem 18. veka. Zavisno od broja uzoraka i primenjene statističke metodologije, Beli ima prednost koja procentualno iznosi između 52 i 56%. Ovo se ne odnosi na početnike i brzopotezne partije već na vrlo renomirane profesionalce sa približno jednakim ELO rejtingom, a takođe i na kompjutere približno istih karakteritika u standardnoj partiji. Proizilazi da je šah skoro fer igra (ishod je najbiži remiju), što je i mišljenje bivših prvaka sveta Kapablanke, Laskera, Fišera i Kasparova. Više o ovoj interesantnoj temi može se naći na Wikipediji (First-move advantage in chess).