Пре више година на интернету је постављен веома популаран задатак о тежишту (центру гравитације) лименке пива стандардог облика ваљка. При испијања тежиште варира од центра лименке (почетак), спушта се према дну, а затим у неком моменту почиње да се враћа до центра (празна лименка). Ова варијација положаја тежишта доводи до интригантног питања: на којој висини од дна лименке се дешава преокрет?

Проф. др Миодраг Петковић
Овај кратак есеј посвећујем својим пријатељима, истакнутим професорима механике на Машинском факултету у Нишу, др Предрагу Kозићу и др Ратку Павловићу, који су преминули од короне у истој недељи 2021. године. Осим дубоко емотивног карактера, ова посвета носи и поруку да смо нас тројица заједно радили на решењу овог проблема који комбинује физику и математику.
Одговор на интернету дат је у облику теореме без доказа, тако је велики број посетилаца сајта тражио конкретан одговор. У овом прилогу бавимо се математичком теоријом положаја тежишта пива. У апстракту је дата формулација елементарног али изазовног задатка (довољно је средњошколско образовање) који је наишао на велики одјек како међу аматерима тако и међу универзитетским професорима, у доброј мери и зато што на сајту није дато решење. Ево текста тог задатка:
Пијете пиво из лименке (конзерве) облика ваљка. Kада је лименка пуна, тежиште (центар гравитације) лименке и пива заједно биће у центру лименке. Kада почнете да пијете пиво, центар гравитације се помера према доле али пошто се лименка испразни центар гравитације празне лименке је опет у центру. У којој је тачки (у односу на дно лименке) центар гравитације постигао минималну позицију?
Тачка у којој је центар гравитације достигао минимум назива се повратна тачка. Решење на интернету је дато у облику следећег тврђења без доказа:
Теорема. Висина повратне тачке (минимални положај центра гравитације) једнака је висини преостале количине пива у односу на дно лименке.
Добро, повероваћемо у тачност теореме која тврди да је минимални положај центра гравитације поклапа са површином преостале количине пива (разуме се, ниже од центра лименке). Међутим, и даље не знамо на којој висини се налази повратна тачка. Да бисмо добили конкретан одговор, кренућемо од основних појмова из физике и математике. Основни појам у геометрији маса је материјална тачка. Тачна позиција траженог минимума се може израчунати ако се знају висина лименке и тежине празне лименке и пива. Нека сукцесивне тачке P1, P2… Pn с масама М1, М2… Мn леже на истој правој L на растојањима D1, D2… Dn од произвољне фиксиране тачке О на правој L изван дужи P1Pn (слика 1).
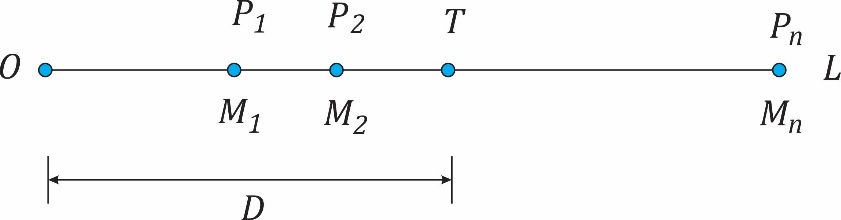
Сл. 1 Тежиште материјалних колинеарних тачака
Из физике је познато да тежиште Т материјалних тачака (центар маса) лежи на истој правој L на удаљености D од тачке О, при чему је D дато формулом
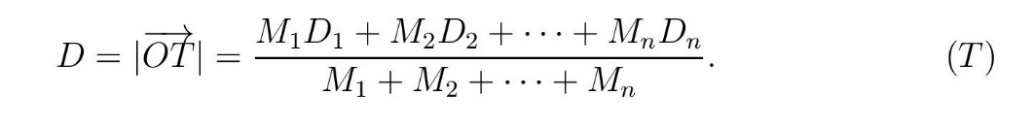
Напомена. У свакодневном животу маса се често замењује тежином, што је неисправно јер су то две различите физичке величине. Маса је мера тромости тела, док је тежина сила која зависи од гравитације; маса се изражава у килограмима [kg], а тежина у њутнима [N]). У константном гравитационом пољу, тежина објекта је пропорционална његовој маси, и таква употреба није проблематична; формула (Т) остаје у важности и за тежине због скраћивање константом пропорционалности. То не би важило негде далеко од Земље, али то је нека друга прича невезана за земаљске услове.
Нека је лименка прави цилиндар и усвојимо да флуид (пиво) „образује” такође прави цилиндар висине h и полупречника r. Нека је w1 тежина празне лименке а w2 тежина течности – у овом случају пива. Тежина пива у пуној лименки једнака је
![]()
где је s специфична тезина пива, а r полупречник лименке. Ако је ниво (висина) преосталог пива једнак x = th (t је број из интервала [0,1], t = 0 – празна лименка, t = 1 – пуна лименка), тада је нова тежина пива једнака
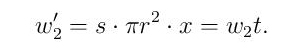
Посматрајмо лименку са пивом као јединствен објекат. Према формули (Т) (и узимајући у обзир напомену) центар гравитације (скраћено CG у наставку) је на висини
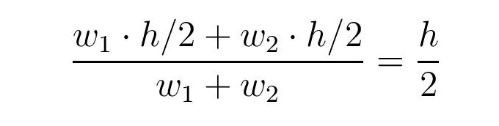
пре почетка испијања, што је и интуитивно јасно. Kако смо претпоставили да је попијена количина пива тежине w’2 = t · w2, на основу формуле (Т) следи да је нови CG на висини
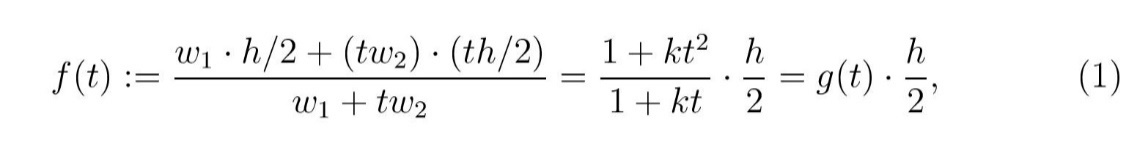
где је k = w2/w1 и g(t) нова функција. За произвољан позитиван број k лако је проверити да је g(t) < 1 на интервалу (0,1), што значи да је CG (жута тачка) увек испод половине висине лименке, изузимајући почетну (а) и завршну ситуацију (c). Ово је јасно и без горње математике (слика 2).
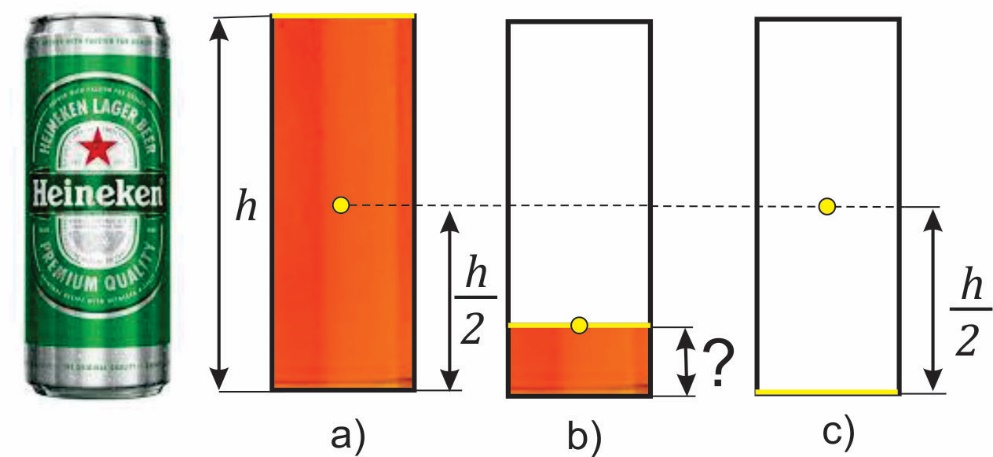
Сл. 2 Варијације тежишта лименке пива: а) пуна лименка, b) полупразна лименка и c) празна лименка
Да бисмо решили постављени задатак, прелазимо у домен математике, али то не треба да брине читаоца јер се ради о средњошколској елементарној математици, конкретније квадратним једначинама. Kратак подсетник: Kвадратни полином
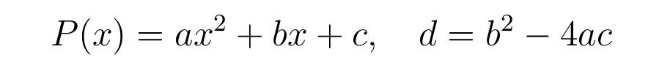
са дискриминантом d има два корена x1 и x2 (d > 0 или d < 0), или један двоструки корен, тј. x1 = x2 (d= 0) који су дати формулом
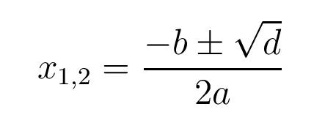
График квадратног полинома је парабола која (i) сече x-осу у две тачке (d > 0), (ii) не сече x-осу (d < 0) или (iii) додирује x-осу (d = 0, двоструки корен). У оном што следи потребно је одредити реалан број t* из интервала (0,1) за који функција g(t) достиже минимум. Типичан график функције g(t), нацртан за k = 10, приказан је на слици 3.
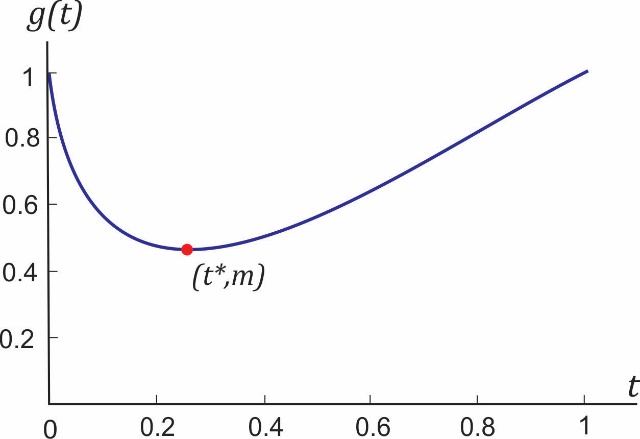
Сл. 3 График функције g(t) на интервалу [0,1] за k = 10
Минимум функције g(t) најједноставније је одредити коришћењем диференцијалног рачуна, али ми ћемо применити елементарну математику која се учи у основној школи или најкасније у средњој школи. Пре свега, приметимо да је
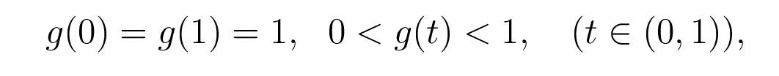
што је евидентно и са графика на слици 3. На основу ових чињеница и континуитета промене позиције тежишта, јасно је да мора постојати тачка (t*,m) у равни (t,g) таква да је
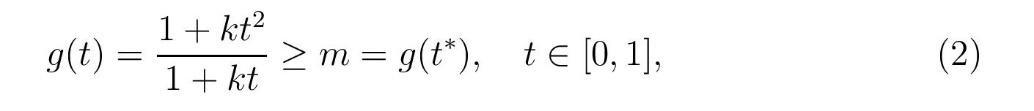
где смо са m (< 1) означили минималну вредност функције g на интервалу [0,1]. Очигледно да минимум функције g наступа ако се у (2) узме знак једнакости, што доводи до квадратне једначине по t
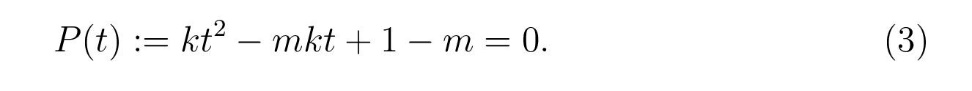
Kористећи формулу за решавање квадратне једначине, на основу (3) добијамо
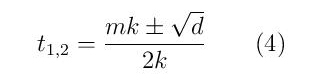
где је
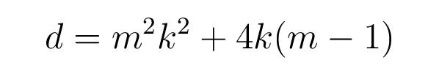
дискриминанта квадратне једначине (3). С обзиром на процес померања тежишта, померање од центра лименке према дну, достизање минимума и враћање у центар, решење квадратне једначине (3) има физичког смисла једино ако је јединствено. То значи да треба одбацити случајеве када се јављају два решења дата помоћу (4) (за d < 0 и d > 0) и изабрати јединствено решење које се добија узимајући d = 0 у (4). На тај начин долазимо до једначине
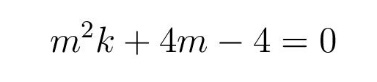
са решењима
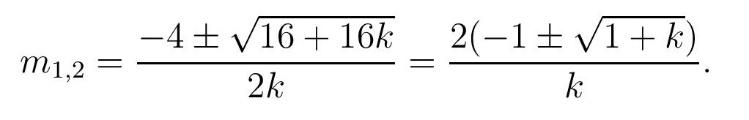
Kако је m позитиван број, одбацујемо негативно решење и добијамо минимум функције g(t)
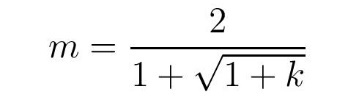
Из (4) (за d = 0) видимо да је t = m/2, тако да налазимо вредност аргумента t* која минимизира g(t):
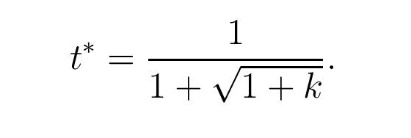
Овој вредности одговара тражена минимална висина x* = t*h. Из (1) добијамо тражену минималну висину CG:
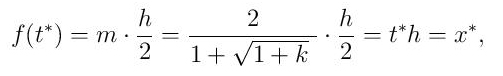
Овим смо доказали теорему из уводног дела овог прилога. Заиста, висина центра гравитације mh/2 поклапа се с висином x*= t*h преостале количине пива у односу на дно лименке.
Из последње формуле видимо да што је однос k тежине пива и тежине лименке већи, то је висина минималног CG нижа (и, наравно, испод половине висине h, f(t*) < h/2). На пример, за k = 10 добија се t*=0.231662… и g(t*)=0.463325… (што се може видети са слике 3), одакле је f(t) приближно 0.232 h.
У табели 1 је дата минимална висина CG за различите вредности односа тежина пива и празне лименке k, узимајући јединичну висину лименке h = 1.
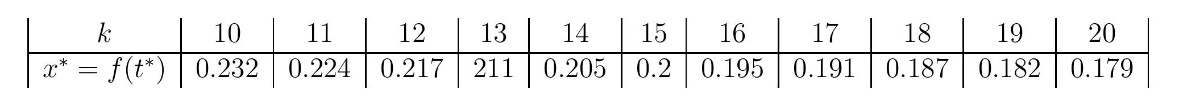
Табела 1








