Pre više godina na internetu je postavljen veoma popularan zadatak o težištu (centru gravitacije) limenke piva standardog oblika valjka. Pri ispijanja težište varira od centra limenke (početak), spušta se prema dnu, a zatim u nekom momentu počinje da se vraća do centra (prazna limenka). Ova varijacija položaja težišta dovodi do intrigantnog pitanja: na kojoj visini od dna limenke se dešava preokret?

Prof. dr Miodrag Petković
Ovaj kratak esej posvećujem svojim prijateljima, istaknutim profesorima mehanike na Mašinskom fakultetu u Nišu, dr Predragu Koziću i dr Ratku Pavloviću, koji su preminuli od korone u istoj nedelji 2021. godine. Osim duboko emotivnog karaktera, ova posveta nosi i poruku da smo nas trojica zajedno radili na rešenju ovog problema koji kombinuje fiziku i matematiku.
Odgovor na internetu dat je u obliku teoreme bez dokaza, tako je veliki broj posetilaca sajta tražio konkretan odgovor. U ovom prilogu bavimo se matematičkom teorijom položaja težišta piva. U apstraktu je data formulacija elementarnog ali izazovnog zadatka (dovoljno je srednjoškolsko obrazovanje) koji je naišao na veliki odjek kako među amaterima tako i među univerzitetskim profesorima, u dobroj meri i zato što na sajtu nije dato rešenje. Evo teksta tog zadatka:
Pijete pivo iz limenke (konzerve) oblika valjka. Kada je limenka puna, težište (centar gravitacije) limenke i piva zajedno biće u centru limenke. Kada počnete da pijete pivo, centar gravitacije se pomera prema dole ali pošto se limenka isprazni centar gravitacije prazne limenke je opet u centru. U kojoj je tački (u odnosu na dno limenke) centar gravitacije postigao minimalnu poziciju?
Tačka u kojoj je centar gravitacije dostigao minimum naziva se povratnatačka. Rešenje na internetu je dato u obliku sledećeg tvrđenja bez dokaza:
Teorema.Visina povratne tačke (minimalni položaj centra gravitacije) jednaka je visini preostale količine piva u odnosu na dno limenke.
Dobro, poverovaćemo u tačnost teoreme koja tvrdi da je minimalni položaj centra gravitacije poklapa sa površinom preostale količine piva (razume se, niže od centra limenke). Međutim, i dalje ne znamo na kojoj visini se nalazi povratna tačka. Da bismo dobili konkretan odgovor, krenućemo od osnovnih pojmova iz fizike i matematike. Osnovni pojam u geometriji masa je materijalna tačka. Tačna pozicija traženog minimuma se može izračunati ako se znaju visina limenke i težine prazne limenke i piva. Neka sukcesivne tačke P1, P2… Pn s masama M1, M2… Mn leže na istoj pravoj L na rastojanjima D1, D2… Dn od proizvoljne fiksirane tačke O na pravoj L izvan duži P1Pn (slika 1).
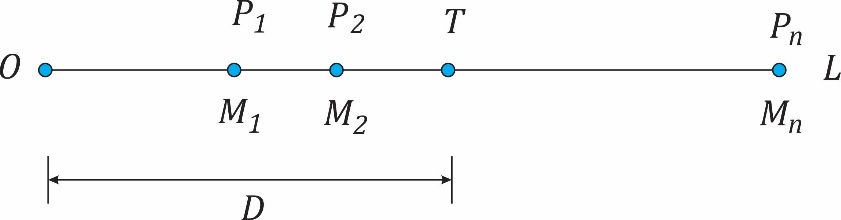
Sl. 1 Težište materijalnih kolinearnih tačaka
Iz fizike je poznato da težište T materijalnih tačaka (centar masa) leži na istoj pravoj L na udaljenosti D od tačke O, pri čemu je D dato formulom
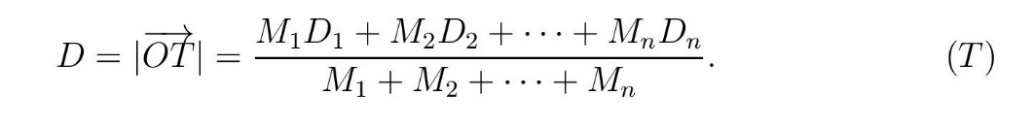
Napomena. U svakodnevnom životu masa se često zamenjuje težinom, što je neispravno jer su to dve različite fizičke veličine. Masa je mera tromosti tela, dok je težina sila koja zavisi od gravitacije; masa se izražava u kilogramima [kg], a težina u njutnima [N]). U konstantnom gravitacionom polju, težina objekta je proporcionalna njegovoj masi, i takva upotreba nije problematična; formula (T) ostaje u važnosti i za težine zbog skraćivanje konstantom proporcionalnosti. To ne bi važilo negde daleko od Zemlje, ali to je neka druga priča nevezana za zemaljske uslove.
Neka je limenka pravi cilindar i usvojimo da fluid (pivo) „obrazuje” takođe pravi cilindar visine h i poluprečnika r. Neka je w1 težina prazne limenke a w2 težina tečnosti – u ovom slučaju piva. Težina piva u punoj limenki jednaka je
![]()
gde je s specifična tezina piva, a r poluprečnik limenke. Ako je nivo (visina) preostalog piva jednak x = th (t je broj iz intervala [0,1], t = 0 – prazna limenka, t = 1 – puna limenka), tada je nova težina piva jednaka
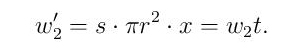
Posmatrajmo limenku sa pivom kao jedinstven objekat. Prema formuli (T) (i uzimajući u obzir napomenu) centar gravitacije (skraćeno CG u nastavku) je na visini
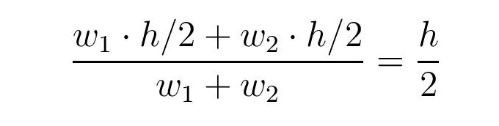
pre početka ispijanja, što je i intuitivno jasno. Kako smo pretpostavili da je popijena količina piva težine w’2 = t · w2, na osnovu formule (T) sledi da je novi CG na visini
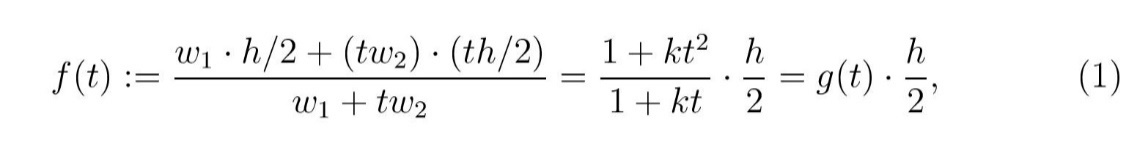
gde je k = w2/w1 ig(t)nova funkcija. Za proizvoljan pozitivan broj k lako je proveriti da je g(t) < 1 na intervalu (0,1), što znači da je CG (žuta tačka) uvek ispod polovine visine limenke, izuzimajući početnu (a) i završnu situaciju (c). Ovo je jasno i bez gornje matematike (slika 2).
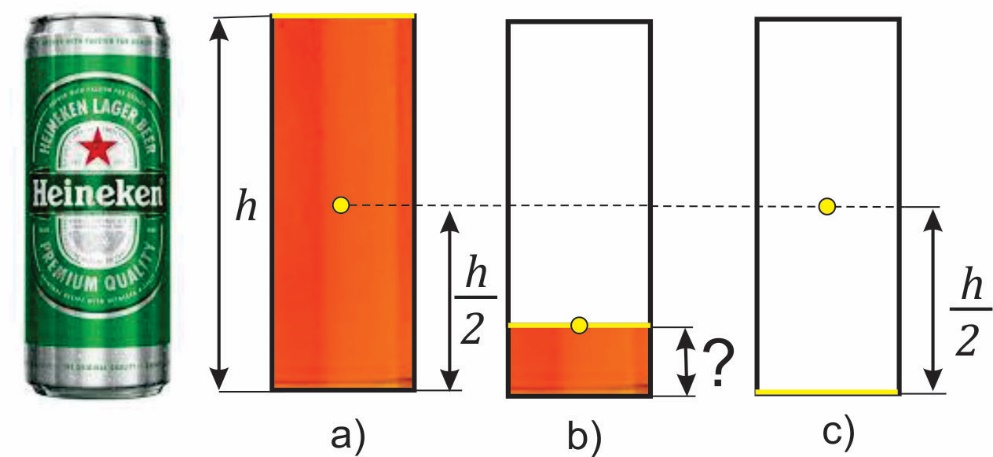
Sl. 2 Varijacije težišta limenke piva: a) puna limenka, b) poluprazna limenka i c) prazna limenka
Da bismo rešili postavljeni zadatak, prelazimo u domen matematike, ali to ne treba da brine čitaoca jer se radi o srednjoškolskoj elementarnoj matematici, konkretnije kvadratnim jednačinama. Kratak podsetnik: Kvadratni polinom
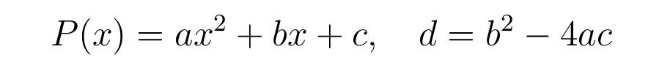
sa diskriminantom d ima dva korena x1 i x2 (d > 0 ili d < 0), ili jedan dvostruki koren, tj. x1 = x2 (d= 0) koji su dati formulom
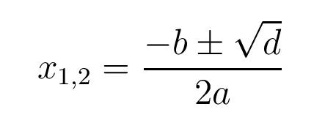
Grafik kvadratnog polinoma je parabola koja (i) seče x-osu u dve tačke (d > 0), (ii) ne seče x-osu (d < 0) ili (iii) dodiruje x-osu (d = 0, dvostruki koren). U onom što sledi potrebno je odrediti realan broj t* iz intervala (0,1) za koji funkcija g(t) dostiže minimum. Tipičan grafik funkcije g(t), nacrtan za k = 10, prikazan je na slici 3.
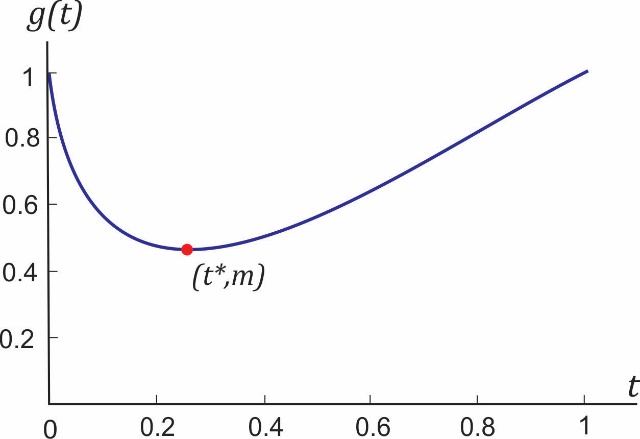
Sl. 3 Grafik funkcije g(t) na intervalu [0,1] za k = 10
Minimum funkcije g(t) najjednostavnije je odrediti korišćenjem diferencijalnog računa, ali mi ćemo primeniti elementarnu matematiku koja se uči u osnovnoj školi ili najkasnije u srednjoj školi. Pre svega, primetimo da je
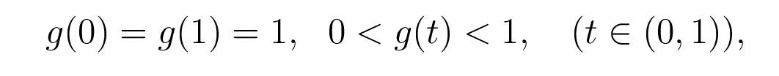
što je evidentno i sa grafika na slici 3. Na osnovu ovih činjenica i kontinuiteta promene pozicije težišta, jasno je da mora postojati tačka (t*,m) u ravni (t,g) takva da je
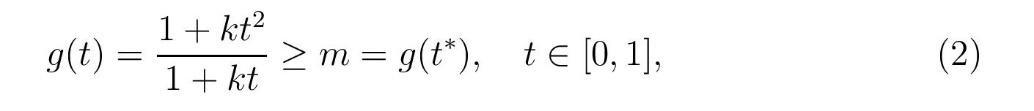
gde smo sa m (< 1) označili minimalnu vrednost funkcije g na intervalu [0,1]. Očigledno da minimum funkcije g nastupa ako se u (2) uzme znak jednakosti, što dovodi do kvadratne jednačine po t
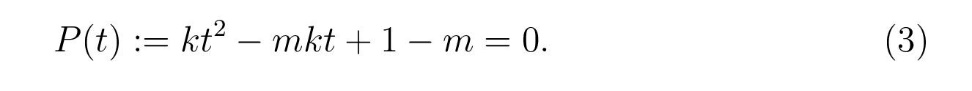
Koristeći formulu za rešavanje kvadratne jednačine, na osnovu (3) dobijamo
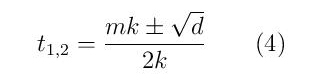
gde je
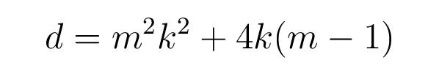
diskriminanta kvadratne jednačine (3). S obzirom na proces pomeranja težišta, pomeranje od centra limenke prema dnu, dostizanje minimuma i vraćanje u centar, rešenje kvadratne jednačine (3) ima fizičkog smisla jedino ako je jedinstveno. To znači da treba odbaciti slučajeve kada se javljaju dva rešenja data pomoću (4) (za d < 0 i d > 0) i izabrati jedinstveno rešenje koje se dobija uzimajući d = 0 u (4). Na taj način dolazimo do jednačine
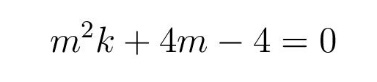
sa rešenjima
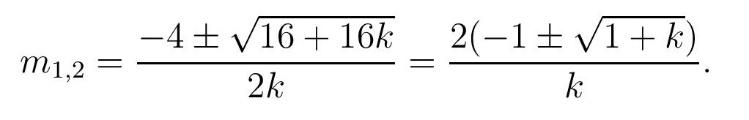
Kako je m pozitivan broj, odbacujemo negativno rešenje i dobijamo minimum funkcije g(t)
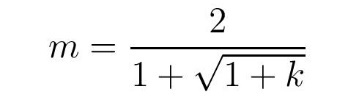
Iz (4) (za d = 0) vidimo da je t = m/2, tako da nalazimo vrednost argumenta t* koja minimizira g(t):
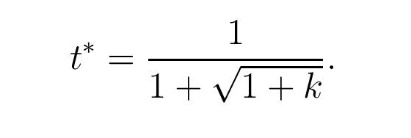
Ovoj vrednosti odgovara tražena minimalna visina x* = t*h. Iz (1) dobijamo traženu minimalnu visinu CG:
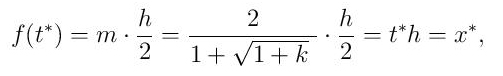
Ovim smo dokazali teoremu iz uvodnog dela ovog priloga. Zaista, visina centra gravitacije mh/2 poklapa se s visinom x*= t*h preostale količine piva u odnosu na dno limenke.
Iz poslednje formule vidimo da što je odnos k težine piva i težine limenke veći, to je visina minimalnog CG niža (i, naravno, ispod polovine visine h, f(t*) < h/2). Na primer, za k = 10 dobija se t*=0.231662… i g(t*)=0.463325… (što se može videti sa slike 3), odakle je f(t) približno 0.232 h.
U tabeli 1 je data minimalna visina CG za različite vrednosti odnosa težina piva i prazne limenke k, uzimajući jediničnu visinu limenke h = 1.
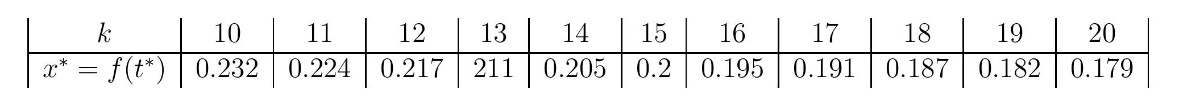
Tabela 1








