Matematički zadaci su još lepši i izazovniji ako se reše nekim nestandardnim metodom zasnovanoj na jednostavnoj ali sasvim neočekivanoj oštroumnoj ideji. U ovom prilogu prikazano je baš takvo rešenje zadatka koji ima i lepu priču, a autor je čuveni fizičar nobelovac Pol Dirak. Potreban nivo znanja – osnovna škola..

Prof. dr Miodrag Petković
U američkom dnevnom listu Saturday Evening Post oktobra 1926. pojavila se kratka priča B. A. Vilijamsa pod naslovom „Kokosovi orasi” o mornarima i kokosovim orasima na pustom ostrvu, koja je privukla veliku pažnju čitalaca.
„Pet mornara i jedan majmun pretrpeli su brodolom i uspeli da se domognu nepoznatog ostrva. Prvog dana su vredno sakupljali kokosove orahe. Uveče su mornari složili sve orahe, kojih nije bilo više od 20.000, na jednu gomilu i legli da spavaju ostavljajući za sutradan da ih ravnopravno podele. U neko doba noći, kada su svi zaspali, jedan od mornara se probudio i ustao.
Pomislio je da ujutru pri deobi oraha može doći do svađe, pa je odlučio da uzme svoj deo. Razdelio je sve orahe na pet jednakih delova, a jedan orah koji je preostao dao je majmunu. Zatim je sakrio svoj deo, a sve ostale orahe ponovo je stavio na gomilu.
Posle nekog vremena probudio se drugi mornar i uradio isto što i prvi. Kod njega je, takođe, ostao jedan orah i on ga je dao majmunu. I tako, jedan za drugim, postupili su i ostali brodolomnici. Svako je iz postojeće gomile uzeo petinu oraha, a preostali orah dao majmunu. Ujutru su podelili preostale orahe na pet delova. Opet je ostao jedan orah koji su dali majmunu. Razume se da su mornari primetili da je gomila koju su delili manja nego prethodnog dana, no kako je kod svakog savest bila nečista, niko ništa nije glasno primetio. Koliko je bilo kokosovih oraha u početku?”
Vilijamsova priča nije sadržala ono što je radoznalce mučilo – odgovor na pitanje koliko je bilo oraha? Izostanak rešenja uzrokovao je da je samo u toku prve nedelje od objavljivanja u redakciju časopisa stiglo oko 2.000 pisama u kojima su čitaoci, nemoćni da sami odgovore na postavljeno pitanje, tražili odgovor. Sledećih dvadesetak godina Vilijams je dobijao pisma čitalaca s novim rešenjima i predlozima za uopštavanje zadatka. I evo, prošlo je skoro sto godina, a zadatak o majmunu i kokosovim orasima ne gubi na popularnosti. Videti, na primer, knjigu Famous Puzzles of Great Mathematicians (American Mathematical Society, 2009) autora ovog priloga. Za razliku od Vilijamsa, autor ovog priloga neće ostaviti čitaoce „Galaksije” da se zbog vrlo vrućeg leta znoje dodatno i zbog rešenja ovog zadatka. Pretpostavimo da su mornari sakupili n (< 20.000) oraha. Neka je n1 deo koji je uzeo prvi mornar, a n2, n3, n4 i n5 delovi drugog, trećeg, četvrtog i petog mornara. Sa n6 označimo broj oraha koji je svako dobio pri zajedničkoj deobi. Tada se može formirati sledeći sistem jednačina:
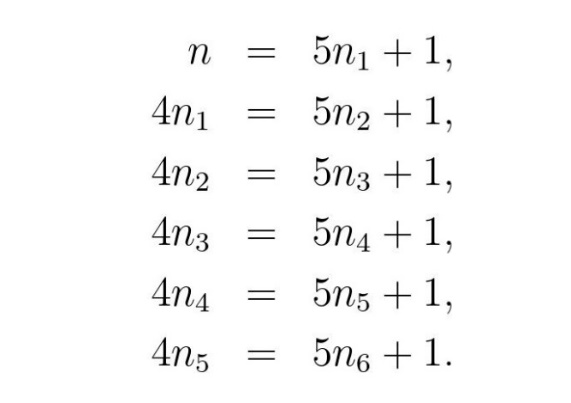
Jedinica koja se dodaje desnoj strani svake od jednačina odnosi se na orah koji dobija majmun. Sve nepoznate u gornjem sistemu su, razume se, prirodni brojevi.
Procesom eliminacije gornji sistem jednačina se svodi na jednačinu Diofantovog tipa
1024n = 15625n6 + 11529.
To je tip jednačina kod kojih se zahteva da rešenja budu racionalni ili celi brojevi. Podsećamo da je Diofant bio grčki matematičar koji je živeo u Aleksandriji u 3. veku.
Postoji nekoliko načina za rešavanja gornjeg problema. Najjednostavniji je primena Ojlerovog metoda koji se sastoji u snižavanju vrednosti koeficijenata u Diofantovim jednačinama dobijenim iz originalne jednačine. Međutim, to je rutinski metod i ne mnogo interesantan, tako da ćemo u ovom slučaju njegovu primenu ostaviti za neku drugu priliku. Umesto toga izložićemo jedno veoma elegantno rešenje koje se pripisuje čuvenom engleskom fizičaru Polu Diraku (Paul Dirac, 1902-1984), dobitniku Nobelove nagrade za fiziku 1933. (zajedno sa Šredingerom), naučniku koji je dao značajan doprinos kvantnoj mehanici i kvantnoj elektrodinamici. U literaturi se, mada dosta retko, pominje da autor rešenja nije Dirak već takođe čuveni atomski fizičar, „otac atomske bombe” i nobelovac Enriko Fermi (1901-1954).
Međutim, to i nije toliko važno za ovu priču, u centru pažnje je izvanredna ideja za rešavanje postavljenog zadatka, koja je toliko jednostavna da gotovo liči na trik, mada njen instruktivni aspekt svakako treba uvažiti. Uostalom, najjednostavnija rešenja često su i najbolja, najefikasnija, najelegantnija itd.

Pol Dirak (portret Clara Ewald)
Analizirajmo ukratko postavljeni zadatak. Potrebno je odrediti najmanji mogući broj M sa osobinama: (i) M je deljivo sa 5; (ii) razlika M – M/5 je, takođe, deljiva sa 5: (iii) opisani proces treba ponoviti šest puta uzastopce. Lako je naći da je 𝑀 = 56 = 15.625. Dodajući ovaj broj, kao i svaki njegov umnožak prirodnim brojem, bilo kojem broju koji zadovoljava uslove zadatka, dobićemo skup rešenja postavljenog problema iz koga treba izdvojiti rešenje koje daje broj manji od 20.000.
Izložimo sada Dirakovu ideju sa negativnim brojem oraha (?!). Neka je n = -4. Pokažimo, najpre, da ovaj broj zadovoljava uslove zadatka! Prvi mornar dolazi do gomile na kojoj su -4 oraha, daje jedan („pozitivan”) orah majmunu (svejedno je da li majmun dobija svoj orah pre ili posle deobe gomile oraha na pet delova). Na taj način, na gomili ostaje -5 oraha. Tu količinu mornar deli na pet delova, po -1 svakom. Zatim on uzima svoj deo, posle čega ostaju -4 oraha, dakle isto onoliko koliko je bilo na početku. Sledeći mornar sprovodi isti postupak s negativnim brojem oraha.
Posle svih „raspodela“ nepostojećih oraha svaki mornar će dobiti po -2 oraha (ovde je uključena i zajednička raspodela). U svemu tome dobio je jedino majmun i to šest (stvarnih) oraha. Da bi se našao odgovor potrebno je početnom broju -4 („kvazirešenju“) dodati broj 𝑘 × 56, (k = 1,2,…), pri čemu k treba izabrati tako da bude
-4 + 𝑘 × 56 = 15 625𝑘 – 4 < 20 000.
Očigledno je k = 1, tako da je traženo rešenje n = 15.621 oraha.
Izloženi prilaz rešavanju problema omogućuje nalaženje rešenja u opštem slučaju kada r mornara deli n oraha na r delova i za sebe uzima r-ti deo od postojeće količine oraha, dok preostalih m (< r) oraha daje majmunu. U slučaju 4 mornara startuje se sa -3m oraha i dodaje se broj 𝑘 × 45, u slučaju šestorice mornara polazi se od -5m oraha sa dodavanjem broja 𝑘 × 67 itd. U opštem slučaju dobijamo da je broj oraha na početku jednak
𝑘 × 𝑟𝑟+1 – 𝑚(𝑟 – 1)
(𝑘 prirodan broj), pri čemu se rešenje (ili rešenja) dobijaju za one vrednosti
k za koje gornji broj nije veći od n.









Umesto 56, 45, 67 mora da stoje stepeni 5^6, 4^5, 6^7. Verovatno je u pitanju tehnička greška.
Inace je prilog izvanredan.
U pravu ste Stevane, a greška je ispravljena. Izvinjavamo se prof. Miodragu Petkoviću i čitaocima Galaksije. Stanko Stojiljković