НОБЕЛОВАЦ БРОЈИ ОРАХЕ

Математички задаци су још лепши и изазовнији ако се реше неким нестандардним методом заснованој на једноставној али сасвим неочекиваној оштроумној идеји. У овом прилогу приказано је баш такво решење задатка који има и лепу причу, а аутор је чувени физичар нобеловац Пол Дирак. Потребан ниво знања – основна школа..

Проф. др Миодраг Петковић

У америчком дневном листу Saturday Evening Post октобра 1926. појавила се кратка прича Б. А. Вилијамса под насловом „Kокосови ораси” о морнарима и кокосовим орасима на пустом острву, која је привукла велику пажњу читалаца.

„Пет морнара и један мајмун претрпели су бродолом и успели да се домогну непознатог острва. Првог дана су вредно сакупљали кокосове орахе. Увече су морнари сложили све орахе, којих није било више од 20.000, на једну гомилу и легли да спавају остављајући за сутрадан да их равноправно поделе. У неко доба ноћи, када су сви заспали, један од морнара се пробудио и устао.
Помислио је да ујутру при деоби ораха може доћи до свађе, па је одлучио да узме свој део. Разделио је све орахе на пет једнаких делова, а један орах који је преостао дао је мајмуну. Затим је сакрио свој део, а све остале орахе поново је ставио на гомилу.

После неког времена пробудио се други морнар и урадио исто што и први. Kод њега је, такође, остао један орах и он га је дао мајмуну. И тако, један за другим, поступили су и остали бродоломници. Свако је из постојеће гомиле узео петину ораха, а преостали орах дао мајмуну. Ујутру су поделили преостале орахе на пет делова. Опет је остао један орах који су дали мајмуну. Разуме се да су морнари приметили да је гомила коју су делили мања него претходног дана, но како је код сваког савест била нечиста, нико ништа није гласно приметио. Kолико је било кокосових ораха у почетку?”

Вилијамсова прича није садржала оно што је радозналце мучило – одговор на питање колико је било ораха? Изостанак решења узроковао је да је само у току прве недеље од објављивања у редакцију часописа стигло око 2.000 писама у којима су читаоци, немоћни да сами одговоре на постављено питање, тражили одговор. Следећих двадесетак година Вилијамс је добијао писма читалаца с новим решењима и предлозима за уопштавање задатка. И ево, прошло је скоро сто година, а задатак о мајмуну и кокосовим орасима не губи на популарности. Видети, на пример, књигу Famous Puzzles of Great Mathematicians (American Mathematical Society, 2009) аутора овог прилога. За разлику од Вилијамса, аутор овог прилога неће оставити читаоце „Галаксије” да се због врло врућег лета зноје додатно и због решења овог задатка. Претпоставимо да су морнари сакупили n (< 20.000) ораха. Нека је n1 део који је узео први морнар, а n2, n3, n4 и n5 делови другог, трећег, четвртог и петог морнара. Са n6 означимо број ораха који је свако добио при заједничкој деоби. Тада се може формирати следећи систем једначина:

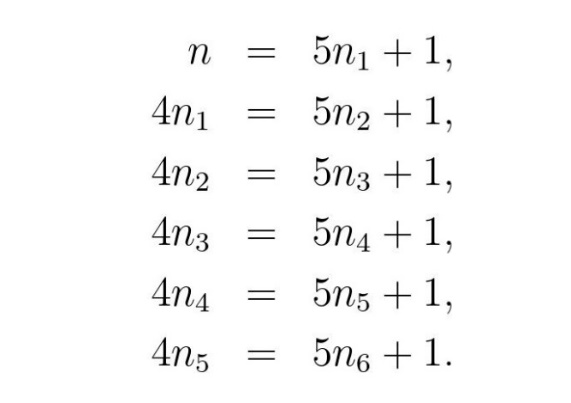
Јединица која се додаје десној страни сваке од једначина односи се на орах који добија мајмун. Све непознате у горњем систему су, разуме се, природни бројеви.

Процесом елиминације горњи систем једначина се своди на једначину Диофантовог типа

1024n = 15625n6 + 11529.

То је тип једначина код којих се захтева да решења буду рационални или цели бројеви. Подсећамо да је Диофант био грчки математичар који је живео у Александрији у 3. веку.

Постоји неколико начина за решавања горњег проблема. Најједноставнији је примена Ојлеровог метода који се састоји у снижавању вредности коефицијената у Диофантовим једначинама добијеним из оригиналне једначине. Међутим, то је рутински метод и не много интересантан, тако да ћемо у овом случају његову примену оставити за неку другу прилику. Уместо тога изложићемо једно веома елегантно решење које се приписује чувеном енглеском физичару Полу Дираку (Paul Dirac, 1902-1984), добитнику Нобелове награде за физику 1933. (заједно са Шредингером), научнику који је дао значајан допринос квантној механици и квантној електродинамици. У литератури се, мада доста ретко, помиње да аутор решења није Дирак већ такође чувени атомски физичар, „отац атомске бомбе” и нобеловац Енрико Ферми (1901-1954).

Међутим, то и није толико важно за ову причу, у центру пажње је изванредна идеја за решавање постављеног задатка, која је толико једноставна да готово личи на трик, мада њен инструктивни аспект свакако треба уважити. Уосталом, најједноставнија решења често су и најбоља, најефикаснија, најелегантнија итд.

Пол Дирак (портрет Clara Ewald)

Анализирајмо укратко постављени задатак. Потребно је одредити најмањи могући број М са особинама: (i) М је дељиво са 5; (ii) разлика M – M/5 је, такође, дељива са 5: (iii) описани процес треба поновити шест пута узастопце. Лако је наћи да је 𝑀 = 5⁶ = 15.625. Додајући овај број, као и сваки његов умножак природним бројем, било којем броју који задовољава услове задатка, добићемо скуп решења постављеног проблема из кога треба издвојити решење које даје број мањи од 20.000.

Изложимо сада Диракову идеју са негативним бројем ораха (?!). Нека је n = -4. Покажимо, најпре, да овај број задовољава услове задатка! Први морнар долази до гомиле на којој су -4 ораха, даје један („позитиван”) орах мајмуну (свеједно је да ли мајмун добија свој орах пре или после деобе гомиле ораха на пет делова). На тај начин, на гомили остаје -5 ораха. Ту количину морнар дели на пет делова, по -1 сваком. Затим он узима свој део, после чега остају -4 ораха, дакле исто онолико колико је било на почетку. Следећи морнар спроводи исти поступак с негативним бројем ораха.

После свих „расподела“ непостојећих ораха сваки морнар ће добити по -2 ораха (овде је укључена и заједничка расподела). У свему томе добио је једино мајмун и то шест (стварних) ораха. Да би се нашао одговор потребно је почетном броју -4 („квазирешењу“) додати број 𝑘 × 5⁶, (k = 1,2,…), при чему k треба изабрати тако да буде

-4 + 𝑘 × 5⁶ = 15 625𝑘 – 4 < 20 000.

Очигледно је k = 1, тако да је тражено решење n = 15.621 ораха.

Изложени прилаз решавању проблема омогућује налажење решења у општем случају када r морнара дели n ораха на r делова и за себе узима r-ти део од постојеће количине ораха, док преосталих m (< r) ораха даје мајмуну. У случају 4 морнара стартује се са -3m ораха и додаје се број 𝑘 × 4⁵, у случају шесторице морнара полази се од -5m ораха са додавањем броја 𝑘 × 6⁷ итд. У општем случају добијамо да је број ораха на почетку једнак

𝑘 × 𝑟^𝑟+1 – 𝑚(𝑟 – 1)

(𝑘 природан број), при чему се решење (или решења) добијају за оне вредности
k за које горњи број није већи од n.