У теорији вероватноће „парадокс рођендана” или „проблем рођендана”, познат и под називом „парадокс близанаца”, тврди да у групи од 23 случајно одабраних људи, шанса да постоји бар један пар особа који има рођендан истог дана, износи око 50 процената. Због овог неочекиваног исхода проблем се и назива „парадоксом рођендана”. У сварности, математички је све апсулутно коректно, осим изненађујућег решења тако да парадокса, у ствари, и нема.

Проф. др Миодраг Петковић
Повремено ће се под овим насловом у појављивати занимљиви прилози из света математике који укључују интересантне математичке формуле, догађаје из света математике и живота великих математичара, а и елементарне али интригантне и изазовне задатке за чије решавање је довољно средњошколско знање математике. Већина ових прилога, и још математичких прича и занимљивости може се наћи на сајту www.miodragpetkovic.com, аутора ових прилога (опције теме у менију).
Да не би дошло до забуне, напоменућемо да се у теорији вероватноће „парадокс рођендана” или „проблем близанаца” о коме ће бити речи, не односи на ефекат који се у литератури, такође, зове „парадокс близанаца” који има везе с временском дилатацијом као последицом теорије релативности. Подсетимо, ако један од двојице космонаута-близанаца путује ракетом брзином блиском брзини светлости, после извесног броја година проведеног у свемиру враћа се на Земљу знатно млађи него његов брат – путнику је време спорије протицало, тако каже Ајнштајнова теорија релативности. У нашој причи ради се о приземном догађају.
На забави се окупило велико друштво, свира музика и сви се лепо забављају, али вама је досадно. Онда сте се сетили да се мало раздрмате једном малом анкетом и кренете од особе до особе са истим питањем: којег датума у години имају рођендан? Kолико најмање особа треба да питате да бисте с вероватноћом од бар 50%, тј. већом од 1/2, добили исти одговор, тј. да међу присутним постоје бар две особе са истим рођенданом? Проблем је поставио амерички математичар (рођен у Аустрији) Рихард фон Мизес 1939.
Вероватно замишљате неки не тако мали број, рецимо 50 или 100, међутим, као што ћемо видети, тај број је 23. Због овог неочекиваног решења проблем се и зове „парадокс рођендана”. Решавајући овај проблем треба елиминисати преступну годину и претпоставити да се било који дан у години може појавити као рођендан, дакле с вероватноћом 1/365. Такође претпостављамо да на забави нема близанаца. Узгред да напоменемо да је према неким изворима иницијална каписла да фон Мизес формулише овај проблем била коинциденција датума рођења две славне личности: 12. фебруара 1809. рођени су амерички председник Абрахам Линколн и чувени енглески биолог Чарлс Дарвин.
Kако смо дошли до броја 23? Означимо с вероватноћу да две особе немају рођендан истог дана, а са P супротан догађај – две особе имају рођендан истог дана. Замислимо да су сви гости у дворишту и да, један по један, улазе у просторију за забаву. Потражимо вероватноћу да међу присутнима који улазе нема подударања рођендана. Kада прва особа уђе, вероватноћа да њен рођендан није исти као и неког од присутних је наравно 1 јер у просторији нема никог. То можемо да запишемо у облику разломка
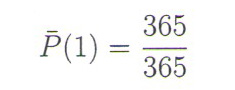
јер је бројилац 365 број свих повољних могућности, а именилац 365 је број свих могућих исхода.
Kада друга особа уђе, њен рођендан мора да буде различит од особе која је претходно ушла, тако да имамо 364 повољна избора од 365. Вероватноћа да ове две особе имају различите рођендане је
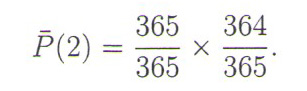
Kада трећа особа уђе, вероватноћа непоклапања рођендана за ове три особе једнака је
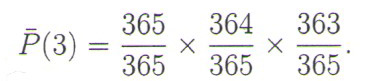
На основу претходног, начин израчунавања вероватноће различитих рођендана је јасан. После уласка k особа, вероватноћа за k различитих рођендана је
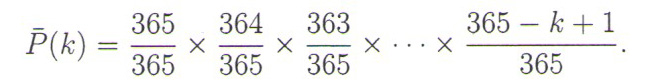
Вероватноћа да бар двоје присутних има рођендан истог дана једнака је супротној вероватноћи, тј.
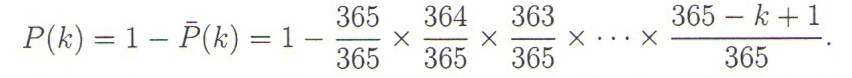
Да бисмо одговорили на постављено питање, потребно је пронаћи најмање k за које вероватноћа P(k) постаје већа од 1/2. Сваки од разломака у горњем производу, осим првог, мањи je од 1, тако да P(k) очигледно расте са порастом k и за неко к мора прећи границу од 1/2, видети слику у наставку прилога.
Прво k=k* за које је
![]()
даје тражено решење, где смо са P1/2 (n) означили критичну вероватноћу већу од 1/2 у случају n (теоријски) могићих исхода (365 дана). У нашем случају је k*=23 и добијамо
![]()
Приметимо да је P(22)=0.492703, дакле нешто испод 1/2. Према томе, тражени минимални број је 23. Дакле, можете се кладити са шансм од бар 50% да се међу 23 особе налазе бар две са истим рођенданом!
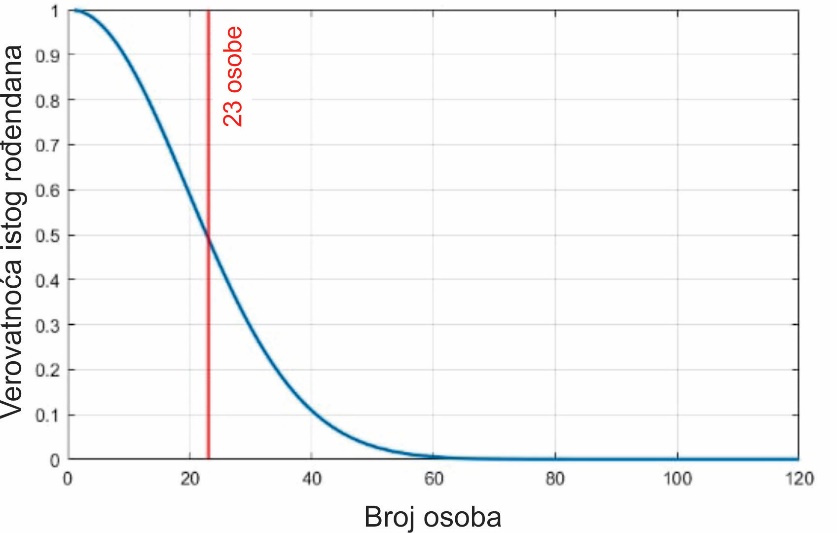
Добијени број изгледа заиста неочекивано мали, али не заборавимо да су овде у питању комбинације било ког пара особа међу присутним; ово је суштински различито од питања колико особа треба питати да би се утврдило с вероватноћом већом од 1/2 да неки од њих имају исти рођендан као нека конкретна особа, на пример баш ви. Одговор је знатно већи број – чак 253. На слици је приказана вероватноћа истог рођендана као функција броја анкетираних особа.
Занимљиво је напоменути да се дискутовани ефекат „близанаца” јавља код криптографских система који користе једну врсту тзв. хаш (hash) функција при трансферу порука. Ако би неки хакер покушао да дешифрује поруку коју је послао криптосистем користећи хаш функцију у 64-битном систему тако што би случајним избором дошао до n података, да би остварио свој циљ с вероватноћом не мањом од 0,5 било би му потребно око 1019 података (десет милијарди милијарди). Ако би хакер користио модеран PC (рецимо са „Интеловим” процесором i7 девете генерације), било ни му потребно око 1.000 година за овај покушај.
Анализа коришћена при разматрању „проблема рођендана” може се применити на ситуацију у којој неко слуша песме са MP3 плејера који садржи 1.000 песама. Ако плејер емитује песме случајним избором са списка (или како се то каже, плеј-листе), после колико песама са вероватноћом од бар 0,5 ће се поновити нека песма (не нека одређена, већ било која)?
Пре свега, рецимо да то зависи од тога шта се подразумева под „случајним избором”. Већина плејера или MP3 програма на рачунарима, мобилним телефонима и таблетима пакује песме са листе на исти начин на који се пакују (мешају) карте пре игре. Kада су једном спаковане, све песме се емитују редом и нема понављања све до 1.001 песме, дакле све док се листа од 1.000 песама не исцрпи. Ако се програм прекине опцијом „поновно паковање” (re-shuffling) и опет изврши паковање (shuffling), песме ће бити емитоване у неком другом реду, али опет без понављања.
Претпоставимо сада да имамо MP3 плејер и плеј-листу са 1.000 песама и да се свака песма бира случајно приликом сваког емитовања (тзв. suffleׅ или random опција). Kао у случају „парадокса рођендана”, после k песама вероватноћа да неће доћи до понављања неке од песама једнака је
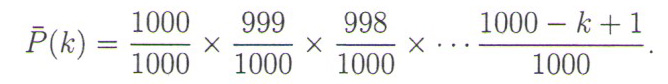
Супротна вероватноћа да ће се поновити бар једна песма са вероватноћом већом од 1/2 је
![]()
Очигледно је да вероватноћа P(k) расте с порастом k и опет тражимо најмање k=k* за које вероватноћа прелази 1/2. У нашем случају је k*=38 и добијамо
![]()
Приметимо да је P(37)=0,490464, дакле испод 1/2.
Може се показати (ову анализу прескачемо у овом прилогу) да је у проблемима које смо разматрали приближна процена за k* када постаје P(k*)>1/2 у случају великог броја n дата са
![]()
За разматрану плеј-листу од n=1.000 песама добија се на овај начин 37,23. Процена (у односу на тачну вредност k*=38) се може сматрати задовољавајућом јер је грешка само 2%.
Из ове приче може се закључити да је при решавању задатака из вероватноће веома важно схватити прецизно комплекс услова под којима се тражи вероватноћа реализације неког догађаја. Kао што је наглашено на почетку, догађај да две конкретне особе на некој великој забави имају рођендан истог дана у години је суштински различит од догађаја да бар две особе (било који пар) имају рођендан истог дана. За први догађај се може рећи да је врло редак, јер је вероватноћа да се деси прилично мала, док је други скоро обичан.
Следећи кратак прилог илуструје да редак догађај и те како може бити од изузетног, боље рећи, од животног значаја. Размотримо тврђење научника да је управо низ изузетно ретких догађаја и специфичних (погодних) услова довео до успона живота на Земљи. На пример, без протеина не би било живота на Земљи. Они се састоје од аминокиселина поређаних по одређеном редоследу. Kолаген, један тип протеина, представља ланац од 1.055 аминокиселина у тачно одређеном низу, а шанса да се то деси је 1/10260 (именилац се пише са 260 цифара). Kолико је то велики број поменимо да се процењује да у (тренутно) познатом свемиру има између 1078 и 1082 атома.
Скоро да се може закључити да по законима вероватноће протеини не би требало да постоје. Чувени астроном Фред Хојл је изгледе за формирање протеина упоредио с конструкцијом џамбо-џета од делова авиона насумично узетих са отпада. А ипак се чуда дешавају, у случају протеина то се зове чудо живота.








