Dok razgledamo (sliku ili statuu u galeriji, spomenik u parku itd.), zapažamo da postoji rastojanje s kojeg se posmatrani predmer najbolje vidi. To je privuklo pažnju velikog matematičara 15. veka Johana Milera (Johann Mller, 1436–1476), poznatijeg kao Regiomontan (Regiomontanus, Kraljevsko brdo). Značaj rada za nalažanje najboljeg vidika proističe iz činjenice da je to prva studija optimizacionog problema u matematici od antičkog doba. Danas ovo može rešiti svaki talentovani srednjoškolac.

Prof. dr Miodrag Petković
Johan Miler od Kenigsberga bio je nemački matematičar, astronom i prevodilac. Rođen je u Kenigsbergu (Kraljevsko brdo) u saveznoj državi Bavarska, tako da na srpskom jeziku njegovo ime glasi Jovan od Kraljevog brda. Milerov rodni grad ne treba mešati sa istoimenim poznatijim Kenigsbergom u Pruskoj, danas Kalinjingradom u Rusiji.
On se školovao u Lajpcigu, Budimu i Beču, a izvesno vreme proveo je putujući po severnoj Italiji prikupljajući matematičke i astronomske rukopise. Tada se upoznao s vodećim italijanskim matematičarima toga doba. Za to vreme je završio skraćenu verziju Almagesta pod nazivom Epytoma in almagesti Ptolemei. Almagest (2. vek n. e.) je Ptolomejov matematički i astronomski traktat kojim je predložen geocentrični model Sunčevog sistema (Zemlja u centru Sunčevog sistema). Almagest je najznačajniji izvor informacija o staroj grčkoj astronomiji. Smišljajući svoj revolucionarni heliocentrični sistem Nikola Kopernik je navodio ovu knjigu kao veoma uticajnu na svoj rad.
Johan Miler je 1474. u Nirnbergu sa svojim učenikom Bernardom Valterom napravio jednu od prvih kućnih astronomskih opservatorija u Evropi. Na teleskopu sopstvene izrade pratio je 59 dana kretanje komete vidljive godinu dana, počev od 1. marta 1471. (po julijanskom kalendaru), čak je pokušao (neuspešno) da odredi njeno rastojanje od Zemlje. U Nirnbergu je, takođe, odštampao u svojoj štampariji Efemeride – tablice položaja zvezda i planeta za svaki dan od 1474. do 1505, koje su zamenile zastarele Alfonsinske tablice. To su bile prve astronomske tabele u štampanom obliku koje su kasnije koristili Vasko da Gama, Kristifor Kolumbo, Fernando Magelan, Amerigo Vespuči i drugi istraživači. Smatra se da je Regiomontan bio najveći matematičar i astronom 15. veka. Jedan krater na Mesecu nosi njegovo ime.

Johan Miler (Wikipedia)
Rad na nalažanju najboljeg vidika smatra se prvom studijom optimizacionog problema u matematici još od antičkog doba. Regiomontan je ovaj problem postavio 1471. godine profesoru Kristijanu Roderu iz Erfurta. Problem maksimuma izložićemo u apstraktnoj geometrijskoj formi s nekim ograničenjima: on se jedino posmatra u ravni i posmatrani predmet je sveden na štap predstavljen vertikalnom duži.
Štap dužine d i zanemarljive debljine obešen je vertikalno na visini h od donjeg kraja do nivoa posmatračevog oka. Odrediti horizontalno rastojanje od vertikale obešenog štapa do oka posmatrača tako da se štap vidi najbolje.
Shodno pomenutim restrikcijama, konstruktivno rešenje biće u celosti predstavljeno u ravni. Najbolji vidik na posmatrani predmet biće kada vidni ugao BCA od posmatračevog oka (predstavljen tačkom C) prema štapu AB (pri čemu je |AB| = d) bude najveći (videti sliku 1), pri čemu oznaka |r| predstavlja dužinu duži r. Prava linija n, normalna na vertikalu (vešanja) OAB označava nivo pogleda.
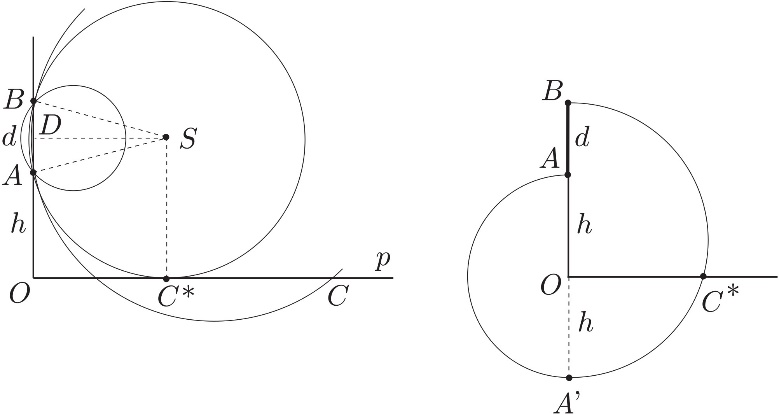
Sl. 1 i 2 Rastojanje najboljeg vidika
Nacrtajmo familiju krugova koji prolaze kroz tačke A i B (sl. 1). Vidni ugao, pod kojim se štap AB vidi iz neke tačke ravni, isti je za sve tačke koje leže na fiksnom krugu što pripada ovoj familiji (jer su periferni uglovi koji odgovaraju istoj tetivi datog kruga međusobno jednaki – jedna od osnovnih teorema u geometriji). Očigledno, ovi uglovi biće utoliko veći ukoliko je krug manji. Međutim, mi smo zainteresovani samo za tačke koje leže na pravoj p (nivo posmatračevog oka). Odavde sledi da ćemo do rešenja doći ako izaberemo tačku koja istovremeno leži na pravoj p i na krugu kroz A i B sa moguće što manjim poluprečniko m. Krug koji ispunjava ove zahteve očigledno je onaj koji samo dodiruje pravu p. Neka je C* tačka dodira tog kruga i prave p. Odavde nalazimo da je traženo rastojanje najboljeg vidika jednako x = |OC*|.
Kako naći rastojanje x = |OC*|? Neka je h = |OA| i |AB| = d (slika 2), tada je
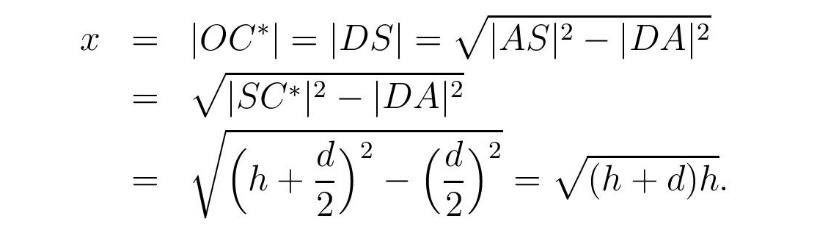
Prema tome, rastojanje optimalnog vidika je geometrijska sredina rastojanja gornjeg i donjeg kraja štapa od nivoa vidika. Kritična tačka C* može se naći pomoću geometrijske konstrukcije prikazane na slici 2, gde je |A’O| = |OA| = h i A’C*B polukrug prečnika |A’B| = 2h + d.
Kada znate kako odrediti rastojanje najboljeg vidika, neće vam biti teško (ako dođete dovoljno rano) da izaberete najpovoljniji položaj na grandioznom koncertu Rolling Stounsa (s visoko podignutom binom) s kojeg ćete najbolje videti omiljenog pevača Mika Džegera.

Koncert Rolling Stounsa, Ušće, Beogra, 2007. (M. Petković)
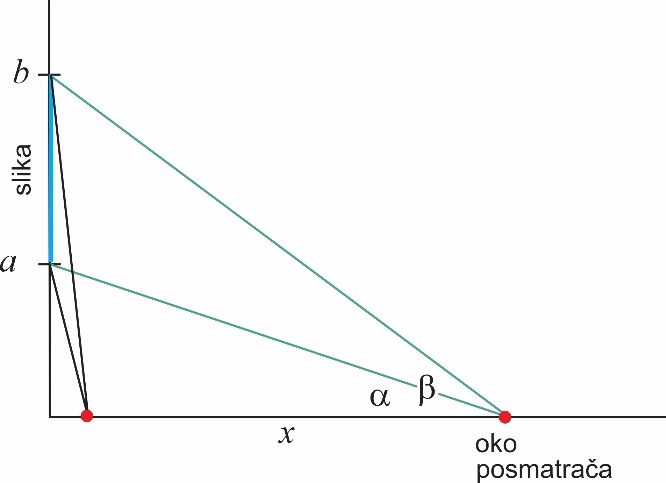
Sl. 3 Algebarsko rešenje Regiomontanovog problema
Problem optimalnog vidika može se jednostavno rešiti i algebarskim putem. Neka je a visina od posmatračevog oka do donjeg rama slike (plava boja), a b visina od posmatračevog oka do gormjeg rama slike. Dužina od posmatračevog oka do vertikalnog zida na kome je slika označena je sa x. Dalje, neka su α i β uglovi pod kojima se iz posmatračevog oka vide donja, odnosno gornja ivica slike (videti sliku 3). Da bismo dobili ugao najboljeg vidika od posmatračevog oka do slike, potrebno je maksimizirati razliku uglova β – α. Tangens ovog ugla raste s porastom njegovim na intervalu od 0 do 90 stepeni (slika 4).
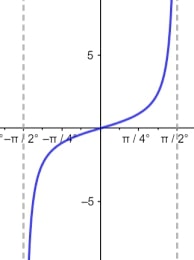
Sl. 4 Grafik tangens funkcije
Odavde proizilazi da treba maksimizirati
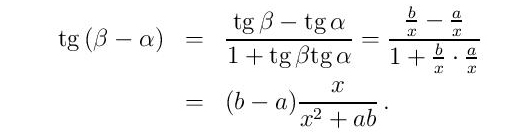
Kako je razlika b – a pozitivna, dovoljno je minimizirati recipročnu vrednost
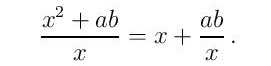
Jednostavnim algebarskim manipulacijama dobijamo
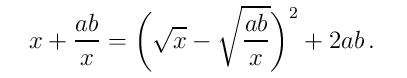
Odavde je jasno da će desna strana imati maksimum ako je kvadrirani izraz jednak nuli, odakle dobijamo
![]()
Ovo je isti rezultat koji smo prethodno dobili samo s drugačijim oznakama.
Dejvid Vels u svojoj knjizi The Penguin Book of Curious and Interesting Puzzles (Penguin Books, London 1992) analizirao je sledeću varijantu problema najboljeg vidika od praktičnog interesa.
Slika 4 prikazuje deo igrališta za ragbi (američki fudbal) s linijom gola g koja prolazi kroz stative gola A i B označene crnim kružićima i linijom normale n upravne na liniju gola. Prema pravilima ove igre, jedan od načina da se poentira jeste upućivanje lopte s normale n na gol (tzv. konverzija). Očigledno da je najbolja pozicija za konverziju određena tačkom T na liniji normale iz koje se gol AB vidi pod najvećim uglom.
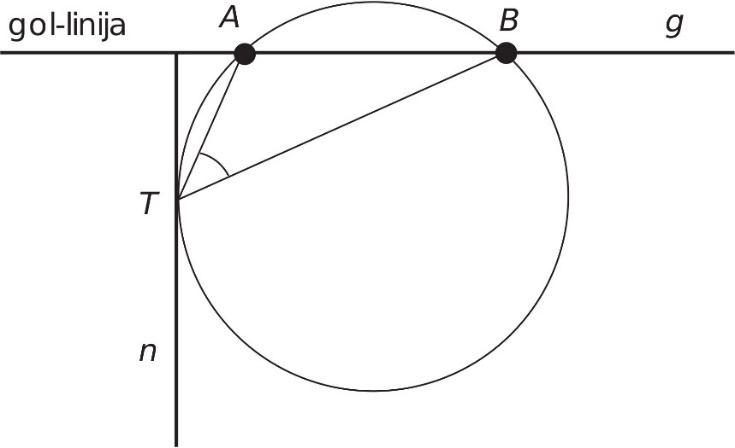
Sl. 5 Najbolja pozicija za konverziju u ragbiju
Podsećajući se prethodno razmatranog zadatka, jasno je da se rešenje ragbi problema svodi na rešenje Regiomontanovog problema najboljeg vidika. Konstruišući krug tako da prolazi kroz tačke A i B (stative gola) i dodiruje liniju normale n, nalazimo tačku dodira T koja određuje najbolju poziciju za konverziju jer se iz nje gol AB vidi pod najvećim uglom.
(Ilustracija: foto i redizajn Vladimir Petković)








